反求工程过程中基于NUBRS理论的轮廓光滑处理

张学栋，孙 宁

（桂林电子科技大学机电工程学院，广西桂林 541004）

反求工程中的重构过程，是首先利用可靠的实验方法测量出实体体数据场，有质量分布的坐标位置数值取1，没有质量分布的坐标位置数值取0。其次，用体素填充数值为1的坐标位置，用这种堆积的方法，构造出实体的粗糙模型。最后，用曲面构造技术光滑实体的轮廓表面，使构造的实体最终模型最大程度地再现实体原形。目前，反求工程的难点和研究重点，就在于实体轮廓的光滑处理。本文着重阐述了利用目前国际最流行的基于非均匀有理B样条理论的蒙皮法构造曲面的过程。

1 三维实体体数据场的获得

任何一个三维空间，都可以离散成有限的单元体集合，这些单元体的信息集合，称作三维体数据场。该数据通常是三维离散数据，一般称为体数据。对于形状规则的、可以用数学表达式表示的实体，体数据来源可以用科学计算，借助于计算机软件来生成。对于形状不规则的、无法用数学表达式表示的实体，体数据的获得就只能用测量的方法。在反求工程中，大部分的体数据都需要用测量的方法来获得。本实验组利用以专利《一种测量三维为体轮廓的设备和方法》为理论基础的独创的三维测量装置，即基于浮力的测量系统来获得体数据。体数据在逻辑上被组织成一个三维的数组空间（如图1所示），每一个数组成员存储一个单元体信息，叫做体素（Voxel），每个体素都由层号、行号和列号数据结构构成。

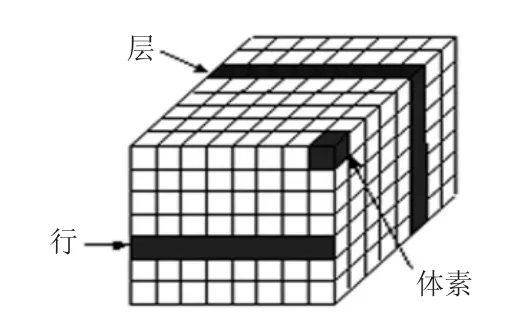
图1 体元素示意图

2 以立方体为体素重构实体

以立方体体素作为积木块，用空间位置枚举法来构造实体。用VB.NET语言编写程序[3]，调用Solidworks2007 API函数进行二次开发，来实现三维实体重构[1]。图2所示分别为重构的球体、圆锥体和三个半球槽[5]。

图2 球、圆锥和三个半球槽的重构示意图

3 光滑处理

由图2可见，由立方体体素构建的实体轮廓表面并不光滑，因此必须对实体轮廓表面进行光滑处理。

3.1 曲面构造法的比较

3.1.1 逆向反求工程中的曲面重构方法

曲面构造法的方法研究，一直是受到广泛重视的内容。通过测量数据建立产品表面模型或实体模型的方法有很多，根据不同的应用对象和应用场合，有不同的处理手段。按曲面模型的表达形式分类，逆向反求工程中的曲面重构方法大致可分为：

（1）三角Bezier曲面为基础的三边域曲面构造方案。三角区面以其构造灵活、边界适应性好及不受拓扑结构的限制的特点，在散乱点数据的曲面插值上起着重要作用。但绝大多数的CAD/CAM系统采用的是拓扑矩形曲面，因此用三角域的曲面重建方法与一般的曲面造型模块难以做到方法学上的统一，从而两者不兼容。

（2）以多面体方式来描述曲面物体。由于整个过程是自动进行的，使用较为简单方便，但其表达形式不为大多数CAD软件所支持，在此基础上，生成NURBS表面，才能进行后续处理。另外，这种方法不能精确地表示二次规则曲线曲面（如球体、圆柱等）。

（3）以B样条或NURBS曲面为基础的四边域曲面构造方案矩形域参数曲面拟合。矩形域参数曲面拟合方法，一直是曲面拟合方面的研究重点，应用对象主要是由复杂曲面组成的产品，如汽车、飞机、船舶等，这类产品既不是完全由简单二次曲面组成，也不像人脸那样毫无规律而言。矩形域曲面重构直接处理的数据是栅格数据，数据在空间拓扑形式为矩形。常用的曲面构造有Bezier、B样条(B-Spline)、NURBS等方法。其中，许多的研究成果己在CAD软件中广泛应用。

在逆向工程中，型值点数据(三维数据)具有大规模的特点，其B样条曲面的拟合有其自身特点。在B样条曲面拟合中，需研究的首要问题，是单一矩形域内曲面的散乱数据点的曲面拟合问题。在众多的研究中，Weiyin M和J P Kruth的工作较具代表性。他们首先根据边界构造一个初始曲面，然后将型值点投影到这个初始曲面上，接着根据投影位置算出其参数分布，从而解决散乱数据的参数分配问题。根据这一型值点参数分配拟合出一张新的NURBS曲面，然后再对型值点参数进行优化，使所拟合曲面离给定型值点误差最小。

3.1.2 矩形域参数曲面拟合的曲面重构方法

本研究的数据具有分层均匀规则特点，经过处理提取的边界体数据，仍然具有这一特点。综合分析三种曲面重构方法，结合本文处理的数据特点，选择矩形域参数曲面拟合方法。

矩形域参数曲面拟合方法的曲面重构主要有两种方法：

（1）先将测量点拟合成曲线，在通过曲面造型的方式，将曲线构建成曲面片；

（2）直接对测量数据拟合，生成曲面片，最终经过曲面的过渡、拼接和裁剪等曲面编辑操作，完成曲面模型的构建。

方法（1）以Solidworks软件中放样生成曲面为典型代表；方法（2）以UG中的点云拟合曲面为典型代表。本课题使用Solidworks三维设计软件作为开发平台，结合数据本身特点，选用方法（1）作为曲面构建方法。

3.2 NUBRS曲线和曲面[2]

曲线是构建曲面的基础，在逆向工程中，一种常用的模型重构，就是先将数据点通过插值或逼近拟合成样条曲线，再利用CAD造型工具如sweep、blend、lofting、四边曲面boundary等，完成曲面或曲面片造型。

NURBS用作计算，可以被计算机容易地处理，浮点错误相对稳定，对内存的需求相对较小，并且可以表示任何曲线和曲面.它是基于有理贝齐尔曲线的非有理B样条方法的推广。

非均匀有理B样条曲线定义为

式中，di为控制点；wi为权因子；Bi,k(u)(i=0，1，2…n)为K阶K-1次非均匀B样条。

该样条的基函数由下列递推公式给出

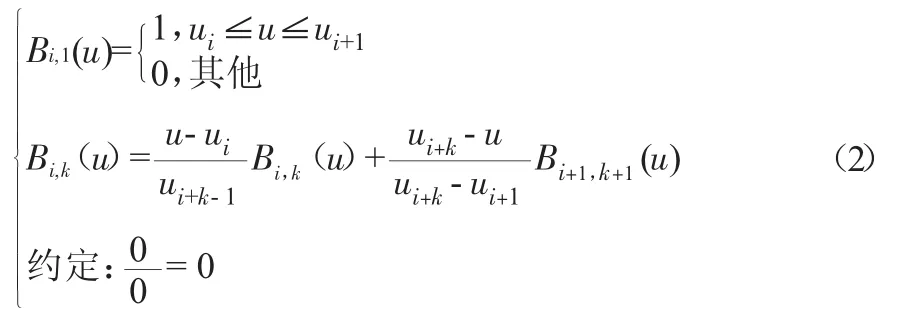
式中，节点矢量U=[u0+u1，…um]（m=n+k）；对于非周期的B样条，节点矢量两端去k重节点，即u0=u1=…=uk-1；um-k+1=um-k+2=…=um，以便曲线保持NURBS曲线的端点。

由于NURBS（Non-Uniform Rational B-spline即非均匀有理B样条）具有的各种优越性，它成为了STEP标准中制定的自由曲线曲面的唯一表示标准，为CAGD（Computer Aided Geometric Design计算机辅助设计）提供了统一的数学描述方法，并且在曲面造型中得到广泛的应用，成为目前CAD软件中描述产品几何形状的通用方法。

NURBS的曲面表达式如下：

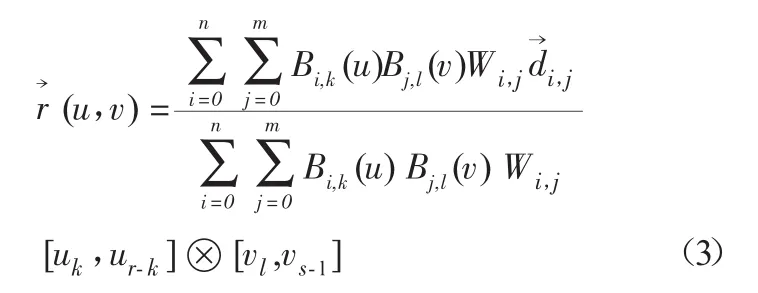
其中，沿u向和v向的节点矢量的节点数，分别为（r+1）和（s+1）（r=n+k，s=m+l）。

3.3 薄层轮廓数据点的提取与处理

曲线的构建十分重要，它是曲面构造的前提。构造曲线需要型值点，因此首先必须进行轮廓数据点提取。

对于单独一层薄片来说，每个体素就是一个正方体，从图3可以发现，薄层边缘轮廓点最多只有3个实孔单元体素与其相邻，内部点必然有4个实孔单元体素与其相邻，所以可以通过检测该层所有体素顶点的重合度，提取出截面轮廓点。

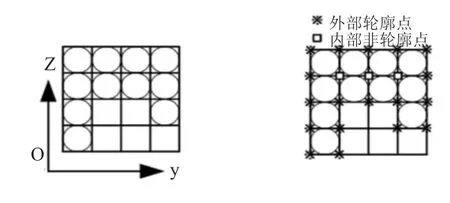
图3 边缘轮廓数据点的提取

利用插值法对提取的轮廓数据点进行曲线拟合。曲线插值法拟合曲线，就是令曲线通过所有测量点。这种方法的优点，是插值点的拟合误差为0，且不需要构造新的数据点来进行拟和，减小了数据量处理和因引入和删减数据带来的误差。一般在插值之前，要先去掉测量坏点，这也就是在数据处理时数据简化的目的所在[4]。插值法拟合曲线的流程图如图4。

图4 插值法拟合流程

4 曲面蒙皮构造NURBS曲面

蒙皮是传统的曲面生成领域中的常用方法，曲面的插值不再是通过给定的数据点阵，而是直接通过一簇曲线。其主要任务，是通过一组有序的称为截面曲线的空间曲线拟合的一张曲面，可形象地看成给一簇截面曲线构成的骨架蒙上一张光滑的皮。

用常规的NURBS插值方法进行曲面重构，需要求解大型的线性方程组，且重构曲面只能过插值点，计算复杂且存在不稳定现象。采用NURBS蒙皮技术，则可以通过所有的截面曲线（截形线），且将曲面拟合问题转化为两步曲线的拟合或插值问题，比较稳定，适合于截面数据构造曲面。

本课题研究中，根据Solid works曲线、曲面造型的特点，提出了利用角度对应引导线消除截面线对应型值点不对应产生的扭曲现象，角度对应引导线用3D样条曲线绘制，构建方法如下：

（1）先根据式（5），算出每一层的重心坐标；

（2）建立过以重心坐标横坐标为X轴、纵坐标为Y坐标的新坐标系。对于NURBS曲线同样进行坐标变换。对于每一层形成的NURBS曲线在新坐标系内，构造通过新原点（重心）的角度射线，必然会与之相交，这样可以求得交点。其中可以根据情况，选定射线每次转动角度。

（3）将每一层得到的对应角度的交点统一起来，这样可以避免出现扭曲现象。

（4）将求得的交点进行坐标转换，转换为初始坐标系内的交点坐标。

（5）求得的有序型值点方阵，为要求曲面的型值点，求出对应控制顶点方阵，即可满足型值点一一对应如图5(a)所示。

图5 角度引导线

利用Solidworks中3D草图绘制功能构造的对应的型值点连线，作为构造曲面的角度对应引导线。利用角度引导线，控制调整截面线起点（如图5a），生成圆柱体曲面（如图5b）可以消除曲面扭曲失真现象。

图6为图1重构实体经过蒙皮后的结果。

图6 光滑处理后的实体图形

5 误差分析

首先对圆锥斑马条纹，选取球形影射，对原始理想曲面、无引导线曲面、采用角度引导线的曲面分别进行条纹演示（如图7所示）。图7 a为理想模型斑马条文图，图7 b为未采用引导线重构模型斑马条文图，图7 c为采用4条引导线重构模型斑马条文图。从图中可以看出，采用引导线后，曲面斑马条文紊乱有所改善，说明采用引导线重构曲面光顺程度提高。

图7 斑马条纹图

剖切理想实体和构造实体，对得到的截面轮廓进行误差分析。本节以实心圆锥体为例，通过三种剖切面即过中心线斑马条文紊乱区域主剖、过中心线斑马条文规则区域主剖、平行于底平面的底剖进行误差分析。

平行于底面剖切误差分析方法：作平行于底面的平面剖切模型，在模型剖切截面上，以理论中心为直线端点，每10°绘制一条直线与截面轮廓线相交求取交点，利用测量模块测量每一个交点与理论中心点之间的距离并记录。通过与对理想模型进行同样剖切获得的理想标准数据相减，得出平行于底面剖切截面误差（如图8）。图中绘制了第20层和第30层两个截面误差图，从图中可以看出，截面最大误差约0.6 mm。

图8 平行于底面剖切误差图

过中心轴线剖切的误差分析方法：作过中心轴线的平面剖切模型，在剖切截面上，平行于底面绘制平行线，间距1 mm，求取平行线与截面轮廓的交点，测量每个点并记录，与理想模型值进行误差分析。

由图8可见，圆锥表面粗在斑马条文紊乱区域和相对规则区域，所以分别沿斑马条紊乱区域和相对规则区域，进行剖切误差分析（如图9）。从图9可以看出，斑马条文相对规则区域误差明显小于紊乱区域。

图9 过轴线剖切误差图

6 结束语

本文首先给出了由立方体体素重构的实体示例，接着介绍了目前流行的曲面构造方法和构造技术，采取适合本文的四边域NURBS法。在构造曲线之前，对于数据层进行轮廓数据点提取。接着详细介绍了NURBS曲线插值方法，采用均匀参数法构造曲线。传统蒙皮法可能出现层间数据点不对应、甚至曲面扭曲的现象，提出了角度对应引导线生成，来消除这方面对实体构造的影响。通过描述曲面编辑各种功能，选取了合适的功能来实现实体表面用曲面来代替，使得实体更加接近理想实体模型，最后给出了曲面蒙皮后的实体示例和误差分析。

[1][美]SolidWorks公司.SolidWorks高级教程二次开发与API[M].杭州新迪数字工程系统有限公司编译.北京：机械工业出版社，2009.

[2]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：高等教育出版社，2001.

[3]陈语林.Visual basic.NET程序设计教程[M].北京：中国水利水电出版社，2005.

[4]欧阳黎健.反求工程中预数据处理与模型修正[D].大连：大连交通大学，2006.

[5]任志伟.一种基于Solidworks三维规则点云数据场的重构方法[J].机械工程与自动化，2008，(4)：7-9.