基于可靠性技术的汽车钢板弹簧设计

赵建平

（南京理工大学紫金学院，江苏南京210046）

钢板弹簧作为影响车辆安全的重要零件之一，既负责传递所有各向力和力矩，还具有弹性元件、减振器和导向机构的特性，是重要的高负荷安全部件[1]。近年来，国内外学者对钢板弹簧的设计进行了研究。王其东[2]等利用虚拟样机理论，在整车动力学仿真的基础上，对汽车钢板弹簧的结构参数进行了优化设计，并对钢板弹簧进行了有限元分析；林开荣[3]利用模糊数学理论和优化设计方法，建立了基于模糊综合评判的汽车钢板弹簧优化设计的数学模型，并探讨了其优化设计方法；滕瑛瑶[4]等分析了弹簧材料、加工工艺、设计参数和使用条件对汽车钢板弹簧疲劳寿命的影响，为钢板弹簧的设计提供了一定的理论依据。上述文献中，可靠性设计在汽车钢板弹簧设计中的研究较少，而现今钢板弹簧可靠性日益受到关注，其设计和制造水平也提出了较高的要求。

1 可靠性设计基本理论和方法

所谓可靠性，是指产品在规定的时间内和给定的条件下，完成规定功能的能力。它不但直接反映产品各组成部件的质量，而且还影响到整个产品质量性能的优劣。事实上，可靠性设计所要解决的问题，就是如何从设计中入手，来解决产品的可靠性，以改善对各个零部件可靠度的要求，而可靠度的分配是可靠性设计的核心。零部件的载荷、几何尺寸、材料性能等都是随机变量，是某种概率分布的统计量。可靠性设计正是考虑设计参数的分散性，在常规设计公式的基础上，引入了可靠度或其他可靠性指标，不单纯用一个安全系数来衡量零件的强度，用概率统计的方法来处理各个设计变量，同时对系统失效的可能性进行定量分析和预测。

常规设计方法中，满足强度的判据为：零件的强度必须大于工作压力。可靠性设计的目标是：零件强度h大于工作压力S的概率，要大于或等于所要求满足的可靠度R。当已知概率密度函数或联合概率密度函数，且极限状态方程中的变量都是正态变量时，可靠性指标和可靠度很容易求得。若含有非正态变量时，只要进行等效正态变换，也容易求得可靠性指标和可靠度。但在工程实践中，往往很难有足够的资料来确定随机变量的概率密度函数或联合概率密度函数，而要确定它们的一阶矩和二阶矩(即均值、方差和协方差)却较容易，故可先求它们的一阶矩和二阶矩，再用二阶矩法求可靠性指标和可靠度[5]。

2 汽车钢板弹簧的可靠性设计

某型汽车钢板弹簧的已知参数如下：

钢板宽度（μb，σb）=（70，0.35）mm；

钢板长度（μl，σl）=（1 100，5.5）mm；

钢板弹簧厚度（μh，σh）=（6.5，0.032 5）mm；

车身载荷（μp，σp）=（5 537，276.85）N；

材料强度（μr，σr）=（614，45.8）MPa；

钢板片数n=6。

2.1 钢板弹簧的参数确定

（1）满载弧高fα。fa用来保证汽车具有给定的高度。当fa=0时，钢板弹簧在对称位置上工作。考虑到使用期间钢板弹簧塑性变形的影响，和为了在车架高度已限定时能得到足够的动挠度值，文中选取fa=15 mm。

（2）钢板弹簧长度L1。钢板弹簧长度L1是指弹簧伸直后两卷耳中心之间的距离。选用长一些的钢板弹簧，会在汽车上布置时产生困难。在总布置可能的条件下，应尽可能将钢板弹簧取长一些。文中L=1 100 mm，是包括卷耳及包耳边界的尺寸长度，所以L1=825 mm。

（3）钢板断面宽度b。有了钢板弹簧的平均厚度hp以后，再选钢板弹簧的片宽b。钢板弹簧的平均厚度hp可在下式计算得到。

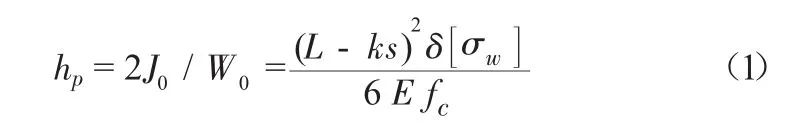
式中，U型螺栓中心距s为120 mm；

k为考虑U型螺栓夹紧弹簧后的无效长度系数，取k=0.5；

c为钢板弹簧垂直刚度（N/mm），c=Fw/fc；

δ为挠度增大系数δ=1.33；

E为材料的弹性模，E=2.1×105MPa；

代入式（1）中，求得hp=3.5 mm，b=70 mm。

（4）钢板弹簧片厚h。将计算得平均厚度hp=3.5 mm，代入式(2)，

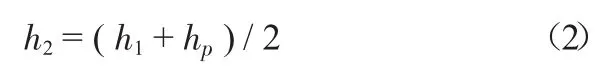
计算得厚度h2=5mm，为使各片寿命接近，又要求最厚片与最薄片厚度之比小于1.5，经验算，6.5/5=1.3＜1.5，验算合格。

（5）钢板弹簧各片长度。根据钢板弹簧长度计算公式：

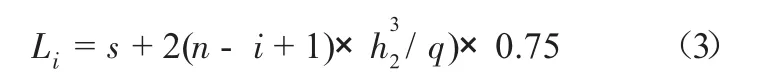
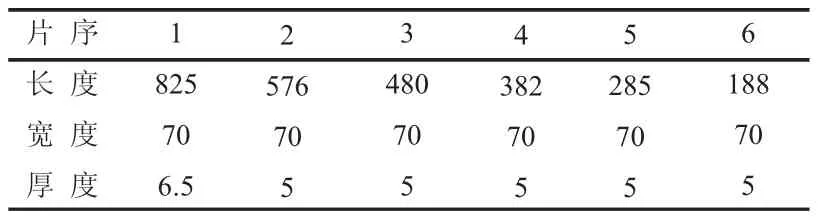
表1 各片钢板弹簧的基本尺寸单位：mm

2.2 可靠性设计

汽车的多片钢板弹簧，多半为中心受载的简支叠板弹簧，其工作应力为

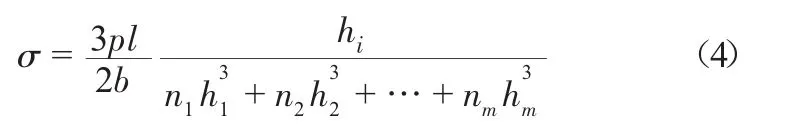
式中，p为载荷；几何尺寸宽度、厚度和跨距分别为b、hi和l；ni为钢板片数。

本文中，载荷 p=5 537 N，b=70 mm，h1=6.5 mm，h2=5 mm，l=1 100 mm，将hmax=7.3 mm代入式(4)，经过计算得 σmax=39.7 MPa。

根据应力—强度干涉理论，以应力极限状态表示的状态方程为

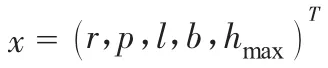
式中，r为钢板弹簧的材料强度；基本随机变量向量，其均值E(x)和方差及协方差Var(x)为已知，并且随机变量是服从正态分布相互独立。g(x)为状态函数，是反映钢板弹簧的状态和性能的，可表示钢板弹簧的两种状态：

g(x)≤0为失败状态；

g(x)>0为安全状态。

已知弹簧材料强度r=45.8 MPa，由式5计算得g(x)=r-σmax=45.8-39.7=6.1 MPa＞0，因此，钢板弹簧属于安全状态，可靠性验证成功。

把状态函数g(x)在随机变量向量x的均值E(x)=x軃处展开成二阶Taylor级数，根据的g(x)均值和方差的表达式，可求g(x)的均值和方差，然后再代入可靠性指标和可靠度的表达式，就能确定可靠性指标和可靠度。可靠性指标定义为

式中，μg为二阶近似均值，σg为一阶近似方差。

给定钢板弹簧的可靠性指标β=3.377，可查得可靠度R=0.999 6，根据加工公差和3σ法则，取钢板弹簧设计处的厚度h的标准差为σA，即可求钢板弹簧的最小厚度h的均值和标准差。

2.3 可靠性设计计算软件的开发

本可靠性设计计算软件在Windows XP中文系统环境下，采用面向对象程序设计语言工具Visual Basic进行开发。适用于普通汽车悬挂系统钢板弹簧可靠性设计与计算[6]。其程序流程图如图1所示。

汽车钢板弹簧可靠性设计计算软件应用的用户界面，如图2所示。它的生成依赖于其调用程序，可以直接输入所设计弹簧的基本悬挂指标。其中，已知满载质量为3.5 t，簧下质量为0.8 t，可靠性指标β=3.377，可靠度R=0.999 6，满载弧高fa=15 mm，板簧长度L=1 100 mm，板簧宽度b=70 mm；板簧片数n=6。点击“可靠性设计”，程序会计算出“板簧片厚h(mm)”和“各片长度 Li(mm)”，随后点击“可靠性验证”按钮，对设计计算出的数据进行验证，验证界面如图3所示。

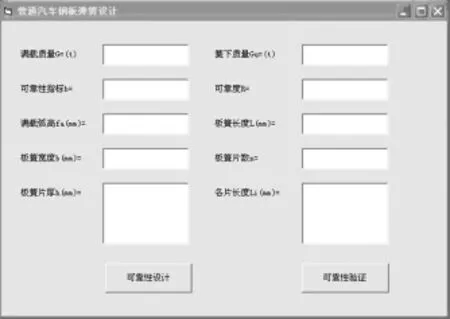
图2 用户界面图

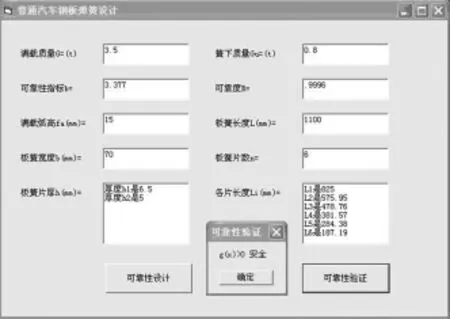
图3 用户验证界面

由图3可知，运用本文的软件设计计算方法，在满足可靠度要求的同时，精确计算出各钢板弹簧的厚度和长度，从而使钢板弹簧的设计计算较方便。数据输人快捷，数据存取容易，计算速度快，计算精度较高，能满足一般钢板弹簧可靠性设计计算要求。

3 结束语

随着汽车业界竞争的日益加剧，都在力求在保证产品质相短路故障持续0.1 s后切除，采用模糊控制的发电机端电压比采用传统PID控制的发电机端电压反应速度更快。

图7中实线部分为模糊控制的控制效果，虚线部分为传统PID的控制效果。如图7所示，发电机的角速度发生变化，三相短路故障持续0.1 s后切除，模糊控制能够使角速度变化量更快地回到零点，使系统稳定。

4 结束语

本文利用模糊控制对同步发电机进行控制，具有良好的励磁调节特性。模糊控制取代传统PID控制，可以有效地提高电力系统响应速度。通过仿真实验可以看出，在单机无穷大系统中，对于采用模糊控制的同步发电机，可以达到优于传统PID控制的效果，具有良好的前景。

[1]Wenxin Liu,G.K.Venayagamoorthy,and D.C.Wunsch.Design of Adaptive Neural Network Based Power System Stabilizer[J].Neural Networks，2003，(16)：891-898.

[2]Salman Mohagheghi,G.K.Venayagamoorthy,Ronald G.Harley.Adap tive Critic Design Based Neuro-Fuzzy Controller for a Static Compen sator in a Multimachine Power System[J].Power Systems，2006，(21)：1744-1754.

[3]王红君，赵 辉，华 岩．模糊参数自适应PID控制器在同步发电机励磁系统中的应用[J]．电气传动，2000，30(2)：37-40.

[4]乔志杰，王维庆．模糊自适应控制器的设计及其仿真[J]．控制系统，2008，(1)：26-29.

[5]韩唆峰，李玉惠．模糊控制技术[M]．重庆：重庆大学出版，2003．

[6]廉小亲．模糊控制技术[M]．北京：中国电力出版社，2003．