用移动元胞自动机法模拟杆式穿甲弹长细比对侵彻过程的影响*

黄德武,张 健

(沈阳理工大学装备工程学院,辽宁 沈阳110016)

1 引 言

连续介质力学以介质材料的连续假设为基础,包括流体力学﹑气体动力学﹑弹塑性力学﹑爆炸力学等。尽管各种物质都是由大量不连续的分子组成,但连续介质力学却不对物质的真实微观结构作深入探讨。这种假设给以牛顿微积分为基础的、要求变量处处连续可微的数学体系提供了应用可能。因为由这种假设推导出的结论一般都能满足工程需要,因此连续介质力学得到了广泛的应用,是最重要的力学方法。但近年来随着材料微、细观结构研究的最新进展,再用这种方法描述爆炸和高速穿甲时材料损伤﹑断裂和飞散的微观过程,有时会产生较大出入,不尽人意。

移动元胞自动机法是С.Д.Псахье等[1]在元胞自动机法[2]基础上发展起来的,它的主要特征是元胞不是固定在网格上变化,而是可以移动。MCA 假设材料由许多独立的元胞构成,元胞之间用“键”连接,“键”受冲击可断开,受强挤压时已断开的“键”还能重新连接,元胞间可以相对运动。元胞间的碰撞、挤压和摩擦可产生热量使元胞温度瞬间升高。用粒子力学方法对每个元胞对建立运动微分方程,在某个时间步长对所有元胞对的方程联立求解就得到一个“态”,下个步长又得到一个新“态”,将这些“态”连接起来,就完整描述了一个动态过程,这和生物细胞的复制、分裂及生物生长过程有些类似,因此称为元胞自动机法。不难看出,MCA 方法需要高速运算和超大规模存贮计算机。只有随着计算机硬﹑软件的发展及相关粒子力学理论的不断完善这种方法才能实现。MCA 方法对爆炸、穿甲、复合材料损伤、相变过程等问题的数值模拟是符合实际和有效的。本文中,对MCA 法作进一步的改进,增加了高速侵彻温度场的计算。

2 MCA 方法基本模型

2.1 元胞运动微分方程的建立

MCA 方法把被模拟的物体离散成一系列的微小单元,这些单元的位置不固定在某个网格上而是可以移动的,称为移动元胞,二维元胞可以是单层单元,物体内部任意相邻的两个元胞为一个元胞对。引入描述元胞对之间位置参数hij,并有如图1,hij为元胞对位移参数,rij为元胞i 的中心到元胞j 的中心的实际距离,rij,0为元胞未发生变形时、即两元胞相切时元胞i 到元胞j 的中心距离,di为元胞i 的直径。若两个元胞被拉开,则hij=rij-rij,0为正值,若互相挤压,则hij为负值,若定义hij为绝对值,即,则没有正负的符号问题。

图1 相邻元胞组成的元胞对Fig.1 A pair of the neighbor cells

在有限元法中,单元通过节点相连,节点在物理意义上是“绞链”。而在MCA 法中,元胞对位移参数hij,max类似可变形的“弹簧”,元胞之间的作用力与“弹簧”拉伸程度有关,一旦“弹簧”超过强度极限,元胞“键”就断开。显然,MCA 法比有限元法更接近实际。当hij＜hij,max时为连接状态,当hij＞hij,max时为断开状态。其中hij,max是元胞对位移参数的临界值,hij,max=rij,0εb,εb为材料断裂时的应变值,即材料的延伸率。这种方法的重要步骤是以任一个元胞对(i,j)为研究对象,建立两个元胞相互运动的平动和转动方程

式中:qij为从元胞i 的中心到该元胞与元胞j 接触后公共弦的距离;C(ij,ik)为与hij参数有关的系数;Ψ(αij,ik)为与ij、ik 等元胞对的相互排列角度参数αij,ik和泊松系数μ有关的变形系数;θij为元胞i、j 间的相对旋转角;τij为i、j 间的切向力;S(i j,ik)为与元胞对ij 和元胞对ik 的旋转角θ有关的系数;J i 为元胞i 绕质心的转动惯量。元胞对的变形见图2,位移参数见图3。

平动方程(1)中,左端第一项是元胞i、j 间的相对直线加速度,右端第一项是元胞i、j 间作用力pij引起的相对直线加速度,第二项是作用在i 元胞上、除了j 元胞外的其他邻近元胞作用力引起的加速度在i、j 方向上的投影,第三项是除了i 元胞外、作用在j 元胞上的其他邻近元胞的作用力引起的加速度在i、j 方向上的投影。转动方程(2)有类似意义,只是有关角加速度的。

方程(1)、(2)构成了两个元胞间相互作用的运动微分方程,当C(ij,ik)=1 或C(i j,j l)=1 且S(ij,ik)=1 或S(ij,j l)=1 时,可以转化为牛顿-欧拉运动方程

图2 元胞对间的变形Fig.2 Relative deformation of a pair

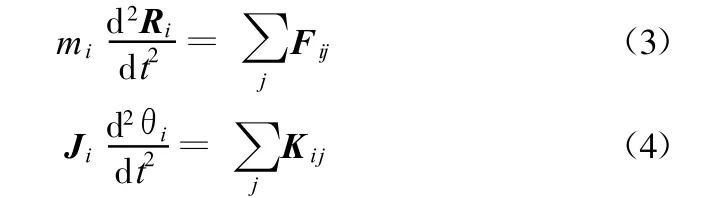
式中:Fij=pij+τij,Kij=qijnijτij,Ri、Rj是元胞i 和j 沿ij连线的位矢,模大小不等,nij是单位法向矢量,nij=(Rj-Ri)/(qij+qji)。

图3 元胞对位移参数Fig.3 Displacement parameters for the pairs

2.2 本构关系的构成

在MCA 方法中,整个试样本构关系由两部分构成,第一部分取决于每个元胞内部的应力应变关系,第二部分取决于元胞间的相互位置和元胞的运动状态。MCA 方法认定每个元胞内部应力和应变关系仍然遵循连续介质力学中的弹塑性小变形理论。一个试样内部元胞的数量是固定的,在冲击载荷作用下,受载荷直接作用的元胞间距离一般都缩短(试样被压实),同时各个邻近元胞受压缩后被激活和开始运动起来,具有一定的速度和加速度,开始时所有相邻元胞间都有“键”连接,受载后有些元胞间的“键”被拉断或被压断。既使不断,相互的连接力也随元胞运动的不同发生变化,这就决定了试样的承载能力和本构关系的不断改变。为了分析这两部分对试样本构的影响,先来研究单个元胞内的弹塑性变化。取一个元胞,周围元胞对它的作用可视为力和位移的边界条件,关系式为[3]

式中:如只考虑平面应力状态,则(α,β)=(x,y),σα和εα是应力和应变张量的对角分量;σav为平均应力,ταβ为剪切分量,K 为体积弹性模量,在各向同性弹性范围内,。φ为与元胞材料性质有关的乘子,φ=(2/3)dσint(εint)/dεint。其中

体积弹性模量K 是一个变量,因为在冲击引起的弹塑性变化中E 是随应变ε变化的。在原MCA 方法中,单个元胞内部应力和应变采用双线性强化弹塑性本构关系,E 的变化比较简单,只适应低速冲击,改进后的MCA 方法采用指数强化规律或二次强化规律

式中:ε是应变;E0是材料的弹性模量;E 是变形后材料的弹性模量;α是材料参数,由实验确定。

对于元胞对之间的正应力及切向剪应力,有

一个试样由很多元胞组成,每个元胞对的运动微分方程都可用式(1)～(2)描述,这样编制程序很方便,就象在有限元法中计算单元刚度矩阵一样,一个统一式适用于所有单元。然后再把所有元胞对运动方程联立起来,这又和有限元法中组集总体刚度矩阵类似,即在整体上表示了这个试样外载荷和形变之间的关系,也就是试样的本构关系。比较每个元胞内应力应变关系和元胞间位置及运动的变化对整个试样本构关系的贡献,可以发现后者是主要的,即前述的第二部分对试样本构关系贡献大。

2.3 元胞“键”的破坏规则

MCA 方法中,元胞之间是连接还是断开由元胞对位移参数hij决定,同时MCA 方法还采用等效应力作为判别元胞之间由连接到断开的判据

式中:σi,b为i 元胞的极限强度,K ij 为粘滞系数。满足式(7)或(8)时为断开状态。这就是说一个元胞对之间的“键”可以有两个破坏规则,变形过大被拉断或压断,相互挤压过重元胞“健”也被破坏。两个元胞间的“键”破坏以后,相互不再传递力的作用。如果一个元胞或一个元胞团(材料碎块)和周围元胞连接的“键”全部断了,这个元胞或元胞团(材料碎块)就脱离试样,游离或飞散出去。

当元胞i、j 为同一材料时,Kij=1;当元胞i、j 为不同材料时,K ij ≠1;K ij 表示两种材料界面的连接程度,可处理表面涂层、复合材料、不均匀介质等界面问题。如果任一材料元胞的等效应力满足破坏条件(7)或(8),不管另一种材料的元胞是否破坏,则元胞对之间的连接“键”断开,即界面开裂或脱离。如果界面的接合工艺不好,即界面连接强度低于基体内连接强度,则粘滞系数K ij 较小(K ij ＜1),即在较小的冲击载荷作用下,即可达到开裂条件。

2.4 元胞温度计算

实验表明,高速穿甲侵彻过程的时间很短,一般以微秒计。弹体撞击靶板瞬间,靶板和弹体头部的温度骤然升高,可能引起靶板材料局部熔化,高速穿甲温度效应不能忽略,但可视为绝热过程。在M CA 方法中,元胞i、j 之间作用力可分解为法向力和切向力

在冲击载荷下,冲击外力作弹性功转换成材料内势能,可以恢复,称有势力,冲击外力作塑性功不能恢复,转变成热量耗散,这部分称耗散力。因此

3 穿甲侵彻计算

弹芯材料为钨合金93W,材料参数分别为:密度ρ=17.5 t/m3,泊松比μ=0.33,弹性模量Ε=320 GPa,极限强度σb=2 GPa,断裂应变ε=0.04,比热容c=140 J/(kg·K),导热率λ=137 W/(m·K);靶板材料为27SiM nMo,材料参数分别为:ρ=7.8 t/m3,μ=0.28,E=206 GPa,σb=1.2 GPa,ε=0.08,c=450 J/(kg·K),λ=69.3 W/(m·K)。弹芯质量0.19 kg,靶板厚度300 mm,着靶速度1 km/s,依据模型中靶板的厚度和穿甲过程中靶板的破坏程度,靶板可看作半无限靶。模型中弹、靶元胞的尺寸相同,元胞的直径为1.7 mm。

穿甲弹芯长细比的设计对侵彻能力影响很大,选取长细比λ=L/D 分别为5、10、15、20、25 和30。弹芯质量相同,大长细比弹芯的直径必然小,弹芯具体尺寸见表1。

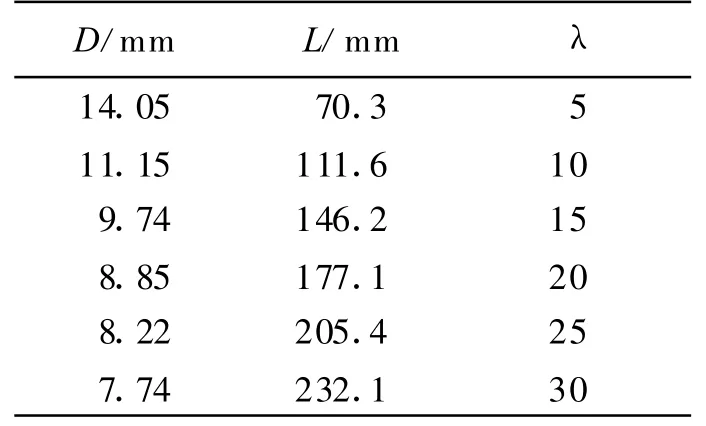
表1 杆式穿甲弹尺寸Table 1 The sizes of rod projectiles

图4 是长细比为10 的计算模型。模型的元胞总数为31 332,弹元胞总数325,靶元胞总数为31 007。

侵彻半无限靶的最后,或者弹体速度衰减为零,残余弹体嵌在靶板中,或者弹体质量耗尽,侵彻中止。图5 为长细比为10 的穿甲弹对靶板的侵彻过程。当t=87.5 μs 时,弹体长度消耗了2/3,速度下降为865 m/s,当t=125 μs 时,弹体长度消耗了9/10,速度下降为655 m/s,当t=225 μs 时,弹体质量消耗殆尽,侵彻过程停止。

图4 计算模型(λ=10)Fig.4 The model

图5 穿甲弹对靶板侵彻的破坏图(λ=10)Fig.5 The damage process of projectile to target

图6 为长细比为15 的弹芯在t=103 μs 时弹、靶的温度场。弹坑内侧温度比较高,弹坑底部已有一些元胞超过1 800 ℃(钢的熔点1 480 ℃),这和实验结果一致。通常在靶板弹孔内侧能观测到约10 μm 的白亮层,它是靶板材料被高速撞击和摩擦熔化后又快速凝固后形成的,称为熔化快凝层[4-5]。有人称穿甲侵彻过程为“熔穿”,即指弹、靶接触处由于高速冲击和强烈摩擦,瞬时可视为绝热过程,靶板弹坑底部温度能达到熔点。

图6 t=103 μs 时的温度场(λ=15)Fig.6 Temperature field at t=103 μs

在模拟侵彻过程中,弹头部和靶板相互受到的压力可达30 ～70 GPa。如果穿甲弹头部的表面元胞和弹体内部邻近元胞的连接“键”被全部压断,这些元胞就会飞散或移走。这样弹和靶板次表面的元胞就成为表面元胞,随着侵彻过程的进行,弹芯在缩短,靶板上的弹坑在延伸。弹、靶间的挤压应力通过元胞逐次传递以应力波的形式在弹体和靶板中向远处传播,应力波的传播速度远远大于穿甲弹芯侵彻靶板的速度,应力波的作用造成了远方元胞间“键”的破坏,形成了损伤区。图5 中弹、靶接触部分附近的白色区域均为损伤区,损伤区不规则是应力波反射和叠加的结果。图7 为t=87.5 μs 时弹体的放大网格图,节点代表元胞,节点间连线代表“键”。图中弹芯上部网格连接完好,每一个元胞与周围的六个元胞相连,形成正六边形排列;下部网格连接出现了不同程度的破坏,例如元胞30 473 与周围五个元胞的连接“键”已断开,若一个元胞的六个“键”全部断裂,则这个元胞将脱落和飞离,这意味着弹体质量在侵彻中不断消耗,这和实验结果符合。

图8 为质量和初速相同、长细比不同的杆式穿甲弹侵彻靶板的最大穿深曲线。从图中可以看出,随着长细比的增加,杆式穿甲弹的最大穿深逐渐增加。这是因为随着长细比的增大,由于弹芯质量不变,弹芯横截面上面积比动能变大,弹芯的侵彻能力增强,但当长细比超过25 以后,随着长细比的增加最大穿甲深度提高不明显,这和有些实验结果的结论非常吻合[6-7]。当然这里仅是从侵彻深度来讨论,杆式穿甲弹长细比过大,还应考虑膛内发射和碰靶时的弹体折断问题。

图7 弹体局部网格Fig.7 The zoom of the projectile

图8 最大穿深曲线Fig.8 The curve of penetrating depth

4 结 论

用MCA 方法对弹芯质量相同、长细比不同的钨合金穿甲弹侵彻靶板进行数值模拟,在着靶速度1 km/s 下,可以得出以下结论。

(1)用粒子力学的移动元胞自动机法模拟杆式穿甲弹芯侵彻靶板过程效果较好,弹、靶相互作用的细观破坏过程明显直观,弹坑形成、弹体质量消耗、弹孔温升均能很好描述。有利于分析穿甲过程的技术细节和更好进行穿甲弹与装甲防护的工程设计。

(2)长细比不同对半无限靶的最大穿甲深度也不相同,随着长细比的增加穿甲深度增加。长细比超过25 以后对穿甲深度影响较小,这和实验结果符合。

(3)弹、靶温度场的计算结果与实验观测值也比较一致,弹、靶接触处高速冲击和强烈摩擦,引起的靶板元胞温升可超过熔点,这和在靶场试验中观测到靶板弹孔内侧有熔化快凝层存在吻合。

[1] Psakhie S G, Stermeyer O G.Movable cellular automata method as a new tool in computational mechanics[J].Computational Materials Science,1999,16(4):333-344.

[2] von J Neumann.Theory of self-reproducing automata[M].Illinois:University of Illinois Press, 1966:157-162.

[3] 陈克,黄德武.用MCA 法模拟混凝土在冲击作用下损伤及破坏过程[J].兵工学报,2002,23(增刊):66-69.CH EN Ke, HUANG De-wu.Simulation of the damage of the concrete under the impact by movable cellular automata[J].Acta Armamentarii,2002,23(Supple):66-69.

[4] 黄晨光,董永香,段祝平.钨合金的冲击动力学性质及微细观结构的影响[J].力学进展,2003,33(4):433-445.H UANG Chen-guang,DONG Yong-xiang, DUANG Zhu-ping.Dynamic behaviors of tungsten alloy and its dependancwe on micro-and mesoscopic structures[J].Advanced in Mechanics,2003,33(4):433-445.

[5] 李金泉,黄德武,段占强.穿甲试验靶弹孔微观结构和绝热剪切带特性[J].北京科技大学学报,2003,25(6):545-549.LI Jin-quan, HUANG De-wu,DUAN Zhan-qiang.Mcrostructure near the penetrated hole in an experimental target and chracteristics of the adiabatic shear band[J].Journal of University of Science and Technology Beijing,2003,25(6):545-549.

[6] 王颂康,朱鹤松.高新技术弹药[M].北京:兵器工业出版社,1997:123-124.

[7] Anderson C E,Walker J D,Bless S J,et al.On the L/D effect for long-rod penetratiors[J].International Journal of Im pact Engineering,1996,18(3):247-264.