DCD 格式在破碎发射药床两相流内弹道计算中的应用*
2010-02-26贠来峰芮筱亭王国平
贠来峰,芮筱亭,王国平,陈 涛
(1.南京理工大学,江苏 南京210094;2.南京军事代表局,江苏 南京210024)
1 引 言
发射药床的挤压破碎是导致膛炸、膛胀等发射装药发射安全性问题的根本原因[1]。发射装药发射安全性数值模拟已成为发射安全性研究的世界性难题。在计算发射药床不同破碎程度对发射安全性的影响时,膛内发射药粒和燃烧气体运动的常用模型是一维非定常两相流[2-3]。若采用常用的Lax-Wendroff 格式和M ac Cormack 格式,为避免物理量梯度大造成计算不稳定而采用人工粘性或数值滤波,将使局部的破碎发射药被人为分散到较大的范围,导致计算结果严重“失真”。TVD 格式是20 世纪80 年代提出的一种高分辨率差分格式,具有较强的处理强间断的能力[4-5]。但在以往的两相流计算中,仅对气相采用TVD 格式,固相或液相仍采用M ac Cormack 或其他格式,不便编程[6-7]。若采用双流体模型,需要增加一个固相能量守恒方程[8],这种模型和方法对发射药粒为大尺寸颗粒的固体很难适用。因此,需寻求研究发射药床破碎对发射安全性影响的新的差分格式。
JIANG Zong-lin 等[9]结合Lax-Wendroff 和Beam-Warming 格式,提出了频散可控格式(DCS),该格式应用Steger-Warming 矢通量分裂技术,从修正方程的色散控制出发构造差分格式,利用格式的频散特性消除非物理振荡,无须人为附加粘性处理激波等强间断问题,具有格式简单、激波分辨率高、计算量小等优点,已广泛应用于爆轰波传播、反射过程的数值模拟[10-14]。JIANG Zong-lin 等[15]给该格式重新命名为频散可控耗散格式(DCD)。
本文中将DCD 格式引入内弹道两相流动力学计算,通过改写动力学方程组,实现用同一种格式对气相和固相统一处理。实例对某榴弹的内弹道进行数值模拟,模拟结果与实验结果吻合较好,表明数值模拟的正确性。并试图用DCD 格式和算法实现某穿甲弹发射药床破碎对发射安全性影响的数值模拟。
2 内弹道模型和方程

图1 中心点火装药结构Fig.1 Charge configuration with central ignition
一般火炮内弹道装药元件主要包括药筒、点传火系统和主装药。某中心点火发射装药如图1 所示。射击时,当底火被击发后,底火燃气射流喷入中心传火管,中心传火管内的点火药被逐步点燃,产生的燃气使中心传火管内的气体压力和温度不断上升,当压力达到破孔压力后,传火管上的传火孔被打开,点火气体从中心传火管流入主装药床中,点燃主装药药粒。当主装药被点然后,主装药燃烧气体使药室内的压力急剧上升,当压力达到一定值后,弹丸开始运动,药粒和燃气随之流入身管。药室内点传火过程中,燃烧气体流动受发射药颗粒的阻碍,造成速度和压力梯度,气固两相间的相互作用使药床中的药粒群产生疏密不均的分布,膛内压力差异使药床向弹底方向运动并在弹底堆积受到挤压,使各种波系在弹底反射形成反向压力梯度,药床因此又向膛底运动。在发射药燃烧全部结束之前,膛内气相和固相间总存在相互作用和相互运动,组成了膛内复杂的两相流动过程。
采用一维两相流内弹道计算方法处理膛内的两相流动问题,考虑的因素包括:质量、动量与能量的交换、气相和固相间的相互作用力、固相颗粒间的应力、弹丸挤进过程、弹丸在膛内运动中受到的阻力、中心传火管对炮膛截面变化的影响等。为研究方便,作基本假设如下:(1)主装药颗粒充分多并视药床为连续介质;(2)为使研究具有针对性,不考虑中心传火管的工作过程,把点传火系统工作结束时作为开始时刻,假设此时点火药燃烧气体在一定长度范围内平均分布,且无轴向速度;(3)膛内的流动是一维的,任一截面内的各处状态参数相等;(4)膛内物质只有气相和固相2 种,燃气组分不变,固相不可压缩,同一品号的药粒几何形状、尺寸和物性相同;(5)发射药燃烧服从几何燃烧定律和指数燃速定律;(6)燃气服从Nobel-Abel 气体状态方程;(7)忽略气体的粘性及对管壁的热散失;(8)忽略气相和固相间的热交换,把气体压力达到某确定值作为发射药粒被点燃的判据;(9)不考虑火炮的后坐运动。
在Euler 坐标下主装药的两相流体动力学基本方程组包括气相质量守恒方程、气相动量守恒方程、气相能量守恒方程、固相质量守恒方程、固相动量守恒方程。在写这些方程时,往往把与压力有关的项写在等式右边[3,6],以便采用Lax-Wendroff 和M ac Cormack 格式时,计算比较简洁,但采用TVD 格式时,有关固相的计算仍要采用M ac Cormack 或其他格式。为在两相中采用统一的差分格式,把与压力有关的项变形
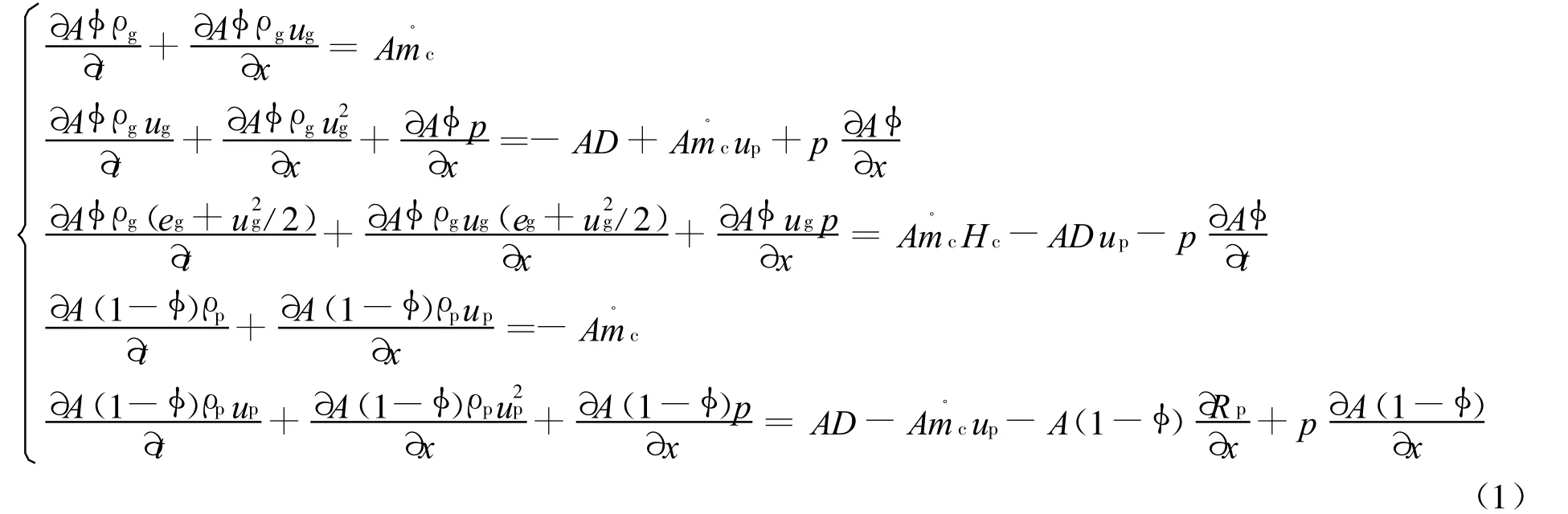
式中:A 为炮膛横截面积,φ为空隙率,ρg为气相密度,ρp为固相密度,ug为气体速度,up为固相速度,p为气体压力,eg为气体内能,D 为相间阻力,Rp为固相颗粒间应力,为定义在单位总体积上的主装药燃气质量生成速率,Hc 为单位质量主装药燃烧释放焓,R 为气体常数,T 为气体温度,γ为气体绝热指数,fp为发射药的火药力。
在求解式(1)的5 个守恒方程组成的主装药两相流动力学基本方程组时,需要用到Nobel-Abel 气体状态方程和弹丸运动方程

式中:α为燃气余容,mq为弹丸质量,uq为弹丸速度,As为弹带后断面处的炮膛截面积,为弹底气体压力,FR 为弹丸膛内运动阻力。
3 数值方法
经整理,把式(1)写为

采用DCD 格式离散式(4),得到显式差分格式如下[15]
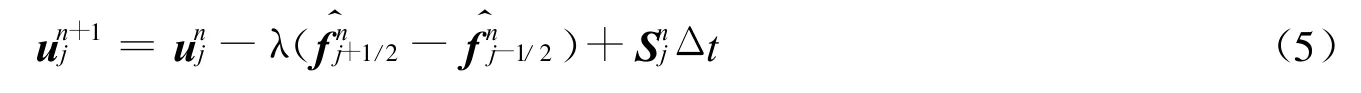
计算采用均匀分布网格。膛底为左边界,采用固壁条件。弹底为右边界,由于弹丸运动,右边界是移动边界。开始时把弹后空间分为J 个格子,每个格子的长度为Δx。当弹丸开始运动后,弹后的第1个格子,即第J 个格子是一个长度变化的格子,把移动的弹底总作为此格子的右边界。为处理方便,在此应用单元控制体方法建立控制体方程组,以求解右边界上的各物理参量。当该格子的长度大于2Δx时,取J=J+1,并对该格子重新赋值。
4 计算结果及其验证
某榴弹采用金属药筒,主装药为单一粒状硝基胍发射药,中心传火管为金属中心传火管。采用DCD 格式计算了该榴弹的内弹道两相流动力学。膛底最大压力pm 和弹丸炮口初速v0的计算结果为331.9 M Pa 和930.0 m/s,实验结果为327.4 M Pa 和931.0 m/s。图2 是膛底压力时间历程的计算与实验结果。由此可见,计算与实验结果吻合较好。
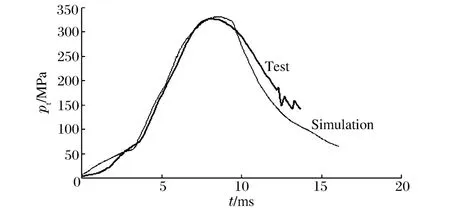
图2 膛底压力时间历程计算与实验结果Fig.2 Simulation and test results of breech pressure vs.time
5 发射药床挤压破碎对发射安全性的影响
大量实验证明,发射药床的挤压破碎尤其是在弹丸底部附近的破碎是导致膛炸、膛胀等发射安全性问题的根本原因[1,6,17-20]。在计算发射药床不同破碎程度对发射安全性的影响时,可假设破碎发射药床为具有不同破碎程度的几种发射药的混合装药结构,采用DCD 格式建立混合装药结构内弹道两相流动力学的算法,就可数值模拟发射药床破碎对发射安全性的影响。
挤压破碎后的发射药通常是不规则的,呈现各种各样的形状,而内弹道计算首先必须已知发射药粒的形状特征量,因此,无法直接对挤压破碎后的发射药进行内弹道计算。解决的办法有2 种:(1)从理论上建立发射药床的挤压破碎模型,直接计算它在膛内受挤压后的破碎程度,并得到相应的形状特征量;(2)通过发射药床的挤压破碎物理模拟实验获得挤压破碎后的发射药,然后通过测试其动态活度符合出相应的形状特征量。目前,在理论上建立准确的发射药床的挤压破碎模型计算破碎发射药床的药粒形状特征量还看不到希望。用第2 种方法获取药粒的形状特征量成为唯一的选择并有很好的可操作性。为处理方便,可把破碎发射药作为几种在平均意义下具有统一形状的一种新发射药,在计算中假设破碎后的每一种发射药为同一形状。
以某坦克炮穿甲弹(APFSDS)为对象,把挤压破碎后的发射药床看作由2 种发射药组成的混合装药结构,用DCD 格式对弹底附近的发射药床在不同破碎程度下的内弹道性能进行计算。表1 是膛底最大压力pm和弹底最大压力pm,d的计算结果。图3 是破碎方式1 ~4 下膛底压力时间历程的计算结果。图4(a)、(b)、(c)分别是破碎方式5、6、7 下膛内压力时间历程的计算结果,其中pt 表示膛底压力,pl 表示坡膛压力。

图3 破碎方式1 ~4 的膛底压力时间历程计算结果Fig.3 Computational results of breech pressure vs.time under fracture mode 1 4
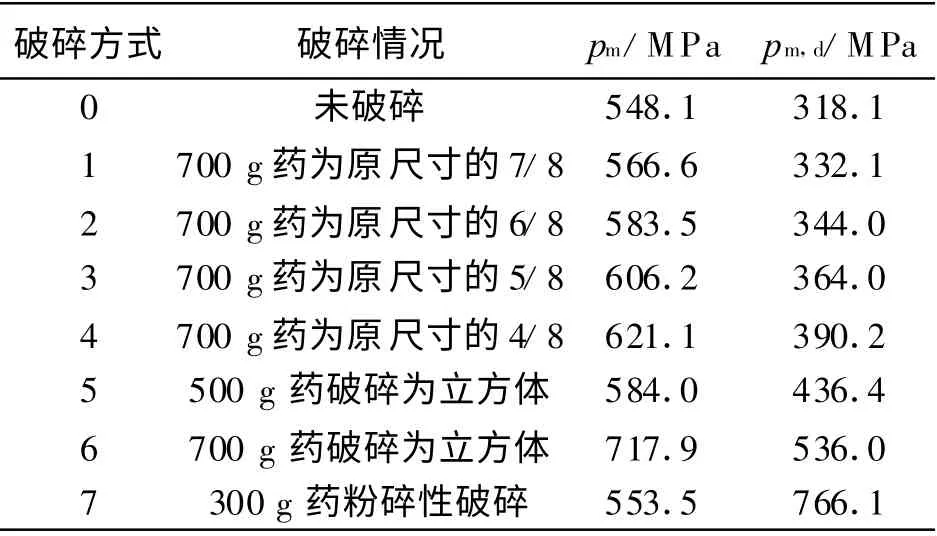
表1 发射药床破碎程度对发射安全性的影响Table 1 Influence of fracture degree of propellant charge on launch safety
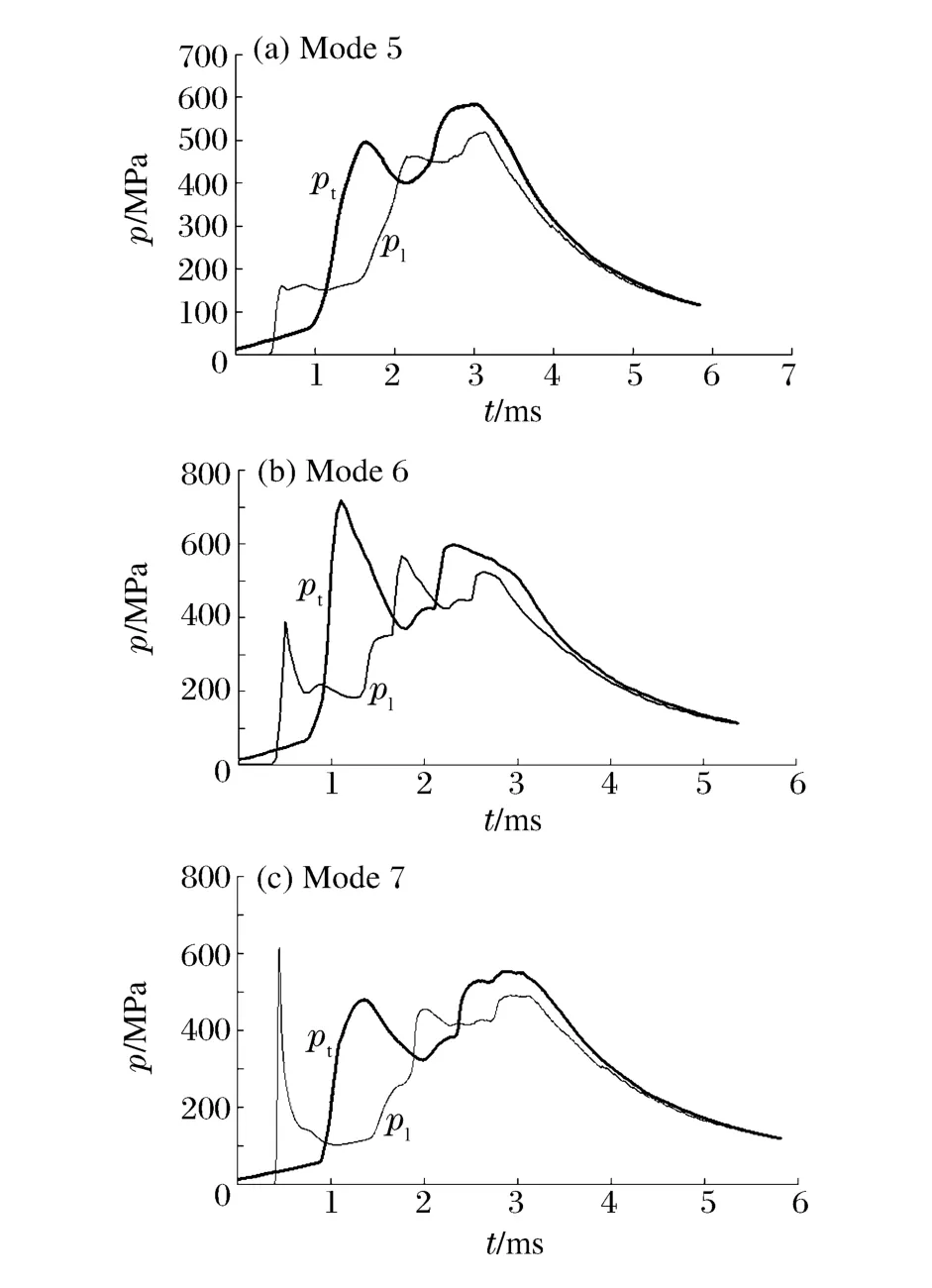
图4 破碎方式5~7 膛内压力时间历程计算结果Fig.4 Computational results of barrel pressure vs.time
由表1 和图3 可见,当其他条件和发射药破碎形式相同时,膛底最大压力和弹底最大压力均随着破碎程度的增大而增大。由表1 和图4 可见,在弹底发射药床破碎程度较大时,当该部位的药床被点燃后将直接导致坡膛部位压力在很短时间内急剧升高,导致膛底压力急剧升高,这种压力变化规律可导致膛内最大压力超过火炮容许压力而形成膛炸。如破碎方式6 的膛底最大压力达到了717.9 M Pa,破碎方式7 的弹底最大压力达到了766.1 M Pa。

图5 76 mm 火炮膛炸时实测压力[21]Fig.5 Pressure measured in a breechblow of 76 mm gun
值得一提的是,图4(b)、(c)所示膛压曲线的变化规律与文献[21]给出的76 mm 火炮膛炸时实测膛压曲线类似,见图5。
6 结 论
将DCD 格式引入内弹道两相流动力学数值模拟,建立了一种新的两相流内弹道计算方法,无须人为附加粘性和人工滤波。将与压力有关的项进行变形,无须对气相和固相采用不同的格式,提高了计算精度。对某榴弹的内弹道过程进行了计算,计算与实验结果吻合较好,表明了计算的正确性。把破碎发射药床作为混合装药结构,用DCD 格式实现了发射药床破碎程度对发射安全性影响的数值模拟,为研究发射装药发射安全性问题提供了一种计算方法。
[1] 芮筱亭,贠来峰,沙南生,等.发射药装药发射安全性评定技术的研究进展[J].兵工学报,2005,26(5):690-696.RUI Xiao-ting, YUN Lai-feng,S HA Nan-sheng, et al.Advance on launch safety for gun propellant charge[J].Acta Armamentarii,2005,26(5):690-696.
[2] 金志明,翁春生.高等内弹道学[M].北京:高等教育出版社,2003.
[3] 周彦煌,王升晨.实用两相流内弹道学[M].北京:国防工业出版社,1990.
[4] H arten A.A high resolution scheme for the com putation of weak solution of hyperbolic conservation law s[J].Journal of Com putational Physics, 1983,49:357-393.
[5] 水鸿寿.一维流体力学差分方法[M].北京:国防工业出版社,1998:364-370.
[6] 金志明,翁春生.火炮装药设计安全学[M].北京:国防工业出版社,2001.
[7] 郭永辉,田宙,郝保田.隐式TVD 格式在气液两相爆轰数值模拟中的应用[J].应用数学和力学,2000,21(6):654-660.GUO Yong-hui, TIAN Zhou, H AO Bao-tian.Implicit TVD schemes applied to gas-droplet detonation calculation[J].Applied Mathematics and Mechanics,2000,21(6):654-660.
[8] 洪滔,秦承森.爆轰波管中铝粉尘爆轰的数值模拟[J].爆炸与冲击,2004,24(3):193-200.H ONG Tao, QIN Cheng-sen.Numerical simulation of dust detonation of aluminum pow der in explosive tubes[J].Explosion and Shock Waves, 2004,24(3):193-200.
[9] JIANG Zong-lin, Takayama K, CHEN Yao-song.Dispersion conditions for non-oscillatory shock capturing schemes and its applications[J].Computational Fluid Dynamics Journal,1995,4(2):137-150.
[10] JIANG Zong-lin, H UANG Yong-hui, Takayama K.Shocked flow s induced by super sonic projectiles moving in tubes[J].Computers&Fluids,2004,33(7):953-966.
[11] 胡宗民,牟乾辉,张德良.爆轰波在弯管内传播过程数值分析[J].计算物理,2004,21(5):408-414.H U Zong-min, MU Qian-hui, ZHANG De-liang.Numerical simulation of gaseous detonation w ave propagation through bends with a detailed chemical reaction model[J].Chinses Journa of Computational Physics,2004,21(5):408-414.
[12] 胡宗民,高云亮,张德良,等.爆轰波在楔面上反射数值分析[J].力学学报,2004,36(4):385-392.H U Zong-min, GAO Yun-liang, ZH ANG De-liang.Numerical simulation of gaseous detonation reflection over w edges with a detailed chemical reaction model[J].Chinese Journal of Theoretical and Applied Mechanics,2004,36(4):385-392.
[13] 孙宇峰,张德良,胡宗民,等.氢氧爆轰波在变截面扩张管道中传播的数值模拟[J].爆炸与冲击,2004,24(5):385-390.S UN Yu-feng, ZHANG De-liang, HU Zong-min, et al.Numerical simulation of hydrogen2oxygen detonation w ave propagation in an expansion chamber[J].Explosion and Shock Waves,2004,24(5):385-390.
[14] 常利娜,姜宗林.球面聚心气相爆轰波传播过程的数值研究[J].力学学报,2006,38(3):296-301.CH ANG Li-na,JIANG Zong-lin.Numerical investigation on propagation of spherically imploding gas detonation[J].Chinese Journal of Theoretical and Applied Mechanics, 2006,38(3):296-301.
[15] JIANG Zong-lin.On dispersion-controlled principles for non-oscillatory shock-capturing schemes[J].Acta Mechanica Sinica,2004,20(1):1-15.
[16] S teger L, Warming R F.Flux vector splitting of the inviscid gas dynamic equations with application to finite difference methods[J].Journal of Computational Physics,1981,40:263-293.
[17] 芮筱亭,贠来峰,王浩,等.发射装药挤压破碎的试验模拟[J].兵工学报,2004,25(4):498-502.RUI Xiao-ting, YUN Lai-feng, WANG Hao, et al.A study on the experimental simulation for bursting of the charge bed[J].Acta Armamentarii,2004,24(4):498-502.
[18] 杨均匀,袁亚雄,张小兵.发射药破碎对火炮射击安全性影响的研究综述[J].弹道学报,1999,11(4):92-96.YANG Jun-yun, YUAN Ya-xiong,ZH ANG Xiao-bing.Research survey of the effect of grain fracture on the fire safety in solid propellant gun[J].Journal of Ballistics, 1999,11(4):92-96.
[19] 贠来峰,芮筱亭,王浩,等.对发射装药引起膛炸机理的讨论[J].兵工学报,2007,27(2):153-157.YUN Lai-feng, RUI Xiao-ting, WANG Hao, et al.Discussion about mechanism of breech-blow caused by gun propellant charge[J].Acta Armamentarii,2007,27(2):153-157.
[20] Zimmermann G,Cü tlin E.Experimental study of the response of gun propellant charges to shaped charge Jet impact loading[C]∥17th International Symposium on Ballistics-Midrand.South Af rica,1998.
[21] 袁亚雄.火炮膛内压力波研究综述[J].兵工学报武器分册,1990(2):47-56.
