基于定量结构-性质相关性的烃类物质爆炸下限预测*

潘 勇,蒋军成,王 睿

(1.中国科学技术大学火灾科学国家重点实验室,安徽 合肥230026;2.南京工业大学城市建设与安全工程学院,江苏 南京210009)

1 引 言

爆炸极限是评价可燃气体或蒸气爆炸危险性的重要参数之一,在防爆技术中应用广泛。它是风险评估以及确定可燃物质储存、运输、生产、使用安全性的依据之一;在监测监控技术中,它是一个重要的爆炸指示参量。因此,掌握各类可燃物质的爆炸极限数据具有重要的现实意义。

通过实验测定是目前获取爆炸极限数据的有效方法。但实验方法对设备要求高、工作量大;实验结果影响因素众多,差别较大。同时,对于测量上有困难或尚未合成的物质,也无法基于实验进行测定。因此,有必要开发简便可靠的爆炸极限理论预测模型,以弥补实验方法的不足。已有的爆炸极限理论预测方法主要包括经验关联法和基团贡献法2 大类[1],这些方法具有计算简单、使用简便等优点。然而,在实际使用过程中也存在明显的缺陷:经验关联法需要使用临界压力、等张比容等不常见的物化参数,而这些参数的实验数据往往本身就比较缺乏;基团贡献法的应用范围则受研究体系的影响较大,如果某个基团不在建模时选取的那组基团范围之内,那么对于含有该基团的化合物就无法应用该模型进行预测。因此,上述方法的应用范围都具有较大的局限性,限制了在实际工程中的进一步应用。

相关研究[2-3]表明,定量结构-性质相关性研究是一种能够根据分子结构实现有机物理化性质预测的有效方法,它根据化合物性能与分子结构密切相关的原理,寻求分子结构与物质性质之间的内在定量关系。其基本假设是有机物的性能与分子结构密切相关,分子结构不同,性能就不同。而分子结构可以用反映分子结构特征的各种参数来描述,即有机物的理化性质可用化学结构的函数来表示。根据对分子结构参数和实验数据的内在定量关系,采用合适的统计建模方法进行关联,建立分子结构参数与理化性质之间的关系模型。一旦建立了可靠的QSPR 模型,仅需分子的结构信息,就可预测新的或尚未合成的有机物的各种性质。目前,该方法已被广泛应用于有机物理化性质及生物活性的预测研究[3]。

本文中根据QSPR 研究基本原理,从分子结构角度出发,对354 种烃类物质的爆炸下限与其分子结构间的内在定量关系进行研究,建立根据分子结构预测烃类物质爆炸下限的理论模型。

2 研究方法

2.1 数据来源

实验数据的准确度直接影响到所建QSPR 模型的预测精度。爆炸下限实验值与其测定方法和测定装置有关,由于不同研究者采用的实验装置和方法不同,测定的爆炸下限数据之间存在一定的差异。为排除这些因素可能对预测结果带来的影响,确保实验样本的可靠性和标准化,本文中统一选用美国化学工程师协会下属DIPPR 数据库中的354 种烃类化合物的爆炸下限数据作为实验样本。这些化合物涵盖广泛的化学多样性空间,为建立有效的预测模型奠定了基础。

2.2 结构参数的计算和删减

要想寻求化合物性能与其分子结构间的相关性,必须首先对反映化合物分子结构特征和信息的各种结构参数(如拓扑参数、组成参数、电性参数以及几何参数等)进行计算,以获取分子的结构信息,实现分子结构的参数化描述。本文中首先将所有样本化合物结构输入Hyperchem 7.0 程序中,采用分子力学方法MM+进行初步优化,在此基础上用半经验方法AM1 进一步进行几何优化。随后将优化完的分子结构输入Dragon 2.1 程序中,对化合物的各种结构参数进行计算。通过计算,每个化合物均得到1 481 种结构参数。

同时,为避免建模过程中“机会相关”现象的发生,必须预先对众多的结构参数进行删减,以剔除那些不能为模型提供有用信息的参数。首先,对于那些对所有化合物来说数值为常数或者近似常数(变化较小)的结构参数,由于无法对导致性质差别的结构差异性进行有效表征,因此被删除;同时,对于两者之间相关系数大于0.96 的任意2 个结构参数,由于存在“共线性”,因此其中之一也被删除。经过删减,共剩下445 种结构参数进行下一步的特征变量筛选。

2.3 基于遗传算法的特征变量选择

如何从众多的结构参数中应用特征变量选择方法筛选出与目标性质最密切相关的结构参数,是QSPR 研究非常关键的问题。目前常用的特征变量选择方法主要包括3 类:(1)基于多元线性回归(M LR)的变量筛选方法,如向前/后选择变量法、逐步回归法等;(2)基于偏最小二乘(PLS)的变量筛选法,包括修正PLS 权重或系数以消除模型中无用变量的方法等;(3)基于搜索算法的变量筛选方法,如模拟退火法、遗传算法(GA)等搜索算法和M LR、PLS 等多种建模方法相结合的变量筛选方法。其中,第1 类方法适用于变量间不存在多重共线性数据的变量筛选,优点是方法简单直观,缺点是它们不能遍历所有的变量组合,也就不能保证寻找到变量空间里的最优解。第2 类方法与第1 类方法类似,仅搜索变量空间的某些范围,而不具备全局搜索能力,因此他们得到的常常是变量空间的局部最优解,而非全局最优解。

遗传算法是J.H.Holalnd[3]于1975 年最早提出的一种模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。它对需要解决问题的参量进行编码运算,并沿多种路线进行平行搜索,一般不会陷入局部最优的陷阱中,能够在多个局部较优中找到全局最优解。由于GA 具有相当强的搜索能力,当它与MLR、PLS 等建模方法相结合后,在一定条件下能够在有限的时间内搜寻到变量空间的最佳模型。因此,近年来GA 在QSPR 研究中得到了较为广泛的应用[5]。

本研究将GA 与PLS 相结合(GA-PLS),对剩余的445 种结构参数进行优化筛选,找出与爆炸下限最密切相关的结构参数作为分子描述符,表征化合物的结构特征。GA-PLS 程序通过Matlab 软件实现,选用“留1/10 法”交互验证的均方根误差(RMS)作为适应度函数。“留1/10 法”交互验证是指从训练集中每次筛除训练样本数的1/10 个化合物,用其余的化合物建模,来预测所筛除化合物的性质,这样得到一个交互验证的RMS 来评价模型性能的好坏。GA-PLS 所选用的其他相关参数为:种群规模30;初始染色体串长度5;最大染色体串长度30;突变概率1%;最大主成分数由对包含所有自变量的模型进行交互验证确定(≤15);最大进化代数100。

2.4 预测模型的建立

最优分子描述符确定以后,以它为输入变量,分别采用多元线性回归和支持向量机2 种方法,对烃类物质爆炸下限与分子描述符间的内在定量关系进行关联,建立相应的预测模型。

多元线性回归分析是一种较为常用的多元统计方法,它以线性最小二乘为基础,通过对输入变量和输出变量间的内在定量关系进行统计学习,建立相应的线性模型。本文中MLR 分析采用统计分析软件SPSS 11.0 实现,在95%置信区间,采用全回归算法对烃类物质爆炸下限数据与其分子描述符数据之间的线性关系进行拟合。

支持向量机(SVM)算法是V.N.Vapnik 等[6]在统计学习理论的基础上,于1995 年提出的一种新型机器学习方法。其基本思想是通过事先确定的非线性映射将输入向量x 映射到一个高维特征空间中,然后在此高维空间中构建最优超平面,将问题转化为2 次规划。在2 次规划中,目标函数只涉及内积运算。如果采用核函数就可以避免在高维空间进行复杂运算,而通过原空间的函数来实现内积运算。因此,选择适当的内积函数就可以实现某一非线性变换后的线性计算,而计算复杂度却没有增加。由于SVM 具有严格的理论基础,能较好地解决小样本、非线性、高维数和局部最小等实际问题,因此在QSPR 研究领域也开始得到应用[7]。本文中SVM 算法采用Libsvm 软件运行。为获得最佳的泛化能力,在建模过程中需要调节相应的参数组合,即选择合适的核函数、确定核函数的参数、惩罚系数C 以及ε-不敏感损失函数中ε的大小。目前实际应用中最多的是径向基(RBF)形式的核函数,它具有较高的学习效率和学习速率。对于RBF核函数,最重要的参数是核函数的宽度γ,它与C 及ε一起,决定了SVM 的泛化能力及预测性能。由于这几个参数之间有很大的相关性,因此采用格点搜索方法寻找最优的参数组合。采用“留一法”交互验证方式进行模拟,最优模型所对应的那组参数即被确定为最优参数。

2.5 模型验证

模型验证对于QSPR 研究至关重要,在QSPR 模型建立以后,必须对模型的稳定性、预测能力及泛化能力进行检验。常用的验证方法有内部验证与外部验证2 种。“留一法”交互验证是常用的内部验证方法,其结果以“留一法”交互验证的复相关系数表示。内部交互验证主要是为了检验模型的稳定性以及其内部预测能力,而相关研究表明[8],内部验证结果的好坏并不能说明其外部预测能力的大小,对模型预测能力的评价必须通过对未参与训练的物质进行预测,即外部验证的方式来进行。通过对预测集化合物进行外部验证,既能够体现模型对未参与训练的样本的真实预测能力,又能够反映模型的泛化能力。模型的外部预测能力常用交互验证的外部复相关系数进行衡量。因此,将样本集随机划分为训练集(样本总数80%)和预测集(样本总数20%)2 部分,其中,训练集主要用于变量筛选和构建预测模型,预测集则主要用于对所建模型进行外部验证。

此外,均方根误差RMS 和平均绝对误差AAE 作为重要的统计学参数,也被用来衡量所建模型的估计能力及预测性能。

3 结果与讨论

3.1 GA-PLS结果

运用GA-PLS 方法进行特征变量筛选,通过比较各模型预测RMS 的大小,确定本研究中与烃类物质爆炸下限最密切相关的4 个结构参数列于表1。表中,x1、x 2 和x3均属于拓扑描述符,主要描述分子中原子的连接信息。其中,x1与分子的相对顶点距离复杂度有关;x2则主要描述分子的形状,与分子中元素的差异度密切相关;x3则主要反映整个分子的拓扑结构。x4属于RDF 描述符,主要描述整个分子中的原子间距离信息,除此之外,它还与分子中键的距离、环的类型、平面和非平面体系及原子类型等信息有关。

表1 GA-PLS筛选出的结构参数Table 1 The descriptors selected by GA-PLS

从以上讨论可以看出,4 个结构参数主要与分子的一些简单结构特征有关,如分子的大小和形状、分子中原子的分布等。因此,可以将影响烃类物质爆炸下限的主要结构特征归纳为分子的大小、形状以及分子中原子的分布信息等。

对于任意已知分子结构的化合物,上述4 个结构参数均可以通过Dragon 软件进行计算,各参数的具体计算公式及过程可参见文献[9]。

3.2 MLR 模型结果

以GA-PLS 提取的4 个结构参数作为输入变量,针对训练集样本,运用M LR 方法建立爆炸下限线性预测模型

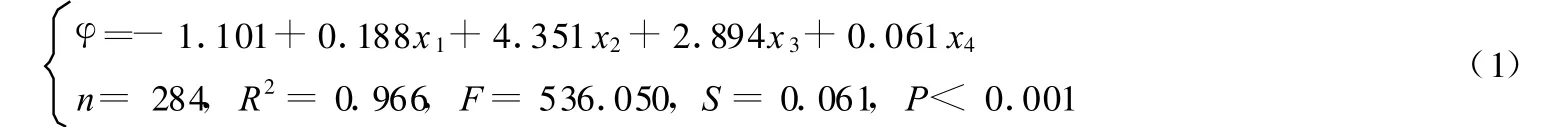
式中:φ为爆炸下限,n 为样本数,R2为复相关系数,F 为F 检验值,S 为标准误差,P 为方程的显著性概率。由式(1)可知,模型具有较高的相关系数和较低的标准误差,说明模型是可靠的;显著性概率远小于0.05,表明回归方程具有统计学意义。

随后,应用式(1)分别对训练集样本和预测集样本进行预测。对预测集中70 个样本的预测值见表2,对所有样本所得的爆炸下限预测值与目标值的比较见图1,模型的主要性能参数见表3。

表2 预测集样本爆炸下限预测值Table 2 The predicted values for the test set

表3 MLR 和SVM 模型的主要性能参数比较Table 3 Performance parameters obtained by SVM and MLR models

3.3 SVM 模型结果

为了与MLR 模型具有可比性,SVM 模拟中选取的训练集和预测集与M LR 相同,采用同样的4 个结构参数作为模型输入变量。通过格点搜索方法确定SVM 模型的最优参数如下:C=512,ε=0.031 25,γ=0.25,相应的支持向量数为129。应用所建模型分别对训练集样本和预测集样本进行预测。对预测集中70 个样本的预测值见表2,对所有样本所得的爆炸下限预测值与目标值的比较见图2,模型的主要性能参数见表3。

图1 MLR 模型爆炸下限预测值与目标值的比较Fig.1 Comparison between the predicted and observed LFL by MLR

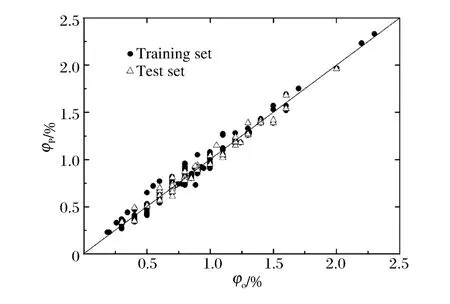
图2 SVM 模型爆炸下限预测值与目标值的比较Fig.2 Comparison betw een the predicted and observed LFL by SVM

3.4 模型稳定性分析

为进一步排除所建模型可能存在的“机会相关”现象,采用“y-scrambling”方法分别对MLR 和SVM 模型进行验证,评估2 个模型对“机会相关”现象的依赖程度。首先将训练集样本中的自变量x 保持不变,将对应的应变量y 顺序随机打乱,使应变量和自变量不再对应,以消除两者之间存在的内在定量关系;随后,针对上述改变序列的样本集建立新的QSPR 模型,并对其相关性能参数如RMS 等进行计算;将上述过程重复50 ～100 次,获得某一相对“最优”的预测模型,并将其与基于原始样本数据建立的实际预测模型进行比较。若实际模型的性能参数明显优于“最优”模型,则认为原始样本数据中存在真正的QSPR 关系,所建立的预测模型不存在“机会相关”现象。

将“y-scrambling”方法针对2 个预测模型分别运行100 次,对于MLR 模型,所得最小RMS 为5.95,对于SVM 模型,最小RMS 为4.71,两者均分别接近原始模型预测误差的100 倍。由此可见,只有在使用正确的应变量数据时才能产生合理的QSPR 模型,因而本文中所建立的预测模型不存在“机会相关”现象,具备较强的稳定性。

此外,还给出了2 种模型的预测残差分布图(图3、4)。从图中可以看出,2 种模型的预测残差都均匀且随机分布于0基准线的两侧,可见预测模型在建立过程中未产生系统误差。

图3 M LR 模型爆炸下限预测残差图Fig.3 Plot of the residuals versus the observed values for the M LR model

图4 SVM 模型爆炸下限预测残差图Fig.4 Plot of the residuals versus the observed values for the SVM model

3.5 模型的比较与分析

3.5.1 M LR 模型与SVM 模型的比较

从表3 可以看出,2 种预测模型的精度均令人满意,其中MLR 模型的预测平均绝对误差为0.041%,S VM 模型的预测平均绝对误差为0.036%,均在实验误差允许范围之内。这说明本文中基于遗传算法所筛选出的4 个结构参数能够有效地表征与烃类物质爆炸下限密切相关的结构特征,同时基于这些参数所建立的预测模型能够成功地对未知物质的爆炸下限进行预测。

此外,从表3 还可以看出,无论是对于训练集还是预测集,SVM 模型的性能都要明显优于MLR 模型。原因可能主要在于以下2 方面:一是烃类物质爆炸下限与其分子结构之间可能存在着较强的非线性关系,与线性MLR 方法相比,S VM 方法因具有强大的非线性拟合能力而体现出较强的优越性;同时,SVM 是一种基于结构风险最小化的机器学习方法,它追求置信范围值的最小化,而非训练误差的最小化,因此与MLR 相比具有更好的泛化性能。但是,SVM 方法建立的是一种“黑箱”模型,不能给出直观的数学模型,因而无法准确了解各分子描述符对模型的贡献值,而这些正是MLR模型的优势。因此,这2 种方法各有利弊,并存在一定的互补性。

3.5.2 与其他预测模型的比较

为进一步验证本文预测模型的优越性,将其与T.A.Albahri[10]所建立的烃类物质爆炸下限预测模型进行比较。关于样本集的大小,Albahri 模型的样本数(472)大于本文模型(354),然而,Albah ri 模型的外部预测样本数(18)却明显少于本文模型(70),仅占其样本总数的4%左右,不满足QSPR 研究的一般要求[8];关于模型的输入参数,Albahri 模型基于基团贡献法原理以19 个分子基团作为输入参数,而本文仅以4 个结构参数作为分子描述符,一方面使所建立的预测模型更为简便和稳固,另一方面因结构参数具有明确的物理意义因而便于对影响爆炸下限的重要结构特征进行解释和研究;关于模型性能参数,T.A.Albahri 建立的非线性预测模型(0.04%)与本文MLR 模型相比(0.045%)较优,与SVM 模型(0.035%)相比则较差,这验证了前文关于爆炸下限与分子结构之间可能存在较强非线性关系的推断;关于模型的适用范围,Albahri 模型基于基团贡献法原理建立,其应用范围受研究体系的影响较大,如果某个基团不在建模所选取的那组基团范围之内,那么对于含有该基团的化合物就无法应用该模型进行预测,而本文预测模型则以仅需分子结构就能计算的分子结构参数作为描述符,理论上能够对所有已知分子结构的烃类物质进行预测,适用范围更广。由此可见,与已有的烃类物质爆炸下限预测模型相比,本文模型在模型稳定性、模型解释、模型预测能力和适用范围等方面都具有一定的优越性。

4 结 论

应用遗传算法从大量分子结构参数中优化筛选出与烃类物质爆炸下限最密切相关的一组结构参数,得出了影响爆炸下限的主要结构特征为分子的大小、形状以及分子中原子的分布信息。同时,以上述结构参数作为分子描述符,分别应用MLR 和SVM 方法建立了相应的爆炸下限预测模型,实现了根据分子结构预测爆炸下限的功能。

[1] Vidal M, Rogers W J, Holste J C,et al.A review of estimation methods for f lash points and f lammability limits[J].Process Safety Progress,2004,23(1):47-55.

[2] Katritzky A R, Lobanov V S, Karelson M.QSPR:The correlation and quantitative prediction of chemical and physical properties from structure[J].Chemical Society Review s,1995,24(4):279-287.

[3] 王连生,韩朔睽.分子结构、性质与活性[M].北京:化学工业出版社,1997.

[4] H olland J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan Press,1975.

[5] Niculescu S P.Artificial neural netw orks and genetic algorithms in QSAR[J].Journal of Molecular Structure:TH EOCH EM,2003,622(l-2):71-83.

[6] Vapnik V N.The nature of statistical learning theory[M].New York:Springer,1995.

[7] 刘焕香.基于支持向量机方法的QSAR/QSPR 在化学、生物及环境科学中的应用研究[D].兰州:兰州大学,2005.

[8] T ropsha A,Gramatica P, Gombar V K.The importance of being earnest:Validation is the absolute essential for successful application and interpretation of QSPR models[J].QS AR&Combinatorial Science,2003,22(1):69-77.

[9] Todeschini R,Consonni V.Handbook of molecular descriptors[M].Weinheim:Wiley-VCH, 2000.

[10] Albahri T A.Flammability characteristics of pure hydrocarbons[J].Chemical Engineering Science,2003,58(16):3629-3641.