爆炸膨胀环实验数据处理方法讨论＊

汤铁钢，桂毓林，李庆忠，陈永涛，童慧峰，刘仓理

（中国工程物理研究院流体物理研究所冲击波物理与爆轰波物理国防科技重点实验室，四川 绵阳621900）

1 引 言

爆炸膨胀环实验是在1维应力状态假定下研究材料高应变率拉伸加载时的动态性能，包括本构关系和断裂特性，长期以来，爆炸膨胀环实验数据的处理一直困扰着研究者们。P.C.Johnson 等［1］、C.R.Hoggatt等［2］运用爆炸膨胀环实验技术测试了许多工程材料的本构关系数据，当时只能测量膨胀环的位移历史，数据处理时需要对膨胀环的位移历史进行2次微分，数据精度一直困扰着实验数据的可用性。直到R.H.Warnes等［3］利用激光速度干涉仪（VISAR）直接测量了爆炸膨胀环的径向膨胀速度，克服了求流动应力时位移关于时间2次微分的困难。在数据处理时，R.H.Warnes等对速度历史曲线采用2次关系式进行了拟合，然后进行微分计算加速度。R.H.Warnes等同时指出，采用更高阶的关系式进行拟合，可以对速度进行更好地近似拟合，但是求解出的应力应变关系却令人费解；他们还指出，其他的一些光滑数据的方法也没有得到实验检验。F.Llorca等［4］通过数值模拟对膨胀环实验中速度历史的处理进行了分析，尝试直接对测试获得的离散速度数据进行处理，结果获得的流动应力应变关系曲线振荡非常剧烈，而采用线性和2项关系式拟合后，得到的流动应力应变关系与SCG 模型结果比较接近。

本文中，尝试采用不同的数据处理方法对爆炸膨胀环实验获得的速度曲线进行处理，讨论数据窗口选取对处理结果的影响，同时对数据处理方法中存在的一些问题进行分析。

2 膨胀环运动分析

对于自由飞行阶段的膨胀环，膨胀环中的径向应力很小，近似看作零，因此膨胀环仅在环向应力作用下作减速运动，如图1所示，取其中一环向单元建立运动方程

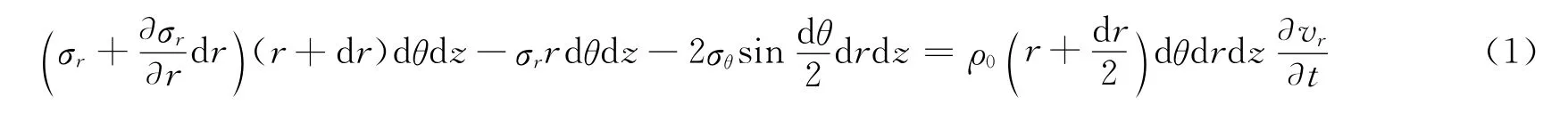
金属环在自由膨胀期间径向应力为零，得到周向应力的运动方程

式中：r0为膨胀环初始半径。将式（4）对时间t求导数，得

图1 膨胀环运动分析示意图Fig.1 Movement analysis of an expanding ring

3 膨胀环速度曲线

3.1 速度历史特征及数据窗口的选取

在爆炸膨胀环实验中，采用激光干涉技术可以获得膨胀环的径向速度历史，以1 发无氧铜膨胀环实验结果为例进行说明，速度历史如图2所示。从速度历史可以看出，膨胀环具有较长一段自由膨胀过程，即速度历史上的B 段，通常称之为有用数据窗口，A 段为冲击加载及应力波在膨胀环壁内的反射阶段，C 段为膨胀环发生了失稳或者断裂阶段，对于处理膨胀环材料的应力－应变－应变率关系，A 段和C 段均为无用数据。为了揭示数据处理方法对结果的影响，本文中选取的这条速度曲线的B 段的斜率不单调变化。

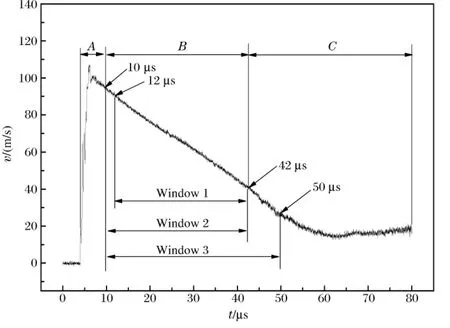
图2 膨胀环速度历史及数据窗口选取Fig.2 Radial velocoty－time history of the expanding ring and the selection of data windows

如何合理地选取数据窗口B 段，是数据处理的前提。对于此发实验，通过回收样品测量确定膨胀环的断裂应变约0.14，对应的断裂时间约50μs，显然，数据窗口的选取只能在50μs之前。从速度历史上看（见图2），在42～50μs之间速度有些振荡，数据是否可用需要讨论。为了更好地检验数据处理方法，拟在速度曲线上选取大部分区域重合的3个数据窗口，分别记为窗口1、窗口2、窗口3，如图2所示。窗口1对应时间12～42μs，认为是最理想的数据窗口，窗口2对应时间10～42μs，窗口3对应时间10～50μs。从速度曲线看，窗口2相对窗口1没有明显的趋势变化，而窗口3中的后8μs速度趋势有明显变化。

3.2 数据拟合

在速度曲线上对选取的窗口数据截取后进行数据拟合，分别进行线性关系式、2次关系式、3次关系式拟合，拟合后进行微分求解加速度。线性关系式、2次关系式、3次关系式的表达式分别为

对于窗口1～3中的数据采用以上3种关系式进行拟合，求解应力时，首先要对拟合的速度公式进行求导得到加速度，所有关系式中的常数项a 求导后消失。线性拟合时，加速度（即速度斜率）为常数b，2次关系式拟合时，加速度为时间的线性函数，3次关系式拟合时，加速度为时间的2次函数。

4 数据处理结果分析

4.1 拟合方法对数据处理结果的影响

采用3种拟合关系式对实验数据进行处理，首先对图2 中窗口1（12～42 μs）数据进行处理，获得的应力应变关系见图3。线性拟合关系式获得的应力应变关系也基本上呈线性关系，2 次关系式拟合时获得的应力应变关系与线性拟合在所选的数据窗口中较接近，而采用3次关系式拟合时，应力应变关系呈现为上凹的曲线。

4.2 数据窗口选取对结果的影响

对于测试获得的含有一定噪声且离散的速度数据，很难准确界定有效数据窗口的边界，因此，数据窗口的选取存在一定的人为性。通过改变数据窗口的宽度，来讨论数据窗口对应力应变关系的影响。

首先采用线性关系式和2次关系式拟合对3个窗口数据进行处理，获得的应力应变关系如图4所示。采用线性拟合时，窗口宽度的改变直接影响速度的斜率（常数），即直接影响应力的幅值，因此获得应力应变关系为3条相互平行的直线（实际上是与位移线性相关的曲线），其中窗口1和窗口2的结果比较接近，而窗口3的结果偏离稍大。采用2次关系式拟合时，窗口1、窗口2数据处理获得的应力应变关系表现为略有下凹的曲线，而窗口3数据处理获得的应力应变关系却为明显的上凹曲线，尤其是后半段与前2个数据窗口结果偏离较大，这与原始速度数据的后期振荡是相关的。

采用3次关系式拟合对3个窗口数据进行处理，获得的应力应变关系如图5所示。对于3个不同的数据窗口，采用3次关系式拟合处理结果均为明显的上凹曲线，数据窗口的选取对于3次关系式拟合处理结果的影响不及低阶关系式明显，但是处理出的应力应变关系却不同于一般的拉伸应力应变关系曲线特征。

图3 窗口1数据3种拟合方法处理结果Fig.3 Processing results of data window 1by three fitting expressions

图4 3个数据窗口线性拟合及2次关系式拟合处理结果Fig.4 Processing results of three different data windows

4.3 分析讨论

从应力计算表达式看，采用线性拟合时，加速度为常数，应力与位移（或应变）成线性增长关系，反映了材料的应变硬化效应。实际上，由公式（5）可知，随着位移的增加，膨胀环的拉伸应变率下降。如果考虑材料的应变率效应，材料中的应力也应该随着应变率的降低而降低，线性拟合不能反映材料的应变率效应。因此，对于应变率敏感的材料，线性拟合是不合适的。

以上研究发现，对于膨胀环速度曲线上人为选取的任何窗口数据，3次关系式拟合都是上凹曲线，说明高阶关系式虽然能较好拟合膨胀环的速度历史。但由此处理得到的应力应变关系却与物理规律似乎背离，本文中推测R.H.Warnes等［3］在数据处理时可能也出现类似问题，即他所说的令人费解的原因。这到底是原始速度数据的问题，还是数据处理方法的问题，需要更进一步的分析。

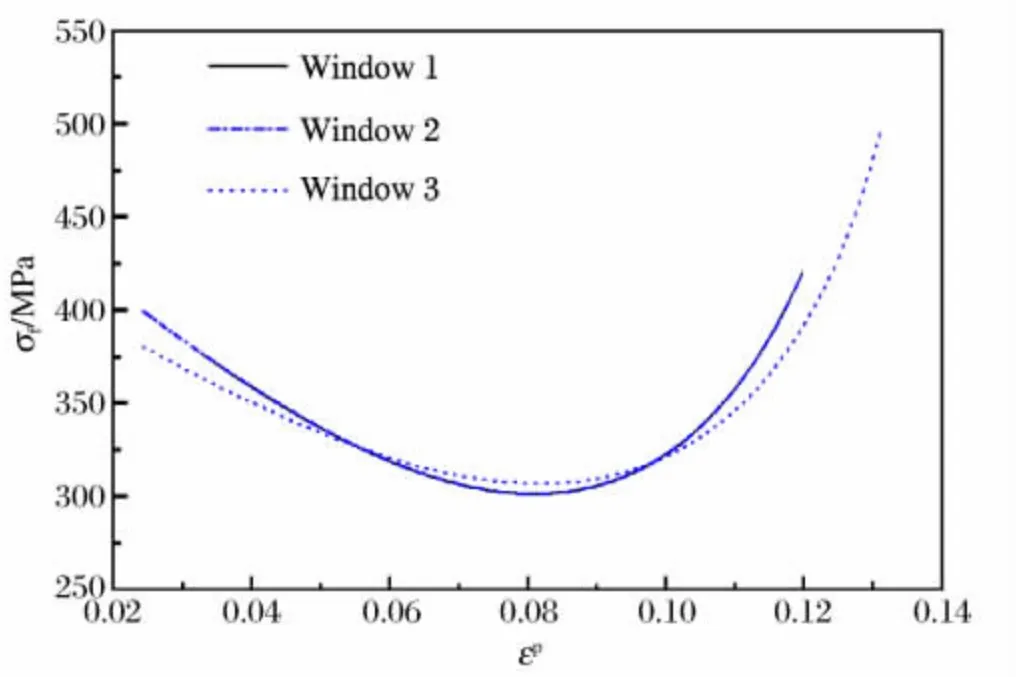
图5 3个数据窗口3次关系式拟合处理结果Fig.5 Processing results of three different data windows by trinomial fitting

图6 5种不同拟合关系式对窗口1数据的处理结果Fig.6 Processing results of data window 1by five different fitting expressions

在不能明显判断数据是否可用的条件下，随着窗口数据的增加（即增加窗口的时间长度），2次关系式拟合处理结果也出现了明显的偏离，如图4中的窗口3数据结果。到底是数据处理方法的问题还是数据窗口选取的问题呢？本文中尝试了另几种多次关系式，如

以及他们的组合关系式，对速度窗口中的数据进行拟合处理。结果发现，在窗口1中，多种关系式拟合结果基本一致，见图6，当最高次不大于2时，得到的结果偏差相对较小，而最高次项大于2时，获得应力应变关系为上凹曲线，从形式上可能偏离了物理规律。而对窗口2和窗口3中数据进行非线性拟合处理得到的应力应变关系均出现不同程度的发散，由此看来，数据窗口的准确选取是采用拟合方法进行膨胀环实验数据处理的基础。

5 数据光滑与差分方法

在膨胀环实验数据处理时为什么总是先对速度历史进行拟合呢？主要原因是测试的速度历史是离散的数据，而且测试的速度数据包含了噪声，速度曲线本身不光滑，直接差分求解加速度会带来极大的偏差。实际上，目前对于数据的光滑技术已经很成熟了，可以先对速度数据进行光滑，然后直接进行差分求解加速度。理论上讲，直接进行求解，能更好地反映每个时刻速度与应力的对应关系。另一个好处是，直接差分计算对窗口选取的依赖性较弱，因为差分方法可以计算出瞬时加速度，只依赖于瞬时的速度数据，不再需要拟合关系式。但由于膨胀环实验是在1维应力假定条件下进行的，数据处理时仍热需要确定合理的数据窗口，以确保所选取的膨胀环拉伸过程满足1维应力状态。

为了更好地澄清3次拟合关系式处理结果形式上异常的原因，采用Mathcad中的样条函数对速度曲线进行高阶光滑，然后进行直接差分计算，处理得到的应力应变关系与拟合关系式处理结果同列于图7中。令人惊奇的是，在窗口1中，3次关系式拟合处理结果与直接差分计算结果吻合很好。

由此看来，采用高阶关系式拟合进行处理时，出现结果异常的原因并非数据处理方法的问题，主要原因是来自原始数据的测试精度。采用VISAR 进行速度测试时，是典型的点测试，对于环向尺寸较大的膨胀环，VISAR 探头对准的任意一点，有可能是颈缩、断裂等现象发生的点，获得的速度历史就不能反映膨胀环的均匀膨胀过程。因此，在膨胀环实验中，速度测试最好是多点，采用平均速度进行数据处理会提高数据精度，单点速度测试会给数据处理结果带来很大的不确定性。

图7 直接差分方法与拟合方法处理结果的比较Fig.7Comparison of results by the fitting methods and the direct difference method

6 结 论

（1）对于爆炸膨胀环实验，速度数据窗口的合理选取是进行数据处理的前提，数据窗口的选取既要避开前期由于加载引起的速度振荡，也要避开后期由于膨胀环发生颈缩、断裂引起的速度振荡；

（2）速度曲线在数据窗口内斜率单调变化时，可以采用低阶关系式拟合进行处理，拟合关系式不超过2阶时，处理结果会比较接近；

（3）采用数据光滑技术和差分方法相结合的数据处理方法，能较好地反映速度历史和瞬时应力的对应关系，但同时要求速度测试具有较高的精度；同时澄清了在数据处理时采用高阶关系式拟合出现异常现象的原因是速度点测试方法带来的。

［1］ Johnson P C，Stein B A，Davis R S.Measurement of dynamic plastic flow properties under uniform stress［C］∥Symposium on the Dynamic Behavior of Materials.1963：195－198.

［2］ Hoggatt C R，Recht R F.Stress－strain data obtained at high rates using an expanding ring［J］.Experimental Mechanics，1969，9（10）：441－448.

［3］ Warnes R H，Duffey T A，Karpp R R，et.al.An improved technique for determining dynamic material properties using the expanding ring［C］∥Meyers M A，Murr L E.Shock Waves and High－strain－rate Phenomena in Metals.New York：Plenum Press，1981：23－36.

［4］ Llorca F，Juanicotena A.Expanding ring test：Numerical simulation－application to the analysis of experimental data［J］.Journal De Physique IV，1997，7：325－340.