猪后腿肌肉的动态拉伸性能*
2010-02-26王宝珍郑宇轩胡时胜
王宝珍,郑宇轩,胡时胜
(中国科学技术大学中国科学院材料力学行为和设计重点实验室,安徽 合肥230026)
1 引 言
近年来,交通事故、航天事故等对人身安全造成了非常大的危害,设计有效的防护装置保障人身安全成了当今世界的焦点问题,而这要求首先了解人体组织在冲击载荷下的力学性能。肌肉是人体组织的重要组成部分,质地柔软,其力学性能测试比硬组织的困难得多,因而相关研究较少。由于对人体组织进行冲击损伤试验不现实,通常用动物组织来近似替代。王宝珍等[1]对猪后腿肌肉材料的冲击压缩力学性能进行了研究,发现肌肉材料具有应变率敏感性和加载方向敏感性,且沿纤维方向的抗压强度比垂直纤维方向的低。由于肌肉材料的各向异性,抗拉、压性能差别大,冲击拉伸性能作为力学指标也应受到重视,但以往的研究多关注纤维方向的静态拉伸性能[2],动态拉伸力学性能还未见报道。
分离式Hopkinson 压杆(SHPB)[3]被广泛用于材料的动态压缩力学性能测试,研究者们还在此基础上发展了动态拉伸[4-6]、扭转[7]等试验技术。生物软组织动态力学性能试验中存在透射信号弱、应力均匀难以达到等问题,而且试样的夹持也存在很大的困难,再加上拉杆装置本身较复杂,目前仅见一篇关于颈椎骨韧带的动态拉伸性能研究[8]的报道,为方便试样的夹持采用了骨-韧带-骨试样,为测得微弱的透射信号,采用低阻抗的镁材料作为透射杆并结合高灵敏度的半导体应变片技术。然而对于超软的肌肉材料,透射信号更微弱,夹持更困难。本文中采用套管式霍普金森拉杆装置,设计适用于较软材料的拉伸夹具,用更低阻抗的尼龙杆作为透射杆,编写程序对粘弹性杆中波传播的弥散和衰减效应进行修正,拟得到猪后腿肌肉材料沿纤维方向和垂直纤维方向的动态拉伸应力应变曲线。
2 肌肉拉伸力学性能试验
2.1 试样准备
试样取自出生约150d的生猪。将该猪宰后约2h切下后腿肌肉,用切肉机沿纤维方向和垂直纤维方向切成3mm 厚的薄片,再用手术刀切成宽约12mm 的长条形试样。准静态试验试件有效长度为20.0mm,动态拉伸试验试件有效长度为2.5mm。每种应变率有效试样数为7个。试验过程中,待用试样浸泡在配置好的kreb溶液[9]中。
2.2 准静态拉伸试验
准静态试验在生物材料试验机上进行,装置如图1所示,并给出了夹具的实物图。通过旋转手柄,推动与螺丝固结的金属片,压紧软组织材料,为了减少试样滑脱现象,在与试样接触的两金属面粘上一定厚度橡胶片。利用该装置,对肌肉进行了沿纤维方向和垂直纤维方向的2种低应变率(0.02、0.1s-1)试验。同时,为研究肌肉试样在以上保存条件下,死后时间对其力学性能的影响,还对猪后腿肌肉试样在应变率为0.02s-1的拉伸速率下,间隔一定时间进行了测试。
2.3 套管式高聚物霍普金森拉杆装置
套管式霍普金森拉杆装置如图2所示,通过夹具将试样固定在入射杆和透射杆之间,在套管尾部,联接块和螺栓将其与里面的拉杆相连,实验时,子弹打击撞击块,套管产生一压缩波,到达螺栓处,转换为管内入射杆中的拉伸波,从而直接对试件实施冲击拉伸。

图1 生物材料试验机装置图Fig.1 Abiomechanical testing system

图2 套筒式Hopkinson拉杆装置Fig.2 A Hopkinson tensile bar in tubes
如果不考虑入射脉冲的产生方式,霍普金森拉杆的试验原理和霍普金森压杆的试验原理是一样的,都是建立在2个基本假定基础上的,即1维假定和均匀性假定。利用粘贴在杆上的应变片记录的脉冲信号,根据1维应力波理论和均匀性假定,可计算出试样的应变率、应变和应力为[5]


式中:E、A 和c0分别为杆的弹性模量、截面积和弹性波速;ls和As分别为试样的长度和截面积;εr和εt分别为反射应变和透射应变。
为了满足1维应力波理论,通常选用长径比较大的细长杆作为入射杆和透射杆。在软组织拉伸试验中,也会遇到透射信号太弱、应力均匀性很难达到等问题。在冲击压缩试验中,采用石英压电片作为传感器来检测微弱的透射信号以及检测应力均匀性的情况。而在拉伸装置中,石英片的使用比较困难。为了提高透射信号,选用低阻抗的尼龙杆作为透射杆,尼龙杆的波阻抗只有铝杆的10%左右,同时采用高灵敏度的半导体应变片来检测透射信号。但是使用高聚物杆有1个很大的困难就是由于其粘弹性特征,波形会发生弥散和衰减[10-12],需要对检测波形进行修正。而对于试样的应力均匀性问题,拉伸应力均匀过程与压缩类似。因此本文中也通过波形整形器和短试样的方法,提高入射波的升时,减少波在试样中传播1次的时间,从而使试样更早进入应力均匀性状态[13]。这里采用的有效拉伸长度与压缩试样厚度相同,也为2.5mm。
对于拉伸试验,还将面临的难题是试样的夹持,对普通的工程材料,可通过强力胶将试样固定在夹具上,然而肌肉材料不适用。为了保证试样不滑脱,且不改变其性能,设计了适合软组织材料使用的夹具,如图2所示。其夹持原理与准静态的夹具类似,旋转螺钉,通过金属压片和橡胶垫层压紧试样,夹具与杆之间通过螺纹连接。
采用以上拉杆装置对猪后腿肌肉进行动态拉伸试验,得到的典型波形如图3所示。

图3 猪后腿肌肉的典型试验波形Fig.3 Typical experimental waves for the porcine ham muscle
2.4 粘弹性波的弥散衰减修正
C.Bacon[10]对粘弹性杆的波形弥散和衰减进行了分析并提出了1种简单的测定粘弹性杆的传播系数γ(ω)的试验方法。1维细长圆柱形粘弹性杆受轴向冲击时控制方程为

传播系数γ(ω)反映材料本构引起的波的弥散和衰减的性质,可用粘弹性杆的衰减系数α(ω)和相速度c(ω)来表示

式(4)的通解为

式中:P(ω)、N(ω)为x =0处分别沿x 轴正向和负向传播的应力波引起的轴向应变的傅立叶变化,得

只需要在波导杆中粘贴应变片测得不相叠加的入射波εi和反射波εr,根据自由端面应力为0的条件,对波形进行傅立叶变换,便可得到传播系数的计算公式如下

式中:d 为应变片到杆自由面的距离。负号表示反射波和入射波方向相反,将负号应用到反射波形中,由此可确定粘弹性杆的衰减系数和相速度为
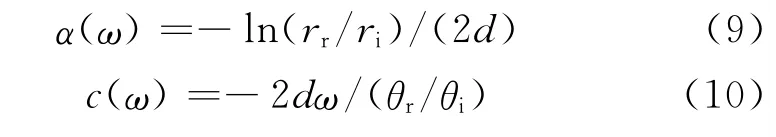
将得到的衰减系数和相速度代入式(7),然后进行逆傅立叶变换,可以修正肌肉试验实测的透射信号,从而得到试样端面实际受到的力。
采用以上介绍的波传播系数法,用Visual C++编制程序可得到传播系数并进行弥散和衰减的修正。图4给出了试验所用尼龙杆的衰减系数和相速度随频率变化的曲线。
2.5 夹具对波传播的影响
为了考察夹具对波形的影响,采用LS-DYNA 程序进行数值模拟,分别考察夹具对入射杆和透射杆波形的影响。这里使用2维轴对称模型,将平叉口部分等效为等截面积的圆柱体。入射杆和夹具为铝材,线弹性材料参数为:ρ=2.7t/m3,E=68GPa,ν=0.33。透射杆为尼龙杆,为了简化,这里也采用线弹性材料模型:ρ =1.17t/m3,E=4.9GPa,ν=0.33。考察入射杆时,在入射杆撞击端加载速度载荷,对比入射波和反射波的幅值,如图5(a)所示。考察透射杆时,在夹具前端加载速度载荷,对比加载波形与杆中波形,如图5(b)所示。发现夹具对波传播的影响可以忽略。

图4 尼龙杆的衰减系数和相速度Fig.4 Attenuation factors and phase velocities of nylon bars

图5 夹具对杆中波形的影响Fig.5 Wave propagation in the bars with clamps
3 试验结果及讨论
通过以上试验方法,得到了肌肉材料在不同应变率˙ε下,沿纤维方向和垂直于纤维方向的应力应变曲线,并根据统计学方差分析法,给出了标准误差线,如图6所示。
从图6可以看出,在准静态条件下,应力应变曲线具有相似的形状。开始阶段,应力应变曲线是非线性的,应力水平非常低,许多软组织都是如此,是组织的正常生理负荷区,称为“足趾”区[14],肌肉组织中含有多种蛋白分子,如肌动蛋白、肌球蛋白、肌联蛋白、胶原蛋白等,这些蛋白分子链结构中都包含螺旋结构,“足趾”区实际上是这些螺旋结构逐渐被拉直的过程。螺旋结构拉直后开始逐渐地弹性伸长,如果卸去载荷,则会回复原来的结构。应变继续增大,应力应变又进入非线性区,到达最大的应力值后,肌肉组织仍能承受一定的载荷,说明破坏是逐渐发生而不是突然发生的,图中准静态应力应变曲线给出了直到发生破坏时的情况。在高应变率时,螺旋结构还来不及伸直,因而几乎看不到“足趾”区。由于动态试样的破坏并非是首次加载时发生的破坏,因而本文的应力应变曲线未包含破坏时的应力和应变。
表1将猪后腿肌肉在2个加载方向上在2种低应变率下的极限强度σy和破坏应变εd用平均值±标准方差表示出来。采用SPSS软件进行1维方差分析,结果发现,在0.02、0.1s-1的应变率下,无论是沿纤维方向还是垂直于纤维方向拉伸,极限强度都显著不同,应变率增加,极限强度增加;同一应变率下,2个加载方向的极限强度也显著不同,沿纤维方向极限强度更大。然而,沿纤维方向上加载,2种应变率下破坏应变无显著不同,而垂直于纤维方向上,破坏应变显著不同。在同一应变率下,沿纤维方向和垂直于纤维方向,破坏应变无显著不同。

表1 猪后腿肌肉拉伸材料性能参数(N=7)Table 1 Tensile material properties for the porcine ham muscle(N=7)

图6 猪后腿肌肉在不同应变率下沿不同方向的应力应变曲线Fig.6Stress-strain curves of the porcine ham muscle at different stain rates along different directions
将应变为0.3、应变率分别为0.02、2 100s-1时的应力进行比较,发现在2个加载方向上应力都显著不同,沿纤维方向应力从(11.64±5.68)kPa到(146.06±36.08)kPa,沿垂直于纤维方向应力从(5.65±1.41)kPa到(137.88±2.62)kPa,动态时该应变下的平均应力比准静态时该应变下的平均应力有大幅的提高,表现出明显的应变率效应。在动态条件下,应变较小时,如应变为0.01,垂直于纤维方向的应力(29.92±5.68)kPa与沿纤维方向的应力(11.19±2.76)kPa显著不同,也即垂直方向的初始模量高于纤维方向的。但是当变形逐渐增加后,2方向的强度则无显著不同,纤维方向流动应力有逐渐高于垂直纤维方向的趋势。肌肉的力学性能与它的组织结构关系很大,当受拉伸时,在纤维方向,主要依靠紧密排列的肌纤维共同承担拉力的作用,纤维间的组织起支持作用,协调相邻纤维的变形。而在垂直纤维方向,则主要是依靠肌纤维间的结缔组织来承受拉力,肌纤维起传递拉力的作用,这造成2方向上拉伸性能的不同。

图7 死后时间对猪后腿肌肉力学性能的影响Fig.7 Effects of time after death on the dynamical properties of the porcine ham muscle
为考察在文中所用的保存试样方法下,死后时间对肌肉材料力学性能的影响,给出了应变为0.3时不同死后时间对应的应力,如图7所示。结果发现,在该保存条件下,生猪死后17h内,肌肉的力学性能无显著不同。也就是说,如果合理的保存试样,在有限的时间内,试验可以不考虑死后时间的影响,来考察加载方向和应变率的影响。文中得到的试验结果可为发展肌肉的本构模型提供依据。
4 结 论
采用套管式霍普金森拉杆装置对猪后腿肌肉的动态力学性能进行了研究。设计了肌肉拉伸所需的夹具,通过数值计算发现夹具对试验波形影响很小,可以忽略。
为了获得高信躁比的透射信号,采用了低阻抗的尼龙杆作为透射杆,自编程序对粘弹性中波的弥散和衰减进行了修正。结果发现猪后腿肌肉无论是沿纤维方向还是垂直纤维方向拉伸强度都具有应变率敏感性。准静态试验数据给出了直到组织发生破坏时的结果,沿纤维方向的破坏强度比沿垂直纤维方向的大,但破坏应变无显著差别。准静态的拉伸应力应变曲线具有典型的软组织材料拉伸变形特征,开始阶段为应力水平很低的“足趾”区。但在动态条件下,“足趾”区消失,这是因为组织中的螺旋状分子结构来不及伸直。特别是在垂直纤维方向,动态曲线开始阶段模量较大。不同加载方向力学性能的不同与肌肉组织的结构有关,沿着纤维方向主要依靠肌纤维承受拉力,而垂直纤维方向则主要依靠纤维间组织来承拉。
[1] 王宝珍,胡时胜.猪后腿肌肉的冲击压缩特性实验[J].爆炸与冲击,2010,30(1):33-38.WANG Bao-zhen,HU Shi-sheng.Dynamic compression experiments of porcine ham muscle[J].Explosion and Shock Waves,2010,30(1):33-38.
[2] Hawkins D,Bey M.A comprehensive approach for studying muscle-tendon mechanics[J].Journal of Biomechanical Engineering,1994,116(1):51-55.
[3] Kolsky H.An investigation of the mechanical properties of materials at very high rates of loading[J].Proceedings of the Physical Society:B,1949,62(11):676-700.
[4] Harding J,Wood E O,Campbell J D.Tensile testing of materials at impact rates of strain[J].Journal of Mechanical Engineering Science,1960,2(2):88-96.
[5] Nicholas T.Tensile testing of materials at high rates of strain[J].Experimental Mechanics,1981,21(5):177-185.
[6] Staab G H,Gilat A.A direct-tension split Hopkinson bar for high strain-rate testing[J].Experimental Mechanics,1991,31(3):232-235.
[7] Lewis L,Campbell J D.The development and use of a torsional Hopkinson-bar apparatus[J].Experimental Mechanics,1972,12(11):520-527.
[8] Shim V P W,Liu J F,Lee V S.A technique for dynamic tensile testing of human cervical spine ligaments[J].Experimental Mechanics,2006,46(1):77-89.
[9] SONG Bo,CHEN Wei-nong,GE Yun,et al.Dynamic and quasi-static compressive response of porcine muscle[J].Journal of Biomechanics,2007,40(13):2999-3005.
[10] Bacon C.An experimental method for considering dispersion and attenuation in a viscoelastic Hopkinson bar[J].Experimental Mechanics,1998,38(4):242-249.
[11] Salisbury C.Spectral analysis of wave propagation through a polymeric Hopkinson bar[D].Canada:University of Waterloo Press,2001:12-23.
[12] 刘孝敏,胡时胜,陈智.粘弹性Hopkinson 压杆中波的衰减和弥散[J].固体力学学报,2003,23(1):81-86.LIU Xiao-min,HU Shi-sheng,CHEN Zhi.The wave propagation attenuation and dispersion in a viscoelastic Hopkinsin pressure bar[J].Acta Mechanica Solida Sinica,2003,23(1):81-86.
[13] ZHU Jue,HU Shi-sheng,WANG Li-li.An analysis of stress uniformity for viscoelastic materials during SHPB tests[J].Latin American Journal of Solids and Structures,2006,3(2):125-148.
[14] 冯元桢.生物力学:活组织的力学特征[M].戴克刚,鞠烽炽,译.长沙:湖南科学技术出版社,1983:194-224.
