小波变换在ADSP-BF533上的算法设计及实现
2010-02-23张伟,陈娟
张 伟, 陈 娟
(咸阳师范学院计算机科学系, 陕西 咸阳 712000)
0 引言
目前图像采集系统已广泛应用于银行、超市、楼宇等场合,在图像采集系统中选取合适的编码方式至关重要.作者选取了具有高压缩率、容错性较高、具有开放框架的JPEG2000[1]对采集的图像进行压缩编码,以提高网络对数据信息流量的需要.本系统中选用ADI公司Blackfin DSP系列产品之一的ADSP-BF533芯片作为处理单元,它同时完成图像信号的JPEG2000标准的压缩和信号的控制,并对小波变换用于ADSP-BF533上的算法进行了设计与实现.
1 ADSP-BF533芯片

图1 ADSP-BF533系统框图
ADSP-BF533是BlackFin系列芯片中性能较好的一种.ADSP-BF533具有600 MHz时钟频率和1.2 GMACS(每秒十亿次乘法累加运算)运算速度,该系列处理器在300 MHz时钟频率时功耗仅为0.15 mW/MMAC,ADSP-BF533在达到600 MHz性能水平时的功耗仅为280 mW.为了充分发挥BlackFin体系结构的动态电源管理能力,该系列处理器集成了一个片内开关稳压器,它利用2.25~3.6 V外接电源电压可产生0.7~1.2 V可设置的内核工作电压.从而降低了总体成本,并节省了外部电源元器件.ADSP-BF533的系统框图[2]如图1所示.
2 小波变换
小波变换是一种复杂的数学变换,可以在时域和频域上对原始信号进行多分辨率分解.对二维图像做小波变换,实际上就是把原始图像的像素值矩阵变换成另一个有利于压缩编码的系数矩阵,经过小波变换后,原始图像被分解成几个子图像,每个子图像包含了原始图像中的不同频率成分[3].
2.1 小波变换基础
二维 DWT是从一个一维基块中构造的,该基块可以将有限长度的输入序列x[n]转换为两个子带序列y0[n]和y1[n].前一个是低通子带,并且其构造可以理解为低通滤波,其后为子采样.y1[n]则是高通子带,相当于高通滤波,并跟随子采样.这两个子带序列中包含有与x[n]相同数目的样本[4].
y[n]的获得可以通过将低通和高通子带样本交织获得,其关系如式(1)所示:
y[2n]=y0[n],y[2n+1]=y1[n]
(1)
单个的“DWT”首先对一个二维序列(图像分量)x[n]的列独立地进行子带变换,然后再对行进行子带变换,产生4个子带y00[n]至y11[n].其中,x[n]=x[n1,n2]是一有限序列,n1和n2分别表示行与列索引.y[n]则为交织子带样本的二维序列,如式(2)所示:
y[2n1+b1, 2n2+b2]=yb1,b2[n1,n2],b1,b2∈{0,1}
(2)
这样y[n]具有与x[n]相同的支撑区域.在对图像进行压缩编码时,首先对x[n]的每个列运用一维子带变换,然后对其结果的每行进行一维子带变换,这样就可得到y[n].类似地,在解码的时候,为了从y[n]反变换到x[n],可首先对y[n]的每个行运用反向一维子带变换,然后对其结果的每列进行反向一维子带变换.
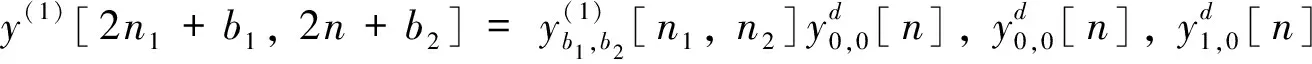
JPEG2000标准支持的D值范围在0≤D≤32,典型的范围为4≤D≤8.在实际开发中,D=5就可获得近于理想的图像压缩性能.对于压缩二值图像或者带调色板的彩色图像,此时可以设置D=0而跳过DWT操作,而由标准所规定的量化和编码操作直接对图像样本值x[n]进行.
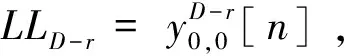
由单个DWT 级所产生的4个子带可以被交织到一个序列中去,用y(1)[n] 表示,如式(3)所示:
y(1)[2n+b1, 2n2+b2]=y(1)[n1,n2]b1,b2∈{0,1}
(3)
其中,y(1)[n]具有与x[n]相同的支撑区域.用这种方式组织子带样本的意义在于,它使得每个子带样本在原始图像支撑区域中占据一个唯一的位置,而这也是整个压缩过程中图像划分的基础.
2.2 不可逆小波变换和可逆小波变换
JPEG2000标准提供了许多小波变换核,但其中无论是可逆还是不可逆小波变换都只支持一种小波核.对于不可逆小波变换,JPEG2000只支持CDF 9/7核,低通和高通分析滤波器分别具有长度9和7,其表达式可近似如式(4)、式(5)所示:
低通:
949 018 236+0.266 864 118 443(z1+z-1)-0.078 223 266 529(z2+z-2)
+0.016 864 118 443(z3+z-3)+0.026 748 757 411(z4+z-4)
(4)
高通:
543 526 229-0.295 635 851 557(z1+z-1)-0.028 771 763 114 9(z2+z-2)
+0.045 635 881 557(z3+z-3)
(5)
这个核属于奇数长度线性相位小波中的Cohen-Daubechies-Feauveau 簇中的第一个.
可逆的DWT可以在与不可逆 DWT 完全相同的框架内实现,只不过它的分析和综合操作要由非线性操作来近似,这种操作必须能够有效地将整数映射到整数中.
可逆小波变换在JPEG2000第一部分中只支持5/3小波核,对应的低通和高通分析滤波器分别具有长度5和3,如式(6)、式(7)所示:
低通:
(6)
高通:
(7)
3 小波变换在ADSP-BF533上的算法设计及实现
3.1 带滤波器的离散小波变换
如图2所示为基于最单纯的对分子带滤波器的离散小波变换的分析与综合系统[5].这里,H0(z)、G0(z)为低通滤波器;H1(z),G1(z)为高通滤波器;↓2和↑2分别为2∶1抽取(down sampling)和1∶2内插(插入0值).此类方法包括倍频分解、树形分解和Mallat分解.基于表示此类方法的子带分裂次数的参数称为分解层次,图3为分解层次为2时对二维空间的子带分裂.
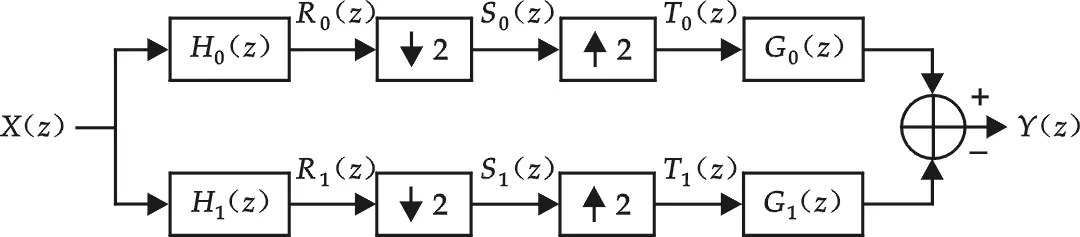
图2 基于最单纯的对分子带滤波器的离散小波变换的分析与综合系统
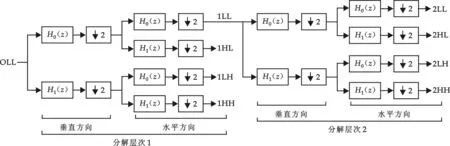
图3 分解层次为2时对二维空间的子带分裂
3.2 小波变换的算法设计
3.2.1 小波正变换的算法设计
离散小波正变换的输入为填充分量采样I(x,y)和分解层次NL,输出子带系数ab(ub,vb).具体实现步骤如下:
(1)输入填充分量采样I(x,y)和分解层次NL.
(2)将分解层次NL与当前层次lev比较,如果lev
(3)对输入数组的列进行一维小波正变换.
(4)将当前的分解列数u与数组最大列数ui比较,如果u
(5)对输入数组的行进行一维小波正变换.
(6)将当前的分解行数与数组最大行数比较,如果v
(7)进行二维系数的反交错处理.然后跳回第(2)步进行处理;程序流程如图4所示.
3.2.2 一维小波的实现步骤
(1)输入一维数组X和信号长度(i0,i1).
(2)信号长度和1进行比较,如果等于1,转(5)处理;如果大于1,转(3)处理.
(3)对一维数组X进行信号周期性扩展.
(4)对扩展信号Xext进行提升结构的小波变换.
(5)对i0进行判断,如果i0是偶数则进行低通输出;如果i0是奇数则进行高通输出,一维小波的流程图如图5所示.
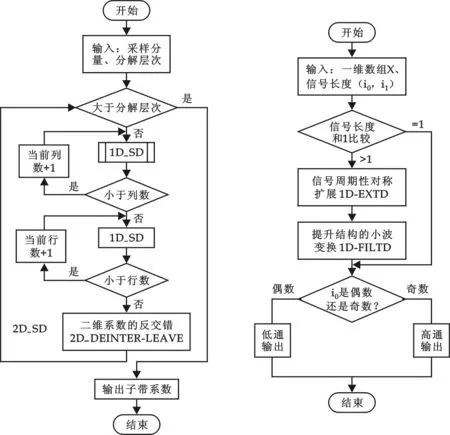
图4 小波正变换的程序总流程图 图5 一维小波程序流程图
上述算法在ADSP-BF533上进行了编程与实现,程序运行的硬件环境是EZ-KIT Lite(ADSP-BF533)板,软件环境是Vis/ualDSP++ Environment6.0.
4 结束语
从实验可以看出,在快速小波变换算法中只有加减操作和移位操作,占用硬件资源较少;对于16×16位图像数据块的JPEG2000可逆整数5/3一维小波变换只需784个指令周期,与其视频输出接口指令周期1 728相比还有较大的剩余空间,可见利用该DSP芯片处理图像,能达到图像处理的实时性要求,且图像处理质量高.小波变换在ADSP-BF533上的算法设计与实现为无线网络的进一步发展提供了可行的算法,具有较为广泛的应用价值.
[1] ISO/IECJTC1/SC29/WG1N505.Call for contributions for JPEG2000(JTC1.29.14,15444):image coding system[Z],1997: 28-39.
[2] http://www.analog.com/UploadedFiles/Associated_Docs/892485982bf533_hwr.pdf[EB/OL].
[3] 成礼智.小波的理论与应用[M]. 北京:科学出版社,2004: 230-232.
[4] 亢 琰.小波提升算法在JPEG2000可逆变换中的应用与实现[J]. 航海电子工程,2007,127(2):43-44.
[5] 陈武凡.小波分析及其在图像处理中的应用[M]. 北京:科学出版社, 2008:8-56.
