地面武装机器人发射动力学仿真与分析

倪文彬，王荣林

（南京理工大学泰州科技学院，江苏泰州225300）

机器人技术的发展，为地面武装机器人的设计和研究提供了良好的技术基础。研制地面武装机器人的目的，是减小人员伤亡，代替人在危险、恶劣的战场环境执行军事任务，例如侦察、作战、爆破等。该文设计了一种地面武装机器人，该机器人搭载了轻武器发射系统，可用来执行部分消防、反恐、防暴、灭火等危险作业。

1 系统构成与设计

本机器人系统分为移动车体平台及搭载平台两部分。在移动载体设计过程中，对移动机器人进行了传动系统、轮系结构以及底盘进行了设计。在确定了搭载平台自由度前提下，把搭载平台分成方向机和高低机分别设计。最终三维效果图如图1所示。

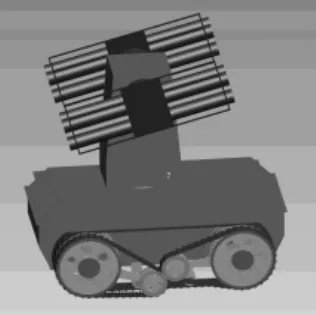
图1 移动机器人载体及搭载平台三维图

该武装机器人搭载平台自身携带的两个自由度，一个是绕垂直方向轴360°的旋转自由度，即方向机；另一个是绕水平方向轴±180°的旋转自由度，即高低机。通过这两个自由度，一般的发射性装置均能够完成指定任务。二维随动搭载平台的运动自由度示意图如图2所示。

图2 武装机器人搭载平台运动自由度示意图

2 系统发射动力学建模

2.1 系统描述

对该武装机器人系统进行动力学分析时，把车体、高低机、方向机、发射箱和弹分别设为刚体。为了便于研究，首先应确定系统的拓扑构型，对于任意多体系统的拓扑构型表达方式而言，每个个体记作 Bi（i=1，2，…，N），N 为系统中刚体的个数，铰用一条连接邻接刚体的有向线段表示，记为Hj（j=1，2，…），B0表示系统外运动为已知的刚体。刚体和铰按以下规则表示：

（1）与B0邻接的刚体记为B1；

（2）各刚体的序号大于其内接刚体的序号；

（3）各刚体与其内接铰有相同的序号；

（4）每个铰的指向一律背离B0方向。

根据此规定，机器人系统的拓扑结构可用图3的方式表达。

图3 多体系统拓扑关系

2.2 系统动力学方程的建立[1]

移动机器人系统动力学模型，是进行动力学分析的基础。

系统中各刚体坐标系的建立：

则在整个系统中，任一刚体Bi的坐标可表示为

刚体Bi的线速度和角速度可表示为

由式（2）知

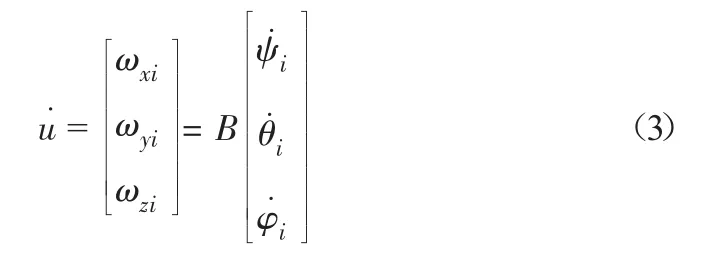
系统中任一刚体的平动动能为

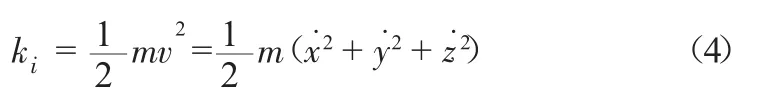
刚体的转动动能为

刚体Bi在惯性坐标系中的角速度为

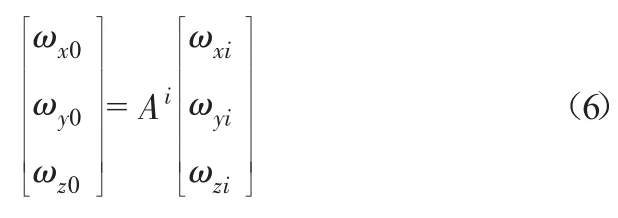
式（6）中，Ai为坐标变换矩阵。

将式（6）代入式（5），就可以得出刚体的转动动能。对于任一刚体，已知其固连坐标系的基点在惯性坐标系的位置和欧拉角，就可以求取其动能。

将以上的分级结果代入拉格朗日第一类方程

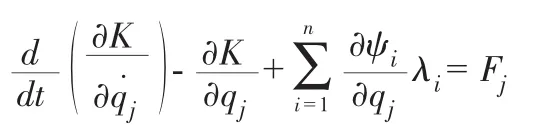
即可得系统的动力学方程

式（7）中，T为系统动能；q为系统广义坐标阵列；Q为广义力矩阵；ρ为对应于完整约束的拉氏乘子列阵；μ为对应于非完整约束的拉氏乘子列阵。

3 系统在ADAMS中的仿真

将Pro/E中建立的移动机器人系统三维实体模型导入ADAMS，对各零部件赋予质量属性，并用使用约束库中的约束，来模拟各零部件之间的连接，通过这些约束限制构件之间的某些相对运动[2]。移动机器人系统在ADAMS中模型如图4所示。

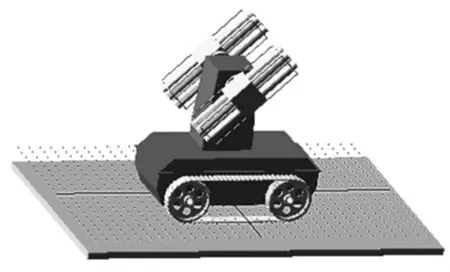
图4 移动机器人在ADAMS环境下模型图

3.1 齐次射击振动仿真

移动机器人系统的火箭弹，在发射过程中采取一次击发两枚对称火箭弹的方式，发射顺序根据先上后下、从外到内、左右交替或左右对称的原则，射击顺序如图5所示。

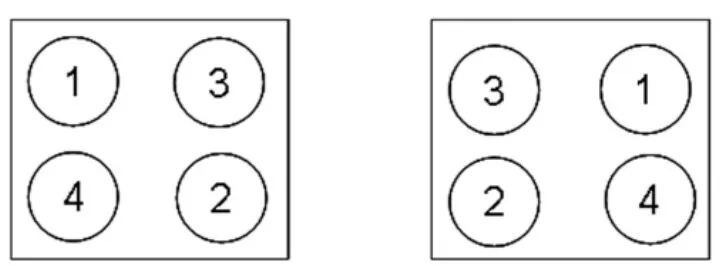
图5 射击顺序示意图

根据单次射击的结果，将齐次发射的射击间隔设为0.2 s。8发齐射的振动仿真结果如下各图所示。

（1）定向管位移时间函数（如图6～图8所示）。

（2）移动机器人载体位移时间函数（如图9～图11所示）。

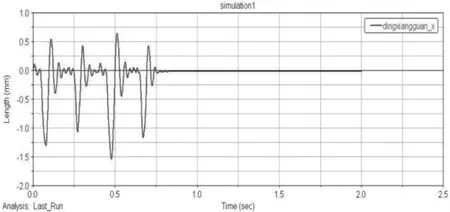
图6 定向管管口x方向位移

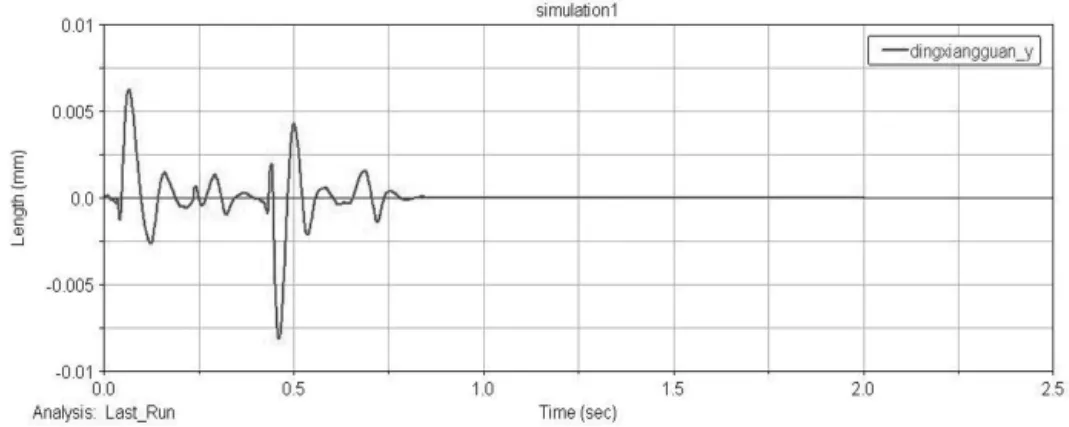
图7 定向管管口y方向位移

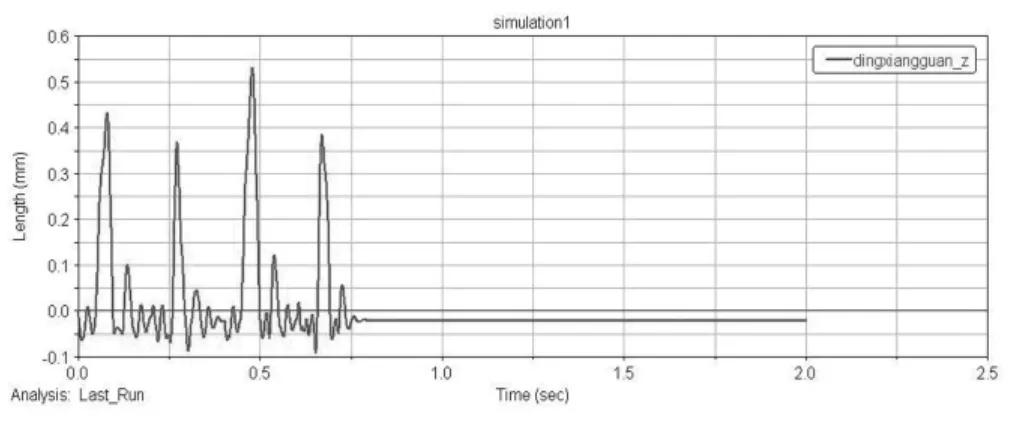
图8 定向管管口z方向位移

图9 移动机器人车体x方向位移

图10 移动机器人车体y方向位移

图11 移动机器人车体z方向位移

3.2 仿真结果分析

火箭弹被分为4组进行发射，因此定向器和车体出现了4次相似的振动变化。每个周期内的振动情况与单次射击时相似。火箭弹发射后，定向器和车体振动逐渐衰减，直到0.2 s后击发下一组火箭弹之前，影响火箭弹起始扰动的参数，会衰减到一较小的范围内，没有对下一组弹造成较大的振动累加。

4 结束语

通过对地面武装移动机器人系统建立发射动力学方程，在ADAMS中的建模，并对模型赋予质量信息，确定各部件的约束关系，根据发射的环境，对模型施加了合理的仿真载荷，对移动机器人发射系统进行了齐次发射仿真，确定了齐次发射的时间间隔，并制定了合理的齐次发射射序。通过发射动力学分析，为机器人的进一步优化设计提供了基础。

[1]刘又午，等.多体系统动力学[M].天津：天津大学出版社，1991.

[2]李增刚.ADAMS入门详解与实例[M].北京：国防工业大学出版社，2008.

[3]张中利，于存贵，马大为，柴华伟.火箭弹在定向管内碰撞运动的仿真研究[J].系统仿真学报，2007，19(4)：875-878.

[4]赵 岗，马大为，方 帆.基于起始扰动仿真的火箭炮动力因素匹配研究[J].计算机工程与设计，2007，28(19)：4743-4746.

[5]杨 帆，王国平，芮筱亭，李德成，李苏泷，姚志军.射击间隔对多管火箭动态特性的影响[J].南京理工大学学报，2006，30(4)：400-403.