基于即时学习策略的火电厂烟气含氧量软测量
2010-02-20张炎欣
张炎欣,张 航,王 伟
(中南大学信息科学与工程学院,湖南长沙410083)
电力生产是国民经济发展的先行军。虽然我国近年来在风力发电、光伏发电、核电等方面取得了长足发展,但目前火力发电仍占主导地位,其容量占总容量80%以上[1~2]。随着国民经济的高速发展和科学技术的进步,电力工业发展迅速,现代大型火电机组普遍采用大容量、高参数单元机组,生产技术达到了一定水平[3~4]。但在效益、环保等方面,同国家建设节约型社会的能源基本方针还存在很大差距[5]。
影响火电厂优化运行的一个重要因素,是许多重要的过程参数和经济指标难以在线实时检测。如烟气含氧量等,都是直接反映发电效率和运行安全的重要热工参数,由于管理体制和技术、经济等原因,没有进行实时准确的测量,严重制约了火电厂过程控制和优化运行技术的发展,降低了企业的发电效率、提高了企业的生产成本。因此,对烟气含氧量等热工参数进行实时、准确的测量具有重要的意义。
1 对烟气含氧量软测量的研究概述
针对锅炉燃烧过程烟气含氧量无法实时准确检测的问题,众多学者在分析煤质变化、锅炉炉膛漏风和未完全燃烧等因素对烟气含氧量影响的基础上,展开了烟气含氧量软测量模型的研究。
文献[6]提出基于一种由一个包含隐层的三层前向网络,和一个不包含隐层的线性前向网络并联组成的复合型神经网络,并将该复合型神经网络应用到火电厂烟气含氧量软测量,通过对不同负荷下实测数据的仿真实验,验证了该方法的有效性。
文献[7]采用燃烧机理分析以及统计分析方法,建立风量和给煤量的软测量模型。采用多传感器数据融合方法,并加以煤质校正等处理,得到一个完整的氧量软测量模型。通过仿真验证,建立的氧量软测量模型,能较好的反映烟气含氧量的变化。
文献[8]提出基于混合高斯过程的软仪表,利用期望最大算法,实现对混合模型中的参数估计。判断出与特定工况相关程度最大的过程知识,利用它们建立与特定工况对应的局部模型,并将它们合并组成具有多模型结构的全局模型。仿真结果表明,文中提出的方法能有效地实现工业过程参数的软测量,具有较大的实用价值。
文献[9]提出一种新型的基于支持向量回归算法的软侧量模型,利用训练数据性能信息获得模型训练参数,减少人为因素对模型精度的影响,以提高建模效率和模型精度。针对某火电厂历史实测数据仿真结果表明,文中提出的方法能有效实现热工过程参数的软测量,有较大实用价值。
文献[10]采用径向基核函数的最小二乘支持向量机建模方法,进行烟气含氧量的软测量,由于该方法中正则化参数和核函数宽度参数的选取,对预测模型精度影响较大,引入粒子群优化算法对进行上述两参数的寻优,基于实际检测数据的仿真结果表明,该方法具有较好的预测效果。
文献[11]针对常规建模方法,在实际应用中所面临的建模难题,提出了一种新的建模思想——反向建模方法,利用实际复杂热力系统运行时产生的大量实时数据,建立系统数学模型的学术思想。阐述了反向建模方法的思想、建模过程的模式。以烟气含氧量为例,利用华能福州电厂所采集的大量现场运行数据,选用偏最小二乘算法,利用反向建模思想,建立一个局部系统的数学模型,验证结果表明,该建模思想的有效性和实用性。
上述研究工作,有效推动了电厂烟气含氧量软测量的实际应用。但上述方法主要是基于全局模型的建模技术,建模过程中需要获得能够覆盖整个生产工况的运行数据,对于实际电厂生产过程而言,这是比较困难的;同时,随着电网调峰任务的加重,火电单元机组负荷变化更加频繁,针对不同工况下模型的在线自适应问题,上述方法没有进行很好的考虑,通常需要对模型从新进行离线校正,过程中需要过多的人为干预。因此,上述方法虽然在烟气含氧量软测量建模中取得了不错的应用效果,但是在建模理论方面和实际应用等方面,仍然有很多值得研究的地方。
针对电厂烟气含氧量难以进行实时有效检测的问题,从提高软测量模型在线自适应能力的角度出发,本文提出一种基于即时学习策略的改进支持向量机预测建模方法,并通过基于电厂实际运行数据的仿真实验,验证本文方法的有效性。
2 锅炉燃烧过程分析及辅助变量的确定
循环流化床锅炉具有燃料适应性广、低污染排放等优点,是国内外广泛推广的一种煤燃烧技术。它采用炉内物料循环燃烧,使得燃料能够燃烧充分,降低了燃煤电厂的能耗,并能够燃烧劣质煤,甚至煤矸石、生物质之类的燃料。循环流化床锅炉使用炉内脱硫法来解决减排问题,即通过炉内添加石灰石粉,经过循环燃烧,使得石灰石粉和煤的充分反应,来实现硫化物的固化,并通过低温燃烧来抑制氮氧化物的产生。循环流化床锅炉的主要组成部分有锅炉本体、给煤系统、一次风系统、二次风系统、分离器、回料器、尾部烟道、冷渣器等。
通过实际现场调研发现,烟气含氧量主要受煤质变化、锅炉炉膛漏风、未完全燃烧等因素的影响,从机理分析角度出发需要选择能反映负荷、燃料、风量、排烟等方面的变量作为辅助变量。因此,本文选取燃料量、主给水流量、主蒸汽流量、排烟温度、给水流量、高压主汽阀前压力、送风机入口风量、送风机动叶开度、引风机入口风量9个过程参数,作为烟气含氧量软测量模型的辅助变量。
3 基于即时学习策略的改进支持向量机软测量建模方法
即时学习策略,利用系统当前工况点,从历史数据库中寻找与当前工况点匹配程度最好的一系列数据,采用某种建模方法,建立当前系统的局部模型,并计算出系统的输出。与全局建模方法相比,由于即时学习模型的建立和优化是局部进行的,使得模型的预测误差更小,并且由于预测模型只是在查询工作点处产生,因此可以在线增加新的观测数据到数据库,或者从数据库中删除旧的数据,使模型具有较好的自适应能力。
即时学习模型的主要缺点,是建模消耗大,从而导致模型实时性不强。但是对于工况变化大,常规方法建立的静态模型随时间精度下降大的情况,采用即时学习模型,能够使测量精度有明显的改善。
3.1 基于距离和角度信息的即时学习算法
在即时学习建模方法中,根据当前输入样本点确定的建模邻域的大小,对模型预测精度有很大影响,本文同时考虑样本的距离和角度信息,利用加权策略实现这两种方法所蕴含的不同信息的集成,将其作为样本间相似性的量度,以获得与当前输入样本具有较高相似度的建模邻域数据。
设当前输入样本点和样本样本集中数据都为9维向量Xa=(Xa1,…,Xa9)T,Xi=(Xi1,…,Xi9)T,则当前输入样本点 Xa和样本样本集中数据Xi的距离和角度信息表示如下:

式中λ∈[0,1]为权系数,si的取值介于[0,1]之间,其值越大,表示Xa和Xi越相似。
(1)当 Xa与 Xi的夹角较大,即 cos(θi)< 0 时,则认为数据Xi与当前输入样本点Xa的相似性较差,从保证建模精度的角度考虑,丢弃该数据样本;
(2)当 Xa与 Xi的夹角较小,即 cos(θi)≥0 时,认为 Xi数据与当前输入样本点Xa的相似性较好,选用式(3)作为相似样本集的选择量度。
从式(3)可以得出,该相似性量度准则综合考虑了样本信息的欧式距离与角度信急,具有较好的相似信息挖掘能力。利用该公式可构造出当前输入样本点Xa的邻域Ωk,由于Xa和Xi越相似,则si的值越大,因此,邻域公式可以表示为

数据窗口h的大小,对局部模型的预测效果影响很大。窗口h值过大,会增加算法的计算开销,同时引起较大的估计偏差;窗口h值过小,会造成较大的估计方差,使模型的泛化能力下降。所以数据窗口h值的选取是相当重要的。
数据窗口h值的确定方法,大致可分为两类:
一是数据驱动方法,这类方法是参数化建模方法的直接扩展,其目的是通过极小化某一代价函数获得最优的数据窗口值;
二是Direct Plug-in方法,该方法通过求解偏差和方差分析的渐进线,得到数据窗口的最优值,但由于偏差量和方差量都是未知项,必须通过估计值来取代这两个未知量,以得到最优的数据窗口。
基于数据驱动的方法需要极小化某一风险函数,因此算法较为复杂,工业现场具体实施较为困难,本文根据一定的先验知识,通过对实验数据多次重复建模,人工确定最佳的局部模型数据样本集的大小,一般取在30~40之间。
3.2 改进支持向量机预测模型
支持向量机是统计学习理论基本思想的实现,它运用结构风险最小化原则,避免了神经网络等基于经验风险最小化建模方法存在的过拟合、局部极小等缺陷,已广泛应用于工业过程预测建模、系统辨识的领域。支持向量机预测模型的基本思想为:对于给定的样本数据集合,在高维特征空间中构造一个回归函数,其中的权系数向量和阈值可通过求解凸二次规划问题得到。针对优化问题中的目标函数,构造拉格朗日函数,把原始的凸二次规划问题转化为对偶问题,并引入核函数,避免使用非线性映射。于是原回归函数可转化为
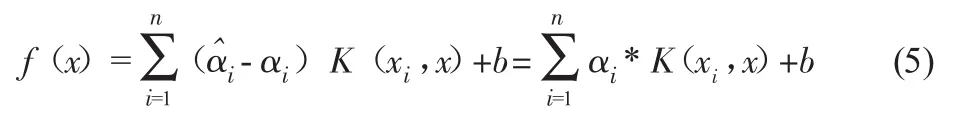
式中,
K(xi,xj)=准(xi)T准(xi)为核函数;
b为阈值,n为数据样本的组数。
在支持向量机建模过程中,正则化参数C则直接控制目标函数中的模型复杂度和训练误差的权重比例;不敏感参数ε控制不敏感带的宽度,影响支持向量机的稀疏性,一定程度上反映了对模型误差的容忍度;核函数K(xi,xj)隐式定义了低维变量空间到高维特征空间的非线性映射,对于RBF核而言,核函数的参数主要是核的宽度α2,它主要影响样本数据在高维特征空间中分布的复杂程度。上述3个参数选取的好坏,很大程度上决定了支持向量机预测模型的预测精度。
传统的参数选择方法,主要根据用户根据经验来选择模型参数,但这种方法带有很大的主观性,不能准确反映训练集对模型的影响。本文采用改进粒子群优化算法进行上述参数的寻优。
PSO算法在每一次的迭代中,粒子通过跟踪两个“极值”(pbest,i,gbest)来更新自己,其中pbest,i表示第i个粒子的个体最优值,gbest表示当前全局最优值。在找到这两个最优值后,粒子通过下式来更新自己的速度和位置

式中,
vi(k)是第i个粒子在第k次迭代中的速度矢量;
r1、r2是介于(0,1)之间的随机数;
c1和c2是学习因子,一般固定为2.0;
w表示惯性权重,采用下式获得

式中,
w0、w1为初始惯性权重;
Step为粒子群当前迭代的次数;
Gen为预设的总的迭代次数;
w值越大,其全局搜索能力越强;反之,w值越小,其局部搜索能力越强。
共轭梯度法是一个经典的非线性寻优算法,具有线性收敛的特点,其局部搜索能力较强。
设初始点 X(1),取 d1=-荦f(X(1)),
其中X(1)表示向量矢量;d1表示梯度负方向。
设 k ≥ 1,已得到 k 个相互共轭的方向 d(1),d(2),…,d(k),以及由X(1)开始依次沿上述方向精确一维搜索得到点X(2),…,X(k),X(k+1),即:

式中,λi表示通过某种线性搜索计算出的步长。
通过精确一维搜索,保证方向导数为0,即

在 X(i+1)点构造新方向 d(k+1)为 -荦f(X(k+1))与 d(1),d(2),…,d(k)的组合,由于 d(1),d(2),…,d(k)相互共轭,则有
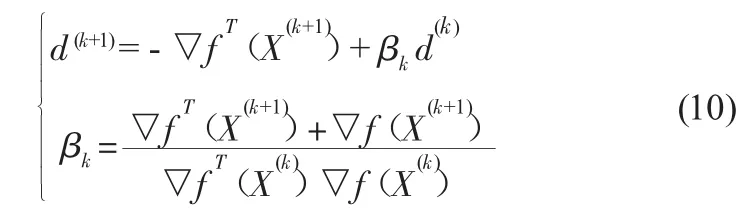
运用改进粒子群优化算法对SVM参数优化,选取的具体步骤如下所示:
(1)在给定范围内将SVM模型三个参数进行初始化,构成一个由三个浮点随机数组成的染色体,并进而形成初始种群;
(2)将种群中的个体解码,还原成SVM模型中的3个参数,并用训练样本集对SVM模型进行训练学习,以主导变量期望值和实际值的拟合误差作为寻优目标,这样种群中的每个个体都有一个适应度值,计算当代最佳粒子、全局历史最佳粒子和个体历史最佳粒子;
(3)判断算法是否停滞,若没有停滞,则继续执行粒子群算法,否则,对每个粒子产生一个随机数,如果该随机数小于0.1,则直接跳转到步骤(5),如果位于0.1和0.2之间,则对该粒子按照为一个小于1的随机数)进行变异后,再跳转到步骤(5);
(4)判断算法是否满足终止条件,若满足终止条件,则停止计算转到步骤(10),否则跳转到步骤(2);
(5)将粒子群优化算法得到的该粒子位置值赋给X(1),且d(1)=-荦f(X(1)),k=1;
(6)判断 ||荦f(X(k))||<ε?若小于,则转步骤(3),对下个粒子进行判断,否则进行下一步;
(7)求 min f(X(k)+λkd(k)),X(k+1)=X(k)+ λkd(k);
(8)k=n?,如果相等,则令 X(1)=X(n+1)、且 d(1)=-荦f(X(1))、k=1转步骤(6),如果不相等,则向下执行;
(9)d(k+1)=-f(X(k))+ βkd(k),k=k+1,转步骤(6)。
(10)将获得的种群中选择最优个体,解码还原得到SVM模型中的3个参数,建立相应的SVM模型,进行主导变量的预测建模。
3.3 预测模型的具体实现
为使算法具有较小的计算开销,采用加权模糊C均值聚类算法,对数据样本集进行聚类,利用两步搜索策略进行当前输入样本数据Xa相似数据集的选取。
首先,计算当前输入样本数据Xa与各个聚类中心的欧氏距离,找到与当前输入样本数据最近的一个聚类中心;
然后,在该聚类内部使用基于距离和角度信息的相似性公式进行局部模型样本数据的选取。同时对样本数据集的更新策略进行了相应的设计。采用上述方法建立烟气含氧量预测模型的具体过程描述如下:
(1)确定出能够覆盖锅炉燃烧过程各种工况的烟气含氧量预测模型输入输出数据样本集,数据样本集中的数据,都是从实际现场采集而来,并且经过过失误差和随机误差的消除,以及数据归一化处理等;
(2)确定加权模糊C均值聚类算法的初始聚类中心V(0)和阈值ε,计算得到带标记的l个聚类,并可确定每个聚类的聚类中心
(3)采用两步搜索策略,得到当前输入样本数据Xa(包含燃料量,主给水流量,主蒸汽流量,排烟温度,给水流量,高压主汽阀前压力,送风机入口风量,送风机动叶开度,引风机入口风量,共9个分量)的相似样本集Ωk;
(4)采用基于改进PSO算法的支持向量机预测模型,估计出当前输入样本数据Xa所对应的烟气含氧量y赞a;
(5)判断当前输入样本数据Xa是否为新数据,如果是,则对数据样本集中的数据进行聚类调整。
4 实际工业数据的验证分析
为进一步说明基于即时学习策略的改进SVM烟气含氧量预测模型的有效性,选取某月份的实际生产数据,经过数据预处理后得到500组有效数据,其中400组数据用于建模,另外100组数据用于算法校验。

改进PSO算法的种群规模定为pop=30,迭代次数为Gen=200,惯性权重变化范围为0.9~0.2,c1=c2=2。在每次局部SVM模型建立过程中,都采用改进PSO算法优化其C、σ、ε这3个参数,并用于该输入数据Xa下的烟气含氧量在线软测量。
为了说明本文算法的有效性,与采用采用标准BP神经网络和标准SVM方法获得的烟气含氧量预测建模进行对比分析。标准BP神经网络采用3层结构,输入节点数为9个,输出节点数为1个,隐层节点数设为23个。隐层神经元传递函数采用S型正切函数tansig,输出层神经元传递函数采用线性函数purelin。采用变学习率的前向误差反向传播学习算法训练BP神经网络,随迭代的进行,学习率η从0.9线性减小至0.1。标准SVM建模方法,采用径向基核函数,经过多次实验SVM预测模型中的3个关键参数取为C∈32.15,σ=0.25,ε=0.08。
图1至图3给出了标准BP神经网络、标准SVM和本文方法的烟气含氧量预测曲线。并采用MSE和MAPE两个指标作为量度,表1给出了三种建模方法的性能对比。其中MSE表示均方误差,MAPE表示平均绝对百分比误差,计算表达式为


图1 标准BP神经网络烟气含氧量预测曲线

图2 标准SVM烟气含氧量预测曲线

图3 基于即时学习策略的改进SVM烟气含氧量预测曲线

表1 三种建模方法性能统计表
由上图可知,标准BP神经网络、标准SVM和基于即时学习策略的改进SVM预测模型的预测值,与烟气含氧量实际检测值的变化都基本一致,但基于即时学习策略的改进SVM预测模型的跟随效果更好。通过表1可知,基于即时学习策略的改进SVM预测方法的均方误差和平均绝对百分比误差,比标准BP神经网络、标准SVM方法要明显小很多,表现出较高建模精度,但标准BP神经网络、标准SVM方法没有建模过程,因此其算法开销较小。对于烟气含氧量的预测过程而言,基于即时学习策略的改进SVM预测方法的计算开销是可以接受的,可以满足锅炉燃烧过程的实时性要求。特别地,随着时间的推移,锅炉的工况会发生缓慢的改变,使得采用标准BP神经网络、标准SVM方法获得的预测值误差越来越大,而采用基于即时学习策略的改进SVM预测方法,可以有效克服该问题,预测的烟气含氧量值比标准BP神经网络、标准SVM方法将更精确,模型的泛化能力也更强。
综合模型预测精度和锅炉燃烧过程对实时性的考虑,本文提出的基于即时学习策略的改进SVM预测方法,具有优良的建模性能,适合于建立烟气含氧量预测模型,烟气含氧量预测值能满足锅炉燃烧过程对烟气含氧量的误差要求。
5 结束语
本文针对电厂烟气含氧量难以进行有效预测的问题,从提高烟气含氧量预测模型在线自适应能力的角度出发,提出一种基于即时学习策略的改进支持向量机建模方法,并基于电厂实际运行数据进行了仿真研究。通过与标准BP神经网络和支持向量机等建模方法的比较,本文提出的烟气含氧量预测模型具有更好的预测性能,虽然算法的计算开销有所增加,但能够满足锅炉燃烧过程烟气含氧量预测的实时性要求,并及时为生产操作提供参考。
[1]姚之驹.2006年中国发电设备行业回顾及发展分析[J].电器工业,2007,(1):13-22.
[2]黄其励.我国清洁高效燃煤发电技术[J].华电技术,2008,30(3):1-8.
[3]李 波.火力发电机组超临界化的发展趋势[C].中国电机工程学会2004年学术年会论文集,北京:中国电力出版社,2004.
[4]李振中,吴少华,黄其励.超超临界燃煤发电机组的技术选择与产业化发展[C].中国电机工程学会2004年学术年会论文集,北京:中国电力出版社,2004.
[5]焦庆丰,朱光明,李 明,等.我国火电厂能耗现状及节能潜力分析 [J].湖南电力,2008,28(1):20-23.
[6]韩 璞,王东风,翟永杰.基于神经网络的火电厂烟气含氧量软测量[J].信息与控制,2001,30(2):189-192.
[7]赵 征,曾德良,田 亮,刘吉臻.基于数据融合的氧量软测量研究[J].中国电机工程学报,2005,25(7):7-12.
[8]熊志化,张卫庆,赵 瑜,邵惠鹤.基于混合高斯过程的多模型热力参数测量软测量[J].中国电机工程学报,2005,25(7):30-33,40.
[9]熊乔弘,周黎辉,潘卫华,陈 丽.基于参数自适应SVR的火电厂热工参数软测量[J].华北电力大学学报,2008,35(2):94-97.
[10]王宏志,陈 帅,侍洪波.基于最小二乘支持向量机和PSO算法的电厂烟气含氧量软测量[J].热力发电,2008,37(3):35-38.
[11]付忠广,靳 涛,周丽君,戈志华,郑 玲,杨勇平.复杂系统反向建模方法及偏最小二乘法建模应用研究[J].中国电机工程学报,2009,29(2):25-29.
