内置式永磁同步电机转子初始位置估计方法

王高林， 杨荣峰， 于泳， 徐壮， 徐殿国

(哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001)

0 引言

近年来，永磁同步电机调速系统逐渐成为交流传动领域的研究热点。按照永磁同步电机转子永磁体结构的不同，可分为表面式和内置式两种。内置式永磁同步电机(interior permanent magnet synchronous motor，IPMSM)的永磁体位于转子内部，转子磁路结构的不对称性将会产生磁阻转矩，对磁阻转矩进行控制，将有助于提高永磁同步电动机的过载能力和功率密度，从而可以拓宽调速范围，具有较广泛的应用领域。目前，研究低成本、强鲁棒性的无位置传感器IPMSM控制方法已成为交流电机控制技术的研究热点。无位置传感器IPMSM矢量控制方式下，所能产生的起动转矩大小取决于转子初始位置角的准确程度，如果初始位置角误差过大，将会导致电机在起动阶段带载能力受到限制，甚至会出现反转的现象［1］。因此，对于高性能无位置传感器IPMSM矢量控制系统，获取准确转子初始位置非常重要。

目前，已经有多种永磁同步电机转子初始位置估计方法相继被提出。较易实现的方法是基于定子铁心非线性饱和特性的原理，按照某种顺序注入一系列脉冲电压矢量信号来估计磁极位置，但实际电机结构的非理想性限制了其估计精确度［2］。针对内置式永磁同步电机，R D Lorenz首先提出了基于高频旋转电压信号注入的方法，可在静止状态下对转子磁极位置进行较准确地估计［3］。Sul Seungki提出了基于高频脉振电压信号注入的方法，目的是为了解决凸极效应不明显的表面式永磁同步电机(permanet magnet synchrouous motor，PMSM)磁极位置的估计［4］。传统高频旋转电压注入法是先提取负序高频电流分量，采用外差法或数字滤波等方法获取含有转子磁极位置信息的误差信号，然后通过龙贝格观测器估计磁极位置［1，5－6］。龙贝格观测器需要建立电机机械状态方程，涉及到电机转动惯量参数，并且需要对扰动转矩进行观测，然而很多实际应用场合中无法得知准确的电机参数。信号注入法需要对磁极极性进行判断，用于校正检测到的磁极位置［7］，可以通过提取二次高频正序电流分量来判断转子磁极极性［8］，但是由于二次高频正序电流信号的信噪比太低、算法比较复杂、对硬件电路要求较高。因此，有必要研究一种简单、可靠、实用的IPMSM转子初始位置估计方法。

本文研究一种基于混合信号注入的内置式永磁同步电机改进式转子初始位置估计方法，先通过注入高频旋转电压信号获取磁极位置角的初判值，然后将位置角初判值作为矢量角，注入2个方向相反的脉冲电压矢量来判断磁极极性，从而得到最终的转子初始位置角的估计值。最后，在一台22 kW内置式永磁同步电机进行实验验证。

1 转子磁极位置检测方法

采用高频旋转电压注入法对IPMSM转子磁极位置进行检测，其原理是利用IPMSM转子结构的凸极性，通过往定子绕组注入对称的三相高频旋转电压信号，将会在电机内产生旋转磁场，并在定子绕组感应出高频电流，然后通过信号处理从高频电流获取磁极位置角，如图1所示。

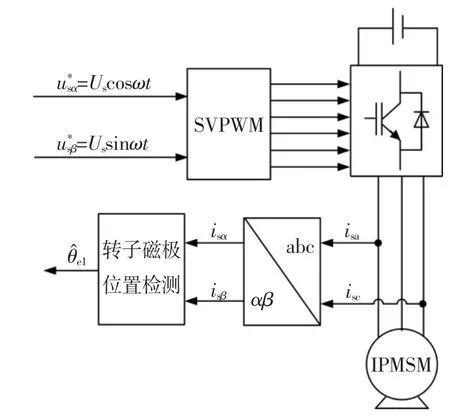
图1 高频电压信号注入框图Fig.1 Diagram of high frequency voltage signal injection

式中:Rs为定子电阻;p为微分算子;is和ψs分别为定子电流和磁链矢量，其中 ψs=Lsis+ ψfejθe，ψf为转子永磁体产生的磁链，θe为转子永磁体N极位置的电角度。

当所注入高频信号的频率ω远大于电机额定频率时，定子电阻将远小于高频感抗，高频电压模型(1)可以忽略阻抗压降，电压方程可近似表示为

如果电机在一个极距内只有一个空间凸极，则在同步旋转坐标系中，定子电感矩阵可以表示为

式中Ld和Lq分别表示d轴和q轴电感，对于内置式永磁同步电机，转子结构的凸极性使得Lq＞Ld。

在两相静止坐标系下，电感矩阵可以表示为

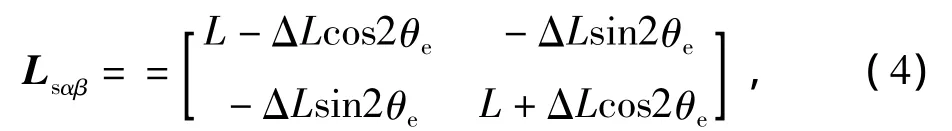
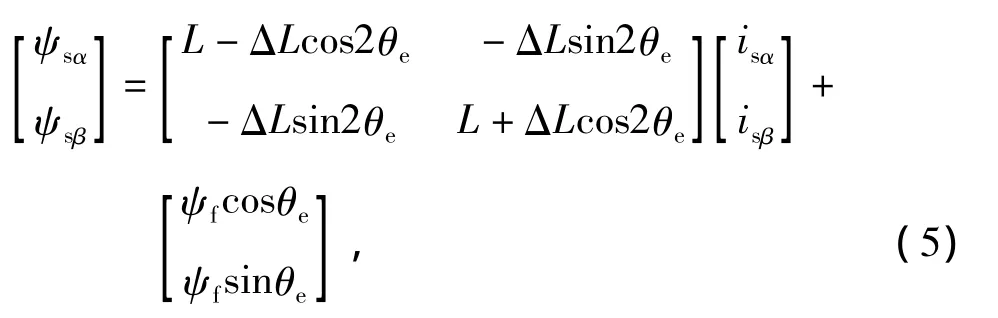
式中ψsα和ψsβ为两相静止坐标系下定子磁链分量;isα和isβ为两相静止坐标系下定子电流分量。

由于内置式永磁同步电机转子结构具有凸极性，所注入的高频电压将会在定子绕组上激励出含有磁极位置角信息的高频电流分量，由式(2)和式(5)可以得到高频电流在两相静止坐标系下的表达式，经化简可以得到

木雕艺术，历来都是世界工艺美术大家庭中的重要成员。历史痕迹、传统寄托、文化背景等多角度的特征，沉淀下独到的工艺特色和风格，洗练生动、生机盎然、包罗万象，美好意愿与艺术真谛存在于作品的细枝末节之中。至今，它们仍是当代木雕艺术家的学习范本与恒定的灵感来源。尽管历经不同的历史阶段，但都铭刻着各国人民内心世界的深层情感追求，以及对于文化脉络的传承与创造。它们是彰显人类思想、社会发展的物质媒介，给我们的审美观甚至是价值观都带来了潜在的改变。

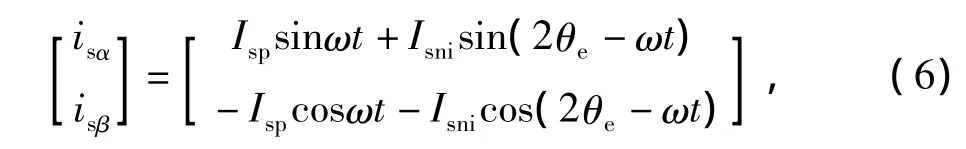
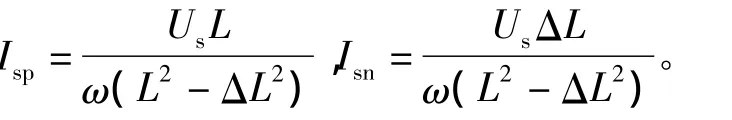
所产生的高频电流负序分量含有磁极位置信息，通过同步旋转滤波器滤除正序电流分量，提取出负序电流分量信号，再通过信号处理可以得到转子磁极位置的初判值，信号处理过程如图2所示。以ωt为旋转变换角，对 isα和 isβ进行旋转坐标变换，得到旋转坐标系下电流isdi和isqi，然后设计一个Butterworth二阶带通滤波器对其进行滤波，滤除正序分量和PWM载波噪声信号，得到负序分量isdn和isqn，经过坐标反变换，得到静止坐标系下的负序电流分量isαn和 isβn。于是，根据负序电流分量构造含有转子磁极位置误差信号εΔθe的表达式为

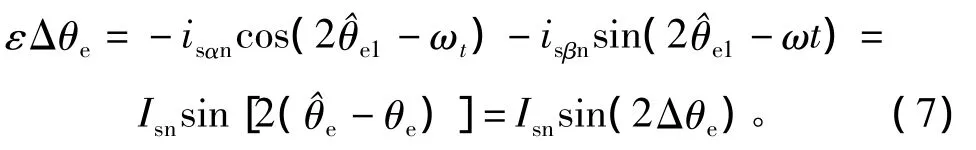
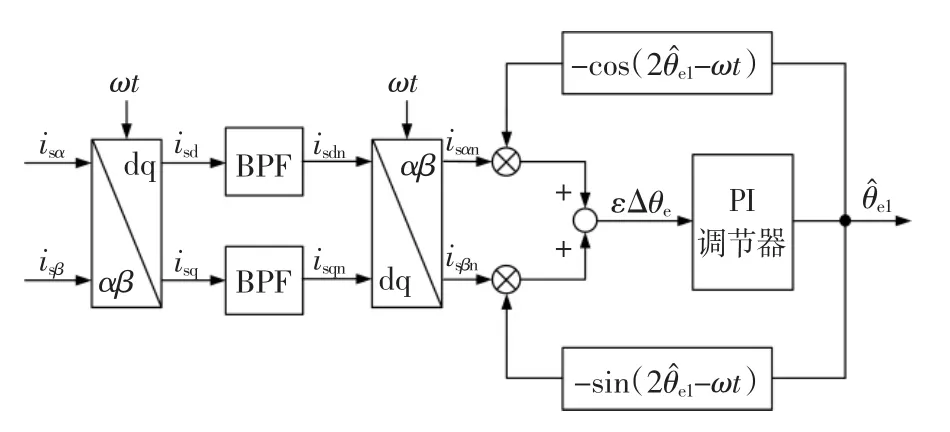
图2 磁极位置检测框图Fig.2 Diagram of magnet pole position estimation

当磁极位置辨识误差比较小时，εΔθe近似与Δθe成正比，为了降低估计算法的复杂程度，设计一个PI跟踪器对εΔθe进行调节，输出为转子磁极位置的辨识值。当εΔθe被调节至零时，辨识值也将收敛到实际转子磁极位置，获得转子磁极位置初判值。此时，表示的磁极位置可能是N极，也可能是S极，因此需要对转子磁极极性进行判断。

2 转子磁极极性判断方法

采用注入脉冲电压矢量的方法来判断所获得的初判位置角磁极的极性，脉冲注入法是基于定子铁芯非线性磁化特性来实现，其原理如图3所示。

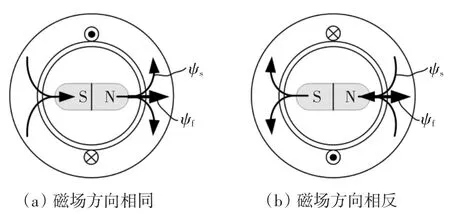
图3 基于定子铁心饱和特性辨识磁极极性原理Fig.3 Principle of polarity identification based on stator iron nonlinear saturation characteristic

在图3(a)情况下，当定子绕组电流产生的磁场ψs与转子永磁体磁场ψf方向一致时，气隙磁场等与上述2个磁场之和，即ψg=ψf+ψs，因此定子铁心磁饱和程度加大，磁阻变大，绕组电感将减小。在图3(b)情况下，当ψs与ψf方向相反时，2个磁场相互抵消，即ψg=ψf－ψs，使得气隙合成磁场变弱，定子铁心饱和程度降低，磁阻变小，绕组电感将增大。

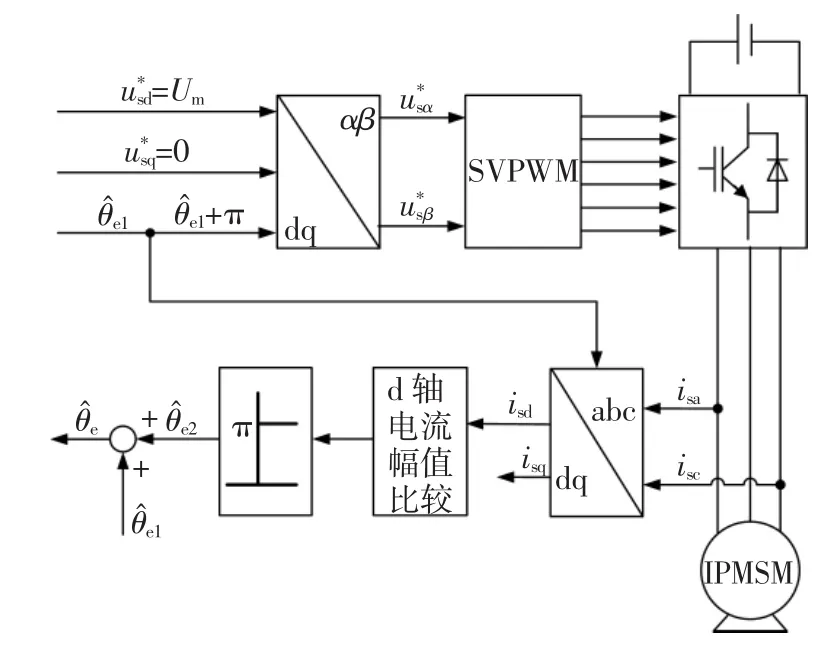
图4 转子磁极极性判断及补偿框图Fig.4 Diagram of rotor polarity identification and compensation

根据注入高频信号获得的磁极位置初判值，往定子绕组注入方向为和+π正反方向2个脉冲矢量，如图4所示。通过比较所激励直轴电流分量的大小，可以判断出磁极极性，当方向电压脉冲矢量产生的电流大于+π方向时，则表示N极位置，校正值=0;反之，校正值=π。

3 实验结果分析

采用无位置传感器转子初始位置角估计方法，对一台内置式永磁同步电机进行实验。电机参数为:额定功率22 kW;额定转矩210 N·m;额定电流37.2 A;额定电压380 V;额定转速1000 r/min;极对数3;定子电阻0.17 Ω;d轴电感5.5 mH，q轴电感7.2 mH。

采用TI公司的TMS320F2808 DSP来实现控制算法，逆变器开关管采用PM75RSE120功率集成模块，电流传感器采用HS-PHB60V4B15霍尔传感器，为了验证位置估计精确度，通过安装一个Heidenhain绝对式编码器(ECN 1113)来获取转子磁极实际位置，与估计值进行比较。DSP系统时钟设为100 MHz;PWM开关频率设为10kHz;所注入高频旋转电压的幅值为50 V，频率为1kHz;所注入脉冲电压矢量的幅值为190 V，脉宽时间为900 μs。

图5为实际转子位置角为45°时，注入高频旋转电压获取磁极位置角初判值实验波形，30ms后位置估计值已收敛到稳定值，为=50.3°。然后往定子绕组先后注入矢量角为50.3°和230.3°两个电压脉冲矢量，图6为实验测得d轴电流响应波形，第一个脉冲的d轴电流幅值大于第二个脉冲的d轴电流幅值，因此可以判断为N极的位置，不需要进行补偿，电角度估计误差为5.3°。

图7为实际转子位置角为300°时，注入旋转高频电压信号获取磁极位置角的实验波形，位置角估计值为=123.8°。然后往定子绕组先后注入矢量角为123.8°和303.8°两个电压脉冲矢量，图8为实验测得d轴电流的响应波形，第二脉冲的d轴电流幅值大于第一个脉冲的d轴电流幅值，可以判断为S极的位置，需要加上180°的补偿值，因此得到最终的转子初始位置角为303.8°，电角度估计误差为 3.8°。

图9为高频定子电流的李萨育波形，图9(a)和(b)分别为转子位置角为45°和300°时的波形，可以看出李萨育波形由正序分量和负序分量合成，椭圆轨迹的长轴为磁极位置方向，可以看出该方向包括磁极的N极和S极，因此检测出磁极位置之后，需要对极性进行判断。

图10为一个电角度周期内转子在不同位置时初始位置的估计结果，可以看出估计效果较好，电角度最大估计误差为10°，平均估计误差为4.6°。根据永磁同步电机矢量控制方式下的转矩方程式，在所述估计误差范围内可以产生足够的起动转矩，能够满足无位置传感器内置式永磁同步电机的起动要求。

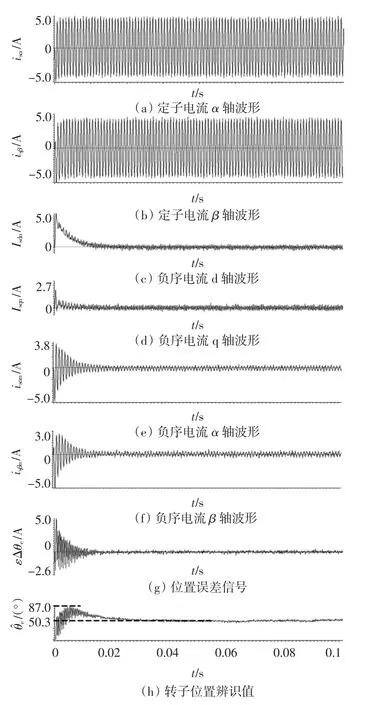
图5 高频信号注入实验波形 (θe=45°)Fig.5 Experimental waveforms of high-frequency voltage injection(θe=45°)

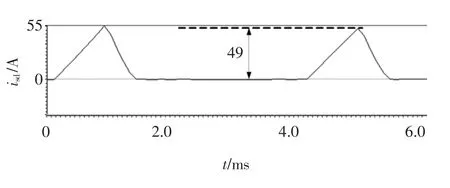
图6 脉冲电压注入实验波形 (θe=45°)Fig.6 Experimental waveforms of pulse voltage injection(θe=45°)

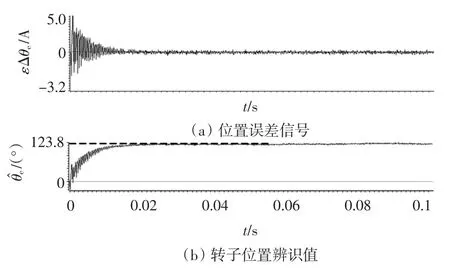
图7 高频信号注入实验波形 (θe=300°)Fig.7 Experimental waveforms of high-frequency voltage injection(θe=300°)

图8 脉冲电压注入实验波形 (θe=300°)Fig.8 Experimental waveforms of pulse voltage injection(θe=300°)

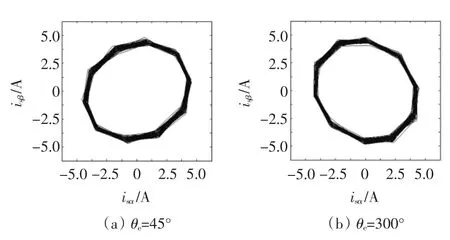
图9 定子高频电流实验波形Fig.9 Waveforms of high-frequency stator currents

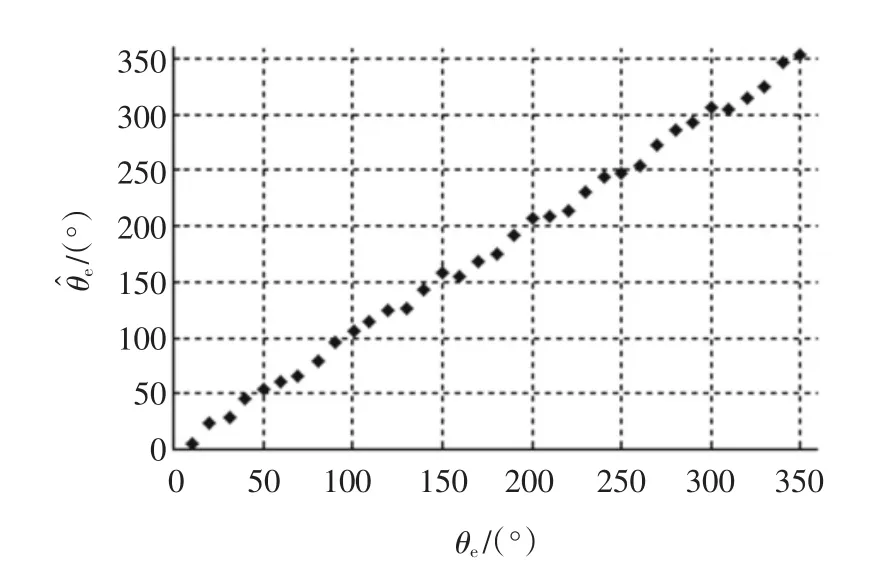
图10 转子初始位置估计实验结果Fig.10 Experimental results of initial rotor position estimation

4 结语

提出了一种基于混合信号注入的内置式永磁同步电机改进式转子初始位置估计方法。采用注入高频旋转电压信号的方法，提取出高频电流的负序分量，通过一个简单的比例积分跟踪器对构造的磁极位置误差信号进行控制，获取了磁极位置的初判值。在初判值的基础上，往定子绕组先后注入2个正反方向的脉冲电压矢量，有效地判断出转子磁极的极性，从而实现对初判值进行正确校正。实验结果验证了转子初始位置估计方法的有效性，所提出的方法简单、算法实现容易，可以用于解决无位置传感器内置式永磁同步电机的起动问题。

［1］贾洪平，贺益康.基于高频注入法的永磁同步电机转子初始位置检测研究［J］.中国电机工程学报，2007，27(15):15－20.JIA Hongping，HE Yikang.Study on inspection of the initial rotor position of a PMSM based on high-frequency signal injection［J］.Proceedings of the CSEE，2007，27(15):15－20.

［2］NAKASHIMA S，INAGAKI Y，MIKI I.Sensorless initial rotor position estimation of surface permanent-magnet synchronous motor［J］.IEEE Transactions on Industry Application，2000，36(6):1598－1603.

［3］CORLEY M J，LORENZ R D.Rotor position and velocity estimation for a salient-pole permanent magnet synchronous machine at standstill and high speeds［J］.IEEE Transactions on Industry Application，1998，34(4):784－789.

［4］JANG Jihoon，SUL Seungki，HA Jungik，et al.Sensorless drive of surface-mounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency［J］.IEEE Transactions on Industry Application，2003，39(4):1031－1039.

［5］JEONG Yuseok，LORENZ R D，JAHNS T M，et al.Initial rotor position estimation of an interior permanent-magnet synchronous machine using carrier-frequency injection methods［J］.IEEE Transactions on Industry Application，2005，41(1):38－45.

［6］王丽梅，郑建芬，郭庆鼎.基于载波注入的IPMSM转子初始位置估计［J］.电气传动，2005，35(3):20－22.WANG Limei，ZHENG Jianfen，GUO Qingding.Initial rotor position estimation of interior permanent magnet synchronous motor based on carrier frequency injection［J］.Electric Drive，2005，35(3):20－22.

［7］廖勇，沈朗，姚骏，等.改进的面贴式永磁同步电机转子初始位置检测［J］.电机与控制学报，2009，13(2):203－207.LIAO Yong，SHEN Lang，YAO Jun，et al.Initial rotor position detection for surface mounted PMSM based on rotating high frequency signal injection［J］.Electric Machines and Control，2009，13(2):203－207.

［8］RACA D，HARKE M C，LORENZ R D.Robust magnet polarity estimation for initialization of PM synchronous machines with near－zero saliency［J］.IEEE Transactions on Industry Application，2008，44(4):1199－1209.