游标时钟数字符合技术研究❋

孟升卫,黄灿杰,付 平,周 斌,方广有

(1.中国科学院 电子学研究所,北京 100190;2.哈尔滨工业大学自动化测试与控制研究所,黑龙江哈尔滨 150080）

时间间隔测量是信号周期、频率和相位等物理量测量的基础[1-2].常用的脉冲计数法测时分辨率为 1个时基周期 T base,采用时间内插的方法可获取小于 T base的分辨率[3-4].如图1所示,游标时间内插是基于游标卡尺的工作原理进行时间内插的[5].

在图1中有两个时钟信号,一个是主时钟,通常被用作时基;另一个时钟信号是游标时钟,两信号的周期为它们周期差值Δf的整数倍.时间内插的测量对象是主时钟信号上升沿与事件信号上升沿之间的时间间隔f,f＜T base.在游标时间内插过程,令游标时钟信号与事件信号同步,经过若干个周期,游标时钟与主时钟两个信号的上升沿将对齐,两时钟信号处于时钟符合状态.对游标时钟进行计数,根据到达符合状态所需的周期数可以计算出时间间隔f.时钟符合决定了游标时钟的计数终止时刻,对时间内插的精度有很大影响.

图1 游标时间内插原理示意图Fig.1 Principle of vernier tim e interpolation

图2 基于微分电路的时钟符合Fig.2 Differentiato r based coincidence circuit

1 基于微分电路的时钟符合

传统的游标符合方法是基于微分电路实现的,如图2所示,游标时钟信号的上升沿经过微分电路,在 D点产生一个正的窄脉冲,该窄脉冲经过整形到达 A点,两个时钟信号对应电路相同.当两个时钟的上升沿重合在一起时,A点和 B点全部为逻辑高,C点为逻辑高,表示处于符合状态;反则反之[5-6].图2中 D处和 E处的窄脉冲宽度由电路中电容C1,C2和电阻 R1,R2取值决定,窄脉冲宽度设置非常关键.如果D处和E处的窄脉冲宽度比或门 U1,U2的输入最小脉宽窄,U1,U2无法识别窄脉冲,导致应该符合而未能符合.如果D处和E处的两路窄脉冲太宽,符合电路的分辨率就会降低,导致许多误符合情况发生[7].

2 基于数字电路的时钟符合

符合状态是指两个信号的沿对齐状态.假定主时钟上升沿时刻为 tM,游标时钟上升沿时刻为 tV,分辨率为Δf,若 -Δf＜tM-tV＜Δf,则认为两时钟信号处于符合状态.下面分别在连续时间系统和离散时间系统中,对游标时间内插过程进行数学推导.

2.1 连续时间系统中游标内插的数学模型

式中:W(t)为冲激函数;W(t-jTbase)对应上升沿;-W(t-(j+0.5)Tbase)对应下降沿.假设主时钟上升沿(时刻 0)与事件信号上升沿之间间隔为f,游标时钟信号与事件信号同步,游标时钟信号 V(t)周期Tbase-Δf,Δf=Tbase/N;N为整数,且 N＞＞1,对游标时钟信号微分有

如果在 t到 t+Δf之间存在游标时钟上升沿和主时钟上升沿,则 C(t)=2.由 M(t)和 V(t)的周期可以看出 C(t)的周期 TC=N(N-1)Δf.若 t＜TC,且 C(t)=2,则有 k=int((t+Δf)/Tbase);int为取整操作,使得 -Δf≤k(Tbase- Δf)+f-kTbase≤Δf即

式 (5)从理论上说明了基于微分的时钟符合原理.但是传统的微分符合技术是通过电平信号的组合逻辑来反映符合状态,符合电路组合逻辑对输入电平信号的持续时间提出了苛刻的要求,对应式 (5)中的Δf必须要大于符合电路组合逻辑所能识别的最小时间,从而限制了游标内插分辨率的提高.

2.2 离散时间系统中游标内插的数学模型

为了进一步提高游标内插分辨率,将Δf=Tbase/N作为单位时间,对时间离散化.在时域离散系统中,主时钟信号周期为N.假定 i≥0,i为整数,式 (1)转换为

同理,游标时钟信号周期为 N1=N-1,与事件同步.假设事件上升沿时刻为 k,当 i＞k时,定义 N2=int(N 1/2),对于游标时钟作后向差分有

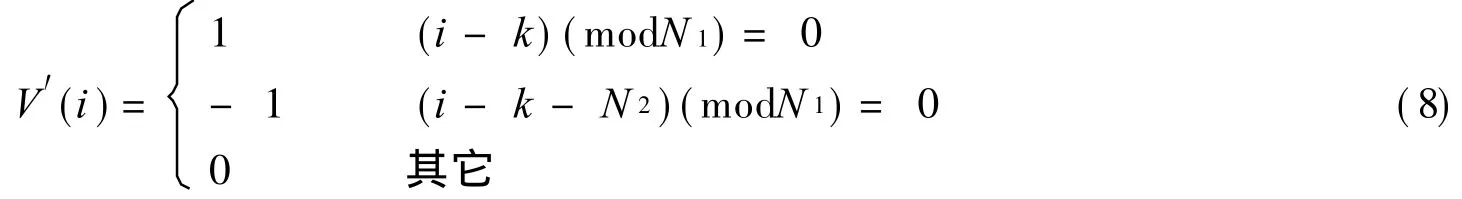
当式 (7)和式 (8)的值同时等于 1,表明两个时钟信号处于符合状态,此时i满足如下同余式组

由于 N≫1,N和 N-1互质,由中国剩余定理[8]有

式中:N1,N 2是衍数;a1,a2是乘率.由于 N 1=N≡1(mod(N-1)),故有 a1=1,化简式 (10)可得

通过主时钟信号与游标时钟信号的符合,可以确定式 (11)中的 i,从而可得到 k.

2.3 数字符合方法

根据式 (7)和式 (8),如果采样周期为Δf,采用直接采样的方法可以确定符合状态.但在实际的游标内插电路中,主时钟周期 Tbase=NΔf,游标时钟周期 TV=(N-1)Δf,不存在周期为Δf的时钟信号,采样只能基于主时钟或游标时钟进行.将式 (6)和式 (8)相乘,可得如下序列

通过上述理论分析,采用游标时钟信号对主时钟信号进行采样可保证 i满足式 (13),判断相邻两次的采样结果是否满足式 (14),从而可确定两个时钟信号是否处于符合状态.基于这种思想,本文设计了数字符合方法,图3为信号流程示意图,图中下方‘-1'

表示逻辑取反操作;零阶采样保持将游标时钟对主时钟采样结果保持 N-1个状态,即 1个游标时钟周期;z-1代表单位延迟,即 1个 Δf,由游标时钟周期 TV=(N-1)Δf可看出,z-(N-1)表示的延迟时间为 1个游标时钟周期;C(i)为两输入信号的逻辑与;C(i)=1表示两个时钟处于符合状态.

在数字符合方法中,检测到两个时钟处于符合状态的时刻比真正符合时刻晚了 1个游标时钟周期,与基于微分的方法相比,耗时长.但数字符合是利用采样进行符合状态判断的,两个时钟信号上升沿之间的时间差不受组合逻辑输入信号最小时间限制,因此分辨率可以进一步提高,符合精度与两个时钟信号的稳定度及采样精度有关.

3 仿真实验

为了验证所提方法,分别对基于微分电路的时钟信号符合方法和基于相位数字化的时钟信号符合方法进行了 Pspice仿真.基于微分电路的时钟符合仿真电路和图2一致,图2中 U1,U2选取 74F32,U3选取 74F08,延迟时间为 3 ns.游标时钟信号和主时钟信号分别采用 Pspice模型库中标准的数字激励(DSTM)产生,DSTM产生的数字信号驱动电流非常大.为了使仿真逼近实际电路工作情况,DSTM的输出经过 74F系列逻辑驱动后作为游标时钟信号和主时钟信号送至时钟符合器.

在对基于微分电路的时钟符合仿真过程中,经过大量的仿真测试,图2中的微分电容选择 45 pF,电阻选择 300Ω.电容电阻值的选择依据是使 D和 E处的脉冲宽度尽量窄,否则将会造成误符合,即两个时钟信号相差很大,但符合结果仍输出为 1.但是当 D和 E处的脉冲宽度窄到一定程度时,整形电路无法识别此模拟信号,A和 B处不能输出逻辑 1,无法反映符合状态.图4是 C=45 p F,R=300Ω情况下基于微分的时钟符合波形图,其中 A,B,C,D和 E分别对应图2中的相应位置.D和 E处的电压反映了游标时钟和主时钟信号经过微分电容后的幅度,A和 B处的信号为 D和 E处模拟信号整形后的数字信号.当 A和 B处均为逻辑 1时,C处输出逻辑 1,代表两个时钟信号达到符合状态.

在图4(a)中,两个时钟信号上升沿相差 1.8 ns,A和 B处有 D和 E处模拟信号整形后的数字输出,但 C处无符合输出.图中数字输出波形的后部有一段逻辑 1和逻辑 0的重叠区,此部分为数据不稳定区.在图4(b)中,两个时钟信号上升沿相差 1.7 ns,从符合结果C的波形图可以看出,两个时钟信号可以符合.表明该方法的分辨率为 1.7 ns.另外该方法对阻容的取值要求很严.由于这种符合方法最终的符合判据是对电平信号的判定,从电路实现中可以看出,符合信号是两个微分输出的电平信号逻辑与,门电路对输入脉宽有要求,无法进一步提高符合精度[7].若考虑电容、电阻的不确定性,基于微分电路的符合电路设计更为困难.

图4 基于微分电路的时钟符合波形图Fig.4 Clock coincidence results of differen tiator circuits

针对所提出的数字符合方法进行仿真,仿真电路如图5所示.图5与图3所示的信号流程图一致.在 Pspice仿真过程中,图5中的触发器采用 74F74,74F74带有反相输出,与门采用 74F08.为了消除电路亚稳态干扰,图5中的符合输出又经过游标时钟的负跳沿进行锁定.仿真结果如图6所示.

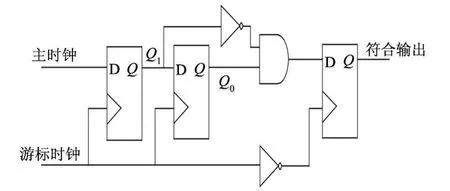
图5 数字符合方法电路图Fig.5 Coincidence circuit based on digital circuits

图6 数字时钟符合的 Pspice仿真波形图Fig.6 Digital clock coincidence w aveform in Pspice

在图6中,M1是主时钟信号,V1,V2和 V3为三个初始相位不同的游标时钟,C1,C2和 C3分别是三个游标时钟信号与主时钟信号符合输出.图6中的 M1初始相位(第一个上升沿)为 20 ns,周期为 20 ns;游标时钟周期为 19 ns,V1,V2和 V3的初始相位分别为 24 ns,25 ns和 23 ns,C1,C2和 C3分别在三个不同的周期内呈现高电平,说明数字时钟符合方法的分辨率可以达到 1 ns.由于数字时钟符合方法采用游标时钟信号对主时钟信号进行锁定,在图5所示的电路中采用了消除电路亚稳态干扰,符合结果的输出会晚半个游标时钟周期,不考虑 D触发器的传播延迟,符合结果的输出时刻比实际情况晚 10 ns左右;在实际的电路中,考虑 D触发器(如 74F74)的传播延迟,符合结果的输出时刻比实际情况晚 13 ns左右.

4 结 论

从仿真实验中可看出,数字时钟信号符合的误差取决于游标时钟和主时钟的周期差.在仿真中,两个时钟信号的周期差为 1 ns,时钟信号符合的最大误差不会超过 1 ns.从仿真结果可以看出,数字时钟符合方法优于基于微分电路的时钟符合方法.

[1] 张延,黄佩诚.高精度时间间隔测量技术与方法[J].天文学进展,2006,24(1):1-15.

Zhang Yan,Huang Peicheng.High-p recision time-interval measurement techniques and m ethods[J].Progress in Astronom y,2006,24(1):1-15.(in Chinese)

[2] 辛明,冯清贤.提高时间参量量化精度的方法[J].电子信息对抗技术,2006(5):22-24.

Xin Ming,Feng Qingxian.Amethod for precision time parametermeasurement[J].ElectronicW arfare Technology,2006(5):22-24.(in Chinese)

[3] 端木琼,刘常杰.基于 FPGA的高分辨率时间数位转换器设计[J].现代科学仪器,2008(5):33-35.

Duan Muqiong,Liu Chang jie.A design for FPGA-based time-to-digita l converter w ith high resolution[J].Modern Scientific Instruments,2008(5):33-35.(in Chinese)

[4] Jian Song,Qi An,Liu Shubin.A high-resolution time-to-digital im plemented in field-p rogrammab le-gate-arrays[J].IEEE Transactions on Nuclear Science,2006,53(1):236-241.

[5] 朱恒宝.游标法时间间隔测定器 [J].华东船舶工业学院学报,1997,11(2):90-97.

Zhu Hengbao.Time intervalmeasuring instrum ent based on vernier method[J].Journal o f East China Shipbuilding Institute,1997,11(2):90-97.(in Chinese)

[6] 陈堂敏,丁广壁.一种游标式测频的新方法[J].仪表技术,1999,3:32-34.

Chen Tangm in,Ding Guangbi. A novel method for frequency measuring with vernier[J].Instrumentation Technology,1999,3:32-34.(in Chinese)

[7] 刘莉,李署坚,邵定蓉.一种基于 FPGA用游标法实现的时间间隔测定器[J].遥测遥控,2005,5:63-67.

Liu Li,Li Shujian,Shao Dingrong.Tim e intervalmeasuring instrument based on FPGA with vernier method[J].Journal o f Telemetry,Tracking,and Command,2005(5):63-67.(in Chinese)

[8] 张顺燕.数学的源与流[M].北京:高等教育出版社.2000:215-266.