可调数学形态学的角点检测新算法

赵钦君，赵东标

(1. 南京航空航天大学自动化学院 南京 210016; 2. 南京航空航天大学机电学院 南京 210016)

可调数学形态学的角点检测新算法

赵钦君1，赵东标2

(1. 南京航空航天大学自动化学院 南京 210016; 2. 南京航空航天大学机电学院 南京 210016)

提出了一种新的基于可调形态学的角点检测方法。该方法采用对称圆形结构元素，通过选择合适的可调参数，对图像进行可调膨胀和可调腐蚀等一系列运算，先分别计算图像中凸角点和凹角点的精确位置，再将两者结合起来，从而得到图像中的所有角点。利用圆形结构元素大幅度减少了算法的计算量。可调形态学的应用克服了传统形态学检测角点不准确的缺点。实验结果证实了当可调算子中的参数取合适值时，该方法可以较精确地检测出图像中的角点位置。

角点检测; 膨胀; 腐蚀; 数学形态学; 结构元素

角点是图像的一种重要局部特征，它以极少的数据量保留了图像的重要特征信息，而且角点对透视变换、旋转及变形都具有鲁棒性，利用角点特征可以显著地提高立体视觉匹配和三维重建算法的效率，因此，角点检测在图像匹配、机器视觉、模式识别及三维重建中具有重要意义。

目前的角点检测技术可以分为基于边缘信息的角点检测、基于灰度信息的角点检测和基于模板的角点检测3类。基于边缘的角点检测算法把角点定义在图像边缘上，通过对边缘的特征进行分析提取角点。该算法检测出的角点对边缘线依赖较大，如果边缘线由于某种原因发生中断，则会对角点的提取结果造成影响。目前具体的检测算法有：基于边界链码的角点检测、基于边界曲率的角点检测、基于小波变换的角点检测[1-2]等。基于灰度信息的角点检测主要通过计算曲率及梯度达到检测角点的目的，如Harris算法[3]、SUSAN算法[4]。但其存在的问题是没有考虑多尺度的因素，计算出的局部极值点与角点的真实位置有很大的偏移。为解决角点检测的边缘依赖问题，基于模板的方法采用了基于区域的检测策略。该类方法一般预先定义角点模板，对图像中的各个区域进行比对，将与模板相似的区域的顶点作为角点。一般来说，该类方法的计算量较大，模板的设置经常依赖于人为经验，人为因素很大程度上决定了角点检测结果的好坏。

近年来，作为模板方法的一种，数学形态学方法[5]开始应用于角点检测中，为了达到检测的方向无关性，文献[6]用了4种不同的结构元素检测角点，使计算复杂度大幅提升，不利于实际应用。本文针对结构元素的旋转问题采用了圆形结构元素检测角点，有效减少了算法的计算量。很多文献[7-9]用传统的形态学基本算子如腐蚀、膨胀、开运算、闭运算等检测角点，但检测出的角点较模糊，不能精确到像素级。由于传统形态学运算对噪声和图像边界的细小凹凸较敏感，文献[10]提出了可调形态学并将其应用于图像处理与分析，文献[11]将其应用于角点检测，但检测出的角点不精确。本文提出了一种基于可调形态学的新的角点检测算法。该方法充分利用可调形态学的特点，通过选择合适的可调参数，对图像进行可调膨胀和可调腐蚀等一系列运算，先计算出图像中凸角点的精确位置，再计算图像中凹角点的精确位置，最后将两者结合起来，从而得到图像中的所有角点。同时，算法中圆形结构元素的应用，避免了由于旋转结构元素带来的额外计算开销，提高了算法的检测速度。实验结果表明，该算法克服了已有的形态学角点检测算法检测出的角点不精确的缺点，使检测出的角点可精确到像素级。

1 数学形态学及可调数学形态学

数学形态学是建立在集合代数基础上，用集合论方法定量描述几何结构的科学，被称为“惊人的数学”。最基本的形态学算子有膨胀(dilation)、腐蚀(erosion)、开启(opening)和闭合(closing)。

本文假设#B<∞。当 =1时，可调形态学运算即为传统形态学运算，所以，传统形态学可看作可调形态学的特殊情况。通过调整可调参数 ，可以克服传统形态学运算对噪声和图像边界的细小凹凸较敏感的缺点。可调膨胀(腐蚀)是关于约束量s递减(递增)的。假定结构元素反转不变，当约束量 增长时，可调膨胀(腐蚀)可以变成可调腐蚀(膨胀)，即可调膨胀(腐蚀)受约束过量的话，就会变成可调腐蚀(膨胀)。所以，可调腐蚀和膨胀在本质上是一致的。当#B=m时：

2 基于可调形态学的角点检测

为克服由旋转结构元素带来的运算成本过高问题，降低算法的计算量，提高算法的角点检测速度，本文采用如图1所示的5×5的圆形结构元素B对图像进行处理，结构元素B的基为21。

图1 结构元素B

通过运用可调形态学算法对图像的处理试验，总结基于可调形态学的角点检测算法步骤如下：

(1)约束参数 取一定的值，先对原始图像进行可调膨胀，然后对膨胀后的图像进行可调腐蚀，最后用所得的图像与原始图像进行比较，取两幅图像的差的绝对值作为角点集C1：

(2)用同样的结构元素，取同样的约束参数，先对原始图像进行可调腐蚀运算，再对腐蚀后的图像进行可调膨胀运算，最后用所得的图像与原始图像进行比较，取两幅图像差的绝对值作为角点集C2：

文献[11]取角点集C1和C2的并集作为所求角点。该方法检测出的角点很不精确，不能反映出角点的确切位置，特别是将文献[11]的方法对较尖锐的角点进行检测时，其对角点检测的不精确性体现得尤为明显。而本文给出的方法，充分发挥了可调膨胀和可调腐蚀不同的级联方式对检测图像中凸角点和凹角点起到的效果不同的特点，通过选择合适的可调参数，可将检测出的角点精确到像素级。

3 实验结果及分析

采用本文提出的角点检测方法对图像进行角点检测的试验结果如图2所示。其中图2a为输入图像，图2b、图2c、图2d、图2e为当可调参数 分别取2、8、14、19时所得的角点集C1。

由图2可见，当 较小时，对凸角点的检测特别是尖锐凸角点的检测较准确，而对凹角点的检测并不精确。这是因为 较小时，相当于可调膨胀和可调腐蚀的级联，可以把比结构元素小的缺口或孔填充上，但由于结构元素比较大，所以对凹角点填充的像素较多，致使对凹角点检测不精确；随着 的增大，对凸角点特别是尖锐凸角点的检测越来越不精确，这是因为 较大时，相当于可调腐蚀和可调膨胀的级联，可以把比结构元素小的突刺滤掉，由于结构元素比较大，所以滤除的突刺所占的像素较多，但此时对凹角点的检测还是比较精确的。因此，将两者结合起来即可检测出较精确的角点。

图2 角点集C1

当 取不同的值时，利用本文算法最终所得的角点集C，分别如图3所示。

由图3可见，当 =2时，有的角点检测不出来，而当 =4时，检测出的角点有些不够精确，达不到像素级。所以本文算法中 =3。

图4为用文献[11]的算法所得的角点集，由图可见，图3中本文算法检测出的角点更精确，特别是对于较尖锐角点的检测。

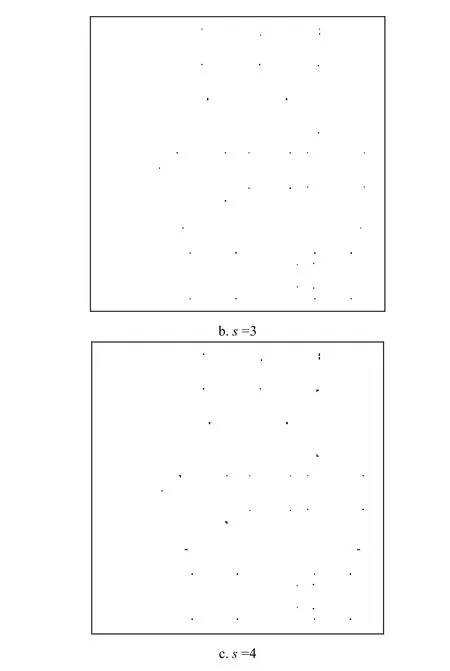
图3 角点集C

图4 文献[11]的算法所得角点集

4 结 束 语

本文提出了一种新的基于可调形态学的角点检测方法。该方法使用对称的圆形结构元素，避免了由于旋转结构元素带来的额外计算开销，提高了算法的检测速度。该方法克服了传统形态学检测角点不准确的缺点。由以上分析和实验结果可知，本文算法中 s ∈ [1 ,(m + 1 )/2]，当 太小时，所得的角点精度高，但有的角点检测不出来；而当s>4时，随着s的增大，检测出的角点越来越不精确，因此本文建议 取3附近的值。通过实验结果可以看出，当结构元素中的可调参数 =3时，与已有的形态学角点检测算法相比，该算法检测出的图像中角点的位置更精确。

[1]GAO X, SATTAR F, VENKATESWARLU R. Multiscale corner detection of gray level images based on Log-Gabor wavelet transform[J]. IEEE Trans on Circuits and Systems for Video Technology, 2007, 17(7): 868-875.

[2]GAO X, SATTAR F, VENKATESWARLU R. Corner detection of gray level images using gabor wavelets[C]//The IEEE International Conference on Image Processing.Singapore: IEEE, 2004: 2669-2672.

[3]HARRIS C, SATEPHENS M J. A combined corner and edge detector[C]//In Alvey Vision Conference. Manchester: [s.n.],1988: 147-152.

[4]SMITH S M, BRADY J M. SUSAN—a new approach to low level image processing[J]. Internetional Journal of Computer Vision, 1997, 23(1): 45-78.

[5]JIN Q. A novel adaptive approach to process binary fingerprint images using directional morphological operations[J]. Journal of Electronic Science and Technology of China, 2009, 7(2):129-132.

[6]LAGANIERE R. A morphological operator for corner detection[J]. Pattern Recognition, 1998, 31(11): 1643-1652.

[7]SOBANIA A, EVANS J P O. Morphological corner detector using paired triangular structuring elements[J]. Pattern Recognition, 2005, 38(7): 1087-1098.

[8]DINESH R, GURU D S. Corner detection using morphological skeleton: an efficient and nonparametric approach[M]. Heidelberg: Springer, 2006.

[9]CHANG Xing-zhi, GAO Li-qun, LI Yang. Corner detection based on morphological disk element[C]//Proceedings of the 2007 American Control Conference. New York, USA: [s.n.],2007: 1995-1999.

[10]AGAM G. Regulated morphological operations[J]. Pattern Recognition, 1999, 32(6): 947-971.

[11]SHIH F Y, CHUANG C F, GADDIPATI V. A modified regulated morphological corner detector[J]. Pattern Recognition Letters, 2005, 26(7): 931 - 937.

编 辑 漆 蓉

New Algorithm for Corner Detection with Regulated Morphology

ZHAO Qin-jun1and ZHAO Dong-biao2

(1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics Nanjing 210016;2. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics Nanjing 210016)

A novel corner detection algorithm based on regulated morphology is proposed in this paper.Symmetric disk structure element is adopted in the algorithm. Firstly, by choosing a proper regulated parameter, the image is processed with a series of operations such as regulated erosion and regulated dilation to get accurate positions of the convex and concave corners respectively, and then all corners in the image are obtained by combing the two kinds of corners together. The use of disk structure element highly decreases the computation cost.The method based on regulated morphology is more precise than methods based on traditional morphology. The experiment results prove that when a proper value of the regulated parameter is chosen, the proposed new detector can precisely detect corners in images.

corner detection; dilation; erosion; mathematical morphology; structure element

TP391

A

10.3969/j.issn.1001-0548.2010.06.017

2009- 04- 27;

2009- 10- 28

江苏省自然科学基金(BK2003005)

赵钦君(1981- )，男，博士生，主要从事机器视觉、图像处理与模式识别方面的研究.