综合的结构可靠度函数预测模型

汪忠来 ，黄洪钟，王贵宝

(电子科技大学机械电子工程学院 成都 610054)

综合的结构可靠度函数预测模型

汪忠来 ，黄洪钟，王贵宝

(电子科技大学机械电子工程学院 成都 610054)

基于结构产品的现场失效数据样本较少以及物理结构模型可靠性评估存在误差，建立了综合考虑失效数据和结构失效模式及衰退机理的结构可靠度函数预测模型。采用一阶可靠性方法(FORM)进行物理结构可靠度评估，将失效数据方法得到的可靠度和物理结构方法得到的可靠度作为输入进行模糊回归，估计概率分布参数。建立的可靠度函数预测模型能较精确地预测结构产品随时间变化的可靠度，为结构产品的可靠性设计以及维修策略的制定奠定了理论基础。通过实例验证了该模型的可行性。

衰退机理; 失效数据; 失效模式; 可靠度预测; 结构可靠度

可靠度预测作为可靠性工程的重要组成部分，是可靠性优化设计和维修策略制定的前提。目前，对于结构产品主要有两种可靠度预测方法：(1)根据失效数据进行统计分析[1-2]；(2)根据产品的失效模式和衰退机理对结构在物理层面进行可靠度预测[3-4]。在实际工程中，对很多产品来说，获取大量的失效数据是困难的，甚至是不可能的。由于样本少，统计分析方法预测精度比较低。而物理层面可靠度预测方法基于产品的失效模式和衰退机理，直接与产品的物理结构相关。通过对物理结构进行建模，利用广义应力强度干涉模型进行可靠度函数预测。该方法扩展了基于失效模式的静态可靠度预测[5-7]，但其预测的结果具有误差，如建模误差、计算近似误差[8]。由于随机设计变量和随机参数的分布特性很难确定，物理方法用某种特定的概率分布近似随机设计变量和随机参数的分布特性，从而忽略了主观不确定性。非概率可靠度预测方法充分考虑了主观不确定性，并得到了广泛的关注[9-11]，但是通过非概率方法预测到的可靠度是一个区间，不利于可靠性设计和维修策略的制定。

到目前为止，人们习惯将统计可靠度预测方法和物理可靠度预测方法划分为两个不同的领域。实质上，两者是密切联系的，不同之处在于两者是从不同的角度预测结构产品的可靠度。本文综合考虑统计方法和物理方法得到的可靠度进行结构产品的可靠度函数预测，以提高预测精度。由于主观因素(如失效数据的模糊性和用某种特定的分布近似随机变量的分布特性)对两种方法的可靠度计算的影响，将得到的可靠度作为模糊数处理，并利用模糊回归对可靠度函数的参数进行评估。

1 基于物理模型的可靠度预测方法

对于大多数产品，产品性能会随着时间衰退。因此，可以通过时间相关的广义应力强度干涉模型计算产品的可靠度函数，即：

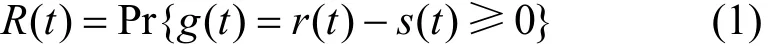
式中 R(t)为产品的可靠度函数；r(t)为产品的性能(广义强度)，为随机过程；s(t)为导致产品失效的外部因素(广义应力)，为随机过程；g(t)为产品的极限状态函数。

可靠度的预测是建立在产品物理结构的基础上的。产品的广义强度r(t)和广义应力s(t)是确定性设计变量d(t)、随机设计变量X(t)和随机参数P(t)的函数。X(t)和P(t)的区别在于前者在设计过程中是可以控制的，而后者则不能。因此，产品的极限状态函数可以表示为 g ( d ( t), X ( t), P ( t),t)。产品可靠度随时间变化曲线如图1所示。式中 b =R(ti)为三角模糊数中心；l1为支撑集宽度，由随机设计变量及随机参数服从假定分布的程度决定。如果随机设计变量及随机参数服从假定分布的程度比较小，则l1选大一些。

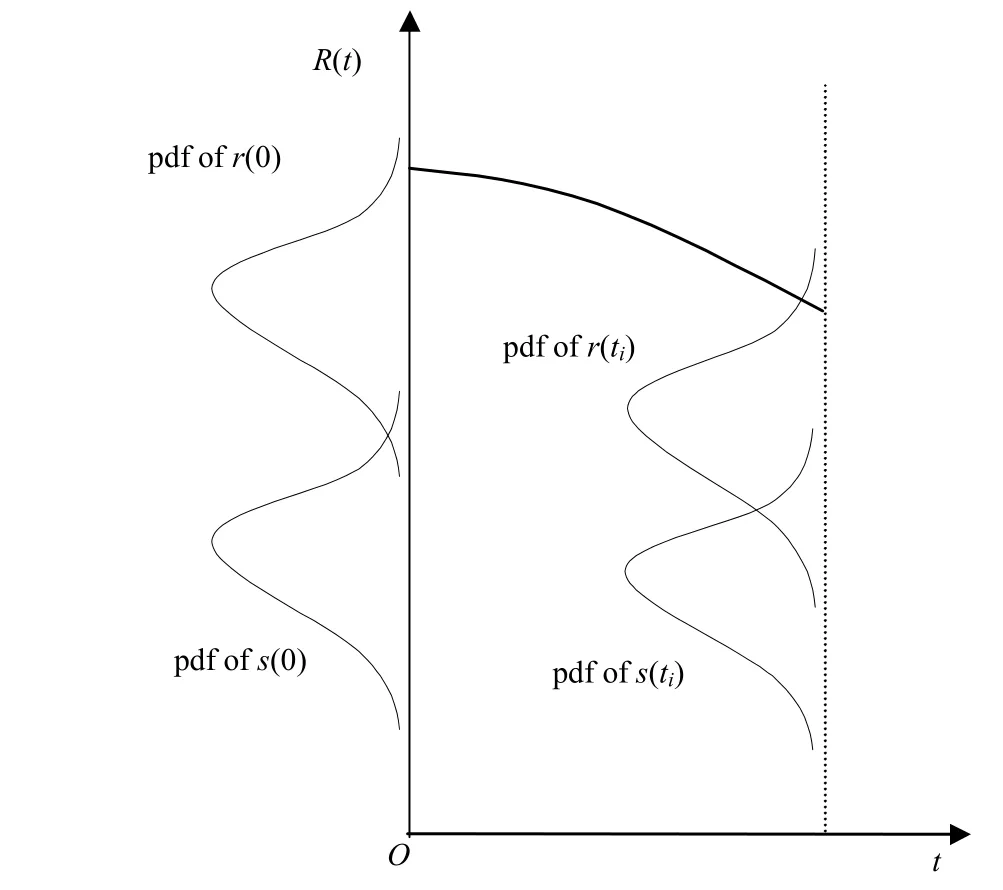
图1 产品可靠度随时间变化规律

2 统计分析可靠度预测

在实际的工程中，失效数据的获取往往是通过在特定时间段内产品的失效个数实现，并转化为产品可靠度：

3 建立可靠度函数预测模型

由于很难获取很多的失效数据，只能得到少数几个时刻点的可靠度。通过物理模型可靠度预测方法，各个时刻ti的可靠度 R (ti)均可以获取。但是，如果过多地选择物理模型方法得到的样本，则统计方法得到的可靠度在可靠度函数预测中的作用会比较小。因此，本文给出几种样本选择的参考标准：

(1)如果失效数据特别少，则多选几个物理模型得到的样本，从而减少由于样本太少产生的误差；

(2)如果建立的物理模型的误差较小，则多选几个物理模型得到的样本，提高它们在可靠度函数预测中的比重；

(3)在失效数据不是特别少又不能确定物理模型的误差不是较小的情况下，少选几个物理模型得到的可靠度，失效数据被认为更可信。

将两种方法得到的可靠度信息完全按照时间先后顺序排列，允许有相同时刻点的可靠度信息，并将两种方法得到的可靠度R(t)和R′(t)用 R (ti)表示，如表1所示。

表1 时间对应的可靠度信息

指数分布在可靠性工程领域是最基本的、最常用的分布。若用指数分布描述产品的寿命分布，则可靠度函数为：

4 算例分析

本文对一种压力容器的可靠度函数进行预测，其结构如图2所示。

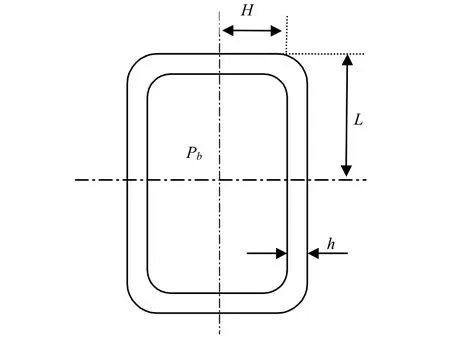
图2 压力容器结构图

图中，H、L、h是随机设计变量，bP是随机参数。当应力大于屈服强度时，产品被认为失效，则极限状态函数为：

式中 h0为初始壁厚。随机设计变量和随机参数的分布如表2所示。用FORM计算时刻为5个月、15个月、25个月、35个月和45个月时的可靠度，如表3所示，并取l1= 0 .000 5。根据某厂家收集的信息，通过失效数据统计分析得到的可靠度如表4所示，并取l2= 0 .000 8。

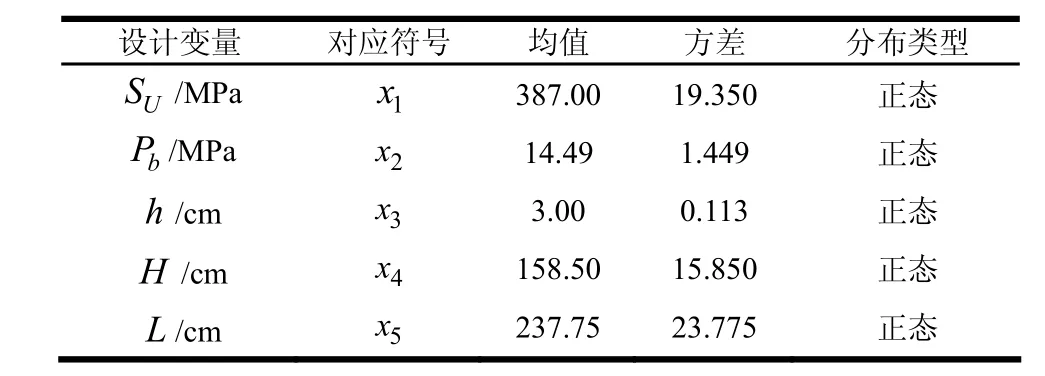
表2 随机变量的分布

表3 物理模型方法可靠度

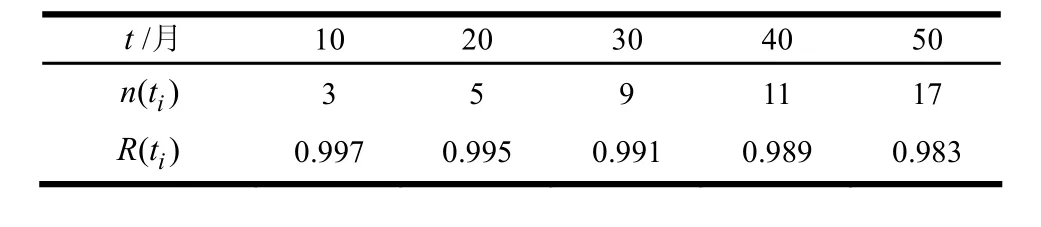
表4 失效数据统计的可靠度(1 000样本)

取 H = 0 .95，通过优化式(11)计算得到模糊系数为(0.000 3,0.009 4)。则拟合表达式为：

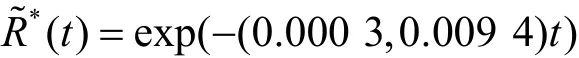
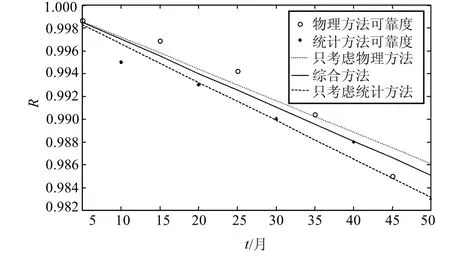
图3 不同方法预测的可靠度函数曲线

由于在时间区间[0, 50]，可靠度降低比较慢，指数分布函数接近于直线。如果只使用统计方法，则会由于样本较少产生较大的误差，如图3中短线段曲线所示。如果只采用物理方法，则会由于建模、计算近似等产生偏向性误差，如图3中点划线所示。综合的可靠度函数预测方法可以从两个角度理解：(1)由于现场数据信息的加入部分纠正了物理方法产生的偏向性误差；(2)物理方法为统计方法增加了样本，减少了由于样本数量较少带来的统计误差。

5 结 论

在可靠性工程领域，通常使用失效数据的统计分析预测结构产品(如机械零件)的可靠度分布函数，但很难获取大量的失效数据。因此，该方法预测可靠度函数与实际存在一定的偏差，并且还会由于样本量太少而无法进行。

通常，在产品设计领域使用基于物理结构和衰退机理的可靠度函数预测方法，而没能发挥其在可靠性工程领域中的应用。实质上，统计分析和基于物理结构的可靠度函数预测方法是从两个不同的角度预测结构产品的可靠度函数，两者针对同一个对象，具有密不可分的联系。

本文充分考虑了基于物理结构方法的误差、主观不确定性和统计方法的主观不确定性，建立了一种综合的可靠度函数预测模型。该模型提高了可靠度函数的预测精度，并为更精确的可靠性设计和维修策略的制定奠定了基础。

[1]ANDREWS J D, MOSS T R. Reliability and risk Assessment[M]. New York: ASME Press, 2002.

[2]陈光宇, 黄锡滋, 唐小我. 故障树模块化分析系统可靠性[J]. 电子科技大学学报, 2006, 35(6): 989-992.

CHEN Guang-yu, HUANG Xi-zi, TANG Xiao-wo. Modular solutions for fault tree analysis of reliability of systems[J].Journal of University of Electronic Science and Technology of China, 2006, 35(6): 989-992.

[3]STEWART M G. Time-dependent reliability of existing RC structure[J]. Journal of Structural Engineering, 1997, 123(7):896-902.

[4]WANG Z L, DU X, HUANG H Z. Reliability-based lifecycle optimization with maintenance consideration[C]//Proc of 14th ISSAT Conference on Reliability and Quality in Design. Orlando: [s.n.], 2008.

[5]DU X, CHEN W. Sequential optimization and reliability assessment method for efficient probabilistic design[J].ASME Journal of Mechanical Design, 2004, 126(2):225-233.

[6]DU X. Unified uncertainty analysis by the first order reliability method[J]. ASME Journal of Mechanical Design,2008, 130(2): 09140101-09140110.

[7]BOWLING A P, RENAUD J E, NEWKIRK J T, et al.Reliability-based design optimization of robotic system dynamic performance[J]. ASME Journal of Mechanical Design, 2007, 129(1): 449-454.

[8]MAHADEVAN S, REBBA R. Inclusion of model errors in reliability-based optimization[J]. ASME Journal of Mechanical Design, 2006, 128(4): 936-944.

[9]MOURELATOS Z P, ZHOU J. A design optimization method using evidence theory[J]. ASME Journal of Mechanical Design, 2006, 128(4): 901-908.

[10]DU L, CHOI K K, YOUN B D, et al. Possibility-based design optimization method for design problems with both statistical and fuzzy input data[J]. ASME Journal of Mechanical Design, 2006, 128(4): 928-935.

[11]郭书祥, 张 陵, 李 颖. 结构非概率可靠性指标的求解方法[J]. 计算力学学报, 2005, 22(2): 227-231.

GUO Shu-xiang, ZHANG Ling, LI Ying. Procedure for computing the non-probabilistic reliability index of uncertain structures[J]. Chinese Journal of Computation Mechanics, 2005, 22(2): 227-231.

[12]LAUMAKIS P J, HARLOW G. Structural reliability and monte carlo simulation[J]. International Journal of Mathematical Education in Science and Technology, 2002,33: 377-387.

[13]HASOFER A M, LIND N C. Exact and invariant second-moment code format[J]. ASCE Journal of the Engineering Mechanics Division, 1974, 100(EM1):111-121.

[14]HOHENBICHLER M, GOLLWITZER S, KRUSE W, et al.New light on first- and second-order reliability methods[J].Structural Safety, 1987, 4: 267-284.

[15]SOMMER A M, NOWAK A S, THOFT-CHRISTENSEN P.Probability-based bridge inspection strategy[J]. Journal of Structural Engineering, 1993, 119: 3520-3536.

编 辑 黄 莘

Integrated Prediction Model for Structural Reliability Function

WANG Zhong-lai, HUANG Hong-zhong, and WANG Gui-bao

(School of Mechatronics Engineering, University of Electronic Science and Technology of China Chengdu 610054)

Since the samples for some structural products are very few and the reliability obtained from the physical model has some errors, an integrated reliability function prediction model based on failure data, failure modes and degradation mechanics of the structural product is proposed. First order reliability method (FORM)is implemented to calculate the reliability based on physical model. Both the reliability from failure data and physical model are considered as fuzzy inputs to estimate the parameters in the probability distribution. The proposed reliability function prediction model can accurately predict the time-dependent reliability of the structural product.Reliability-based design and maintenance strategy can be properly made in terms of the predicted time-dependent reliability. An engineering example is used to illustrate the proposed reliability function prediction model.

degradation mechanics; failure data; failure mode; reliability prediction; structural reliability

TJ81+0.321

A

10.3969/j.issn.1001-0548.2010.06.031

2009- 04- 25；

2009- 12- 17

国家自然科学基金(50775026)；教育部高等博士学科点专项科研基金(20060614016)

汪忠来(1980- )，男，博士生，主要从事可靠性预测及基于可靠性、稳健设计等方面的研究.