星敏感器模型参数分析及校准方法研究

王洪涛，罗长洲，王 渝，赵述芳

(1. 北京理工大学自动化学院 北京 海淀区 100081; 2. 北京控制与电子技术研究所 北京 海淀区 100038)

星敏感器模型参数分析及校准方法研究

王洪涛1，罗长洲2，王 渝1，赵述芳1

(1. 北京理工大学自动化学院 北京 海淀区 100081; 2. 北京控制与电子技术研究所 北京 海淀区 100038)

对星敏感器的实际测量模型和模型参数的校准方法进行了深入研究。首先，在星敏感器理想测量模型的基础上，充分考虑焦距偏差、光学系统的成像畸变、图像传感器感光面的倾斜、图像传感器感光面的旋转和主点偏差等因素对导航星实际成像位置的影响，用几何的方法建立了星敏感器的实际测量模型，其次，分析了各因素对星敏感器测角精度的影响规律；通过实测校准数据，借助最小二乘法求解模型参数，完成了星敏感器的校准。实验结果表明，测角精度得到了提高。

校准; 最小二乘; 模型; 星敏感器

星敏感器是一种高精度的姿态敏感器，在投入使用前，其焦距、主点、光学系统的成像畸变等参数必须经过精确的测量，称为星敏感器的校准，是星敏感器研究和应用中的一项关键技术。目前，星敏感器的校准方法有多种[1-6]，普遍存在的一个问题是建模时考虑的误差因素不够全面。本文充分考虑了影响星敏感器测量模型的各种因素，用几何的方法建立了星敏感器的精确测量模型，并通过实测校准数据，利用最小二乘法求解模型参数，从而完成星敏感器的校准。

1 星敏感器的测量模型

1.1 星敏感器的理想测量模型

文献[6]提出了星敏感器的测量模型，如图1所示。星光矢量OsPi与星敏感器光轴的夹角θ的正切为：

θ角的测量精度是星敏感器整体精度的基础[6-7]。θ角可分解成两个角度θx和θy，其中θx表示星光矢量OsPi在面ZsOsXs上的投影 OsPxi与星敏感器光轴的夹角，θy表示导航星矢量OsPi在面ZsOsYs上的投影OsPyi与星敏感器光轴的夹角，相应的正切值分别为：

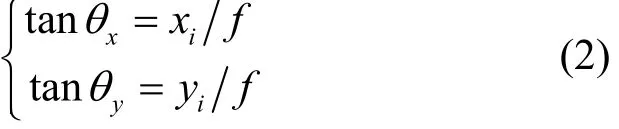
1.2 星敏感器的实际测量模型

由于实际光学系统的“离焦成像”和装配误差共同引起的焦距偏差、光学系统的成像畸变、图像传感器感光面的倾斜、图像传感器感光面的旋转和主点偏差等因素的影响，实测星点质心P′i(x′i,y′i)与理想星点质心Pi(xi,yi)并不重合，从而引入测角误差Δθ：

图2 从理想测量模型到实际测量模型的5个步骤

从理想星点质心Pi到实测星点质心iP′的具体变换过程可分为焦距偏差、光学系统的成像畸变、感光面的倾斜、感光面的旋转和主点偏差5个步骤，如图2所示。

1.2.1 焦距偏差对星点质心位置的影响

为了达到亚像元的定位精度，实际光学系统采取“轻微离焦”的成像方式。另外，由于装配误差的影响，实际图像传感器的感光面也并不能精确安装在光学系统的焦点处。因此，理想星点的质心Pi实际成像在图3所示平面Ⅱ中的 Pfi，若Pi和 Pfi在星敏感器坐标系OsXsYsZs中的坐标分别为(xi,yi,zi)和( xfi, yfi,zfi)，则：

式中 f 为焦距的理想值；Δf 为焦距偏差。

图3 焦距偏差与星点质心位置

1.2.2 成像畸变对星点质心位置的影响

在设计星敏感器光学系统时，既要考虑校正几何畸变，又要考虑校正色差。但如果要使两种校正都很理想，设计出来的光学系统往往非常复杂，不但加大了设计难度，也对制造工艺带来一定的困难，提高了光学系统的制造成本。在几何畸变和色差校正不可兼得的情况下，首先要确保色差校正[8]，因而大多数光学系统都存在不同程度的几何畸变。几何畸变主要包括径向畸变和切向畸变[9-10]。研究表明，切向畸变比较小，可忽略不计[11]。因此，由于实际光学系统径向畸变的影响， Pfi实际位于平面Ⅱ内的Pfgi，如图4所示若Pfgi在星敏感器坐标系OsXsYsZs中的坐标为(xfgi,yfgi,zfgi)，则：

式中 g1为一阶径向畸变系数。

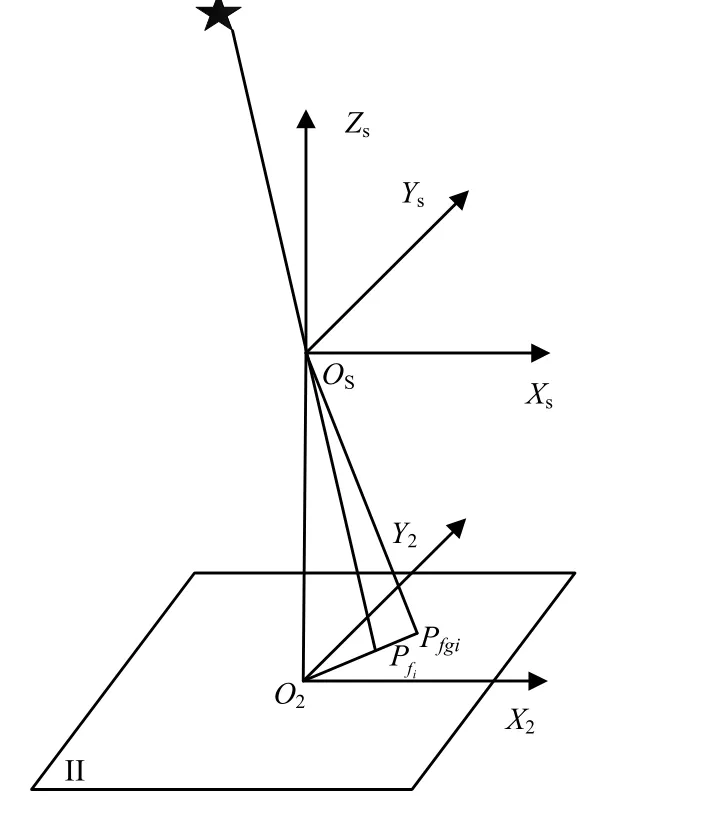
图4 成像畸变与星点质心位置

1.2.3 感光面的倾斜对星点质心位置的影响

实际图像传感器感光面并不严格垂直于光学系统的光轴。可假设平面Ⅱ绕X2轴正向旋转φx角得到平面Ⅲ，Pfgi与平面Ⅲ 的交点为Pfgφxi，如图5所示，然后平面Ⅲ 绕Y3轴正向旋转φy角得到平面Ⅳ，实际图像传感器即安装在该平面上，OsPfgφxi与平面Ⅳ的交点为Pfgφi，此点即为实测星点质心iP′，如图6所示。若Pfgφi在星敏感器坐标系OsXsYsZs中的坐标为(xfgφi,yfgφi,zfgφi)，则：

图5 感光面倾斜φx角与星点质心位置

图6 感光面倾斜φy角与星点质心位置

1.2.4 感光面的旋转对星点质心位置的影响

图7中的虚线框是理想情况下图像传感器感光面的安装方式，然而实际安装时会与理想安装方式有一个旋转角β，相当于坐标系O2X3Y3绕星敏感器坐标系OsXsYsZs的Zs轴正向旋转β角得到坐标系O4X4Y4。此时，若Pfgφi在坐标系O4X4Y4中的坐标为(xfgφβi,yfgφβi)，则：

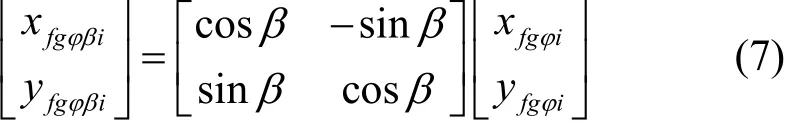
图7 感光面旋转β角与星点质心位置

1.2.5 主点偏差对星点质心位置的影响

实际上，不能精确定位主点O2(图像传感器感光面与光轴的交点)在图像传感器感光面的位置，只能规定一个位置。如图8所示OP点，若OP在坐标系O4X4Y4中的坐标为(Δx,Δy)，实测星点质心iP′在星敏感器坐标系OsXsYsZs中的实测坐标为(x′pi,y′pi,z′pi)，则：

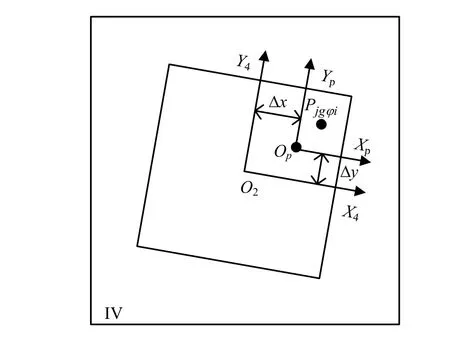
图8 主点偏差与星点质心位置

2 模型参数分析

由以上的分析可知，焦距偏差、光学系统的成像畸变、图像传感器感光面的倾斜、图像传感器感光面的旋转和主点的偏移都会使星点质心的实际位置偏离理想位置，从而引入测角误差。各模型参数对θx和θy测角精度的影响如图9所示。

(1)对于同一星点质心位置，焦距偏差越大，测角误差越大；对于同一焦距偏差，星点质心位置离主点越远，测角误差越大。

(2)对于同一星点质心位置，径向畸变系数越大，测角误差越大；对于同一径向畸变系数，星点质心位置离主点越远，测角误差越大。

(3)对于同一星点质心位置，感光面倾斜角越大，测角误差越大；对于同一感光面倾斜角，星点质心位置离主点越远，测角误差越小。

(4)对于同一星点质心位置，感光面旋转角越大，测角误差越大；对于同一感光面旋转角，星点质心位置离主点越远，测角误差越大。

(5)对于同一星点质心位置，主点偏差越大，测角误差越大；对于同一主点偏差，星点质心位置离主点越远，测角误差越小。

图9 模型参数对测角精度的影响规律

实际星敏感器光学系统的一阶径向畸变小于0.02%，若感光面的倾斜角φx= φy= 0.1°，旋转角β = 0.1°，主点偏差为10 pixel，光学系统的一阶径向畸变、感光面的旋转角和主点偏差对测角精度的影响较大，焦距偏差和感光面的旋转角对测角精度的影响较小。

3 参数校准方法

3.1 校准数据获取

利用星敏感器原理样机、单星模拟器和二维精密转台即可完成校准数据采集。星敏感器固定，星模拟器安装在二维精密转台上。首先调整转台使星模拟器发出的星光和星敏感器感光面处于自准直状态，记录此时星点质心在像面像元坐标系中的坐标和转台的方位角A0、高低角E0，该质心坐标即为主点坐标 ( xF0,yF0)。以(A0,E0)为参考中心调整转台，使之在3°×3°范围内分别沿图像传感器感光面的两个坐标轴方向转动，每隔0.4°为一个测量位置，最后在感光面上形成密度均匀、分布均匀的星像点点阵，则：

3.2 最小二乘参数校准算法

式中 N为实验中测量的星像点个数。利用最小二乘法，即可求解出参数Δf、g1、φx、φy、β、Δx0和Δy0。将解出的参数代入式(9)和式(10)便可求得星点质心的理想值(xi,yi)，从而完成星敏感器的校准。

3.3 校准精度的评价

将解出的参数Δf、g1、φx、φy、β、Δx0、Δy0代入式(9)和式(10)求取星点质心的理想值(xi,yi)，利用式(14)再求测角误差，利用式(15)和式(16)分别求测角误差的均值和标准差，最用利用式(17)即可算出校准后星敏感器在x方向和y方向的测角精度：

4 校准实验及结果分析

表1 实验所用星敏感器的基本参数

图10 校准前和校准后x方向测角误差

图11 校准前和校准后y方向测角误差

5 结 束 语

本文充分考虑了影响星敏感器测量模型的各种因素，利用几何方法建立星敏感器的精确测量模型，分析了各种因素对星敏感器测角精度的影响规律，并通过实测校准数据，借助最小二乘法求解模型参数，完成了星敏感器的校准。实验结果表明，未校准前，x和y方向的测角精度分别为19.6″和17.8″；校准后，测角精度可分别达到1.6″和2.3″，进一步验证了所建立的星敏感器测量模型的正确性。

[1]FEI Xing, YING Dong, ZHENG You. Laboratory calibration of star tracker with brightness independent star identification Strategy[J]. Optical Engineering, 2006, 45(6): 063604.

[2]刑 飞, 董 瑛, 武延鹏, 等. 星敏感器参数分析与自主校正[J]. 清华大学学报(自然科学版), 2005, 45(11):1484-1488.

XING Fei, DONG Ying, WU Yan-peng, et al. Star tracker parametric analysis for autonomous calibration [J]. Journal of Tsinghua University Science and Technology, 2005,45(11): 1484-1488.

[3]张 辉, 田 宏, 袁家虎, 等. 星敏感器参数标定与误差补偿[J]. 光电工程, 2005, 32(9): 1-4.

ZHANG Hui, TIAN Hong, YUAN Jia-hu, et al. Parameter calibration and error compensation of star sensor[J].Opto-Electronic Engineering, 2005, 32(9): 1-4.

[4]郝雪涛, 张广军, 江 洁. 星敏感器模型参数分析与校准方法研究[J]. 光电工程, 2005, 32(3): 5-8.

HAO Xue-tao, ZHANG Guang-jun, JIANG Jie. Star sensor model parameter analysis and calibration method[J].Opto-Electronic Engineering, 2005, 32(3): 5-8.

[5]魏新国, 张广军, 樊巧云, 等. 基于RAC约束的星敏感器在轨校准方法[J]. 光学精密工程, 2008, 16(10): 2009-2013.

WEI Xin-guo, ZHANG Guang-jun, FAN Qiao-yun, et al.On-orbit calibration of star sensor based on radial alignment constraint[J]. Optics and Precision Engineering, 2008,16(10): 2009-2013.

[6]LIEBE C C. Accuracy performance of star trackers-atutorial[J]. IEEE Transactions on Aerospace and Electronic Systems,2002, 38(2): 587-589.

[7]JU G H. Autonomous star sensing, pattern identification,and attitude determination for spacecraft: an analytical and experimental study[D]. Texas: Texas A&M Univesity, 2001.

[8]刘堂友, 董爱华. 精确校正图像的径向畸变和倾斜失真[J]. 中国图象图形学报, 2007, 12(10): 1935-1938.

LIU Tang-you, DONG Ai-hua. Precisely correct radial and oblique distortion of camera image[J]. Journal of Image and Graphics, 2007, 12(10): 1935-1938.

[9]DEVERNAY F, FAUGERAS O. Straight lines have to be straight: automatic calibration and removal of distortion from scenes of structured environments[J]. Machine Vision and Applications, 2001, 13(1): 14-24.

[10]SWAMINATHAN R, NAYAR S K. Non-metric calibration of wide-angle lenses and polycameras[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2000, 22(10): 1172-1178.

[11]TSAI R Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal of Robotics and Automation, 1987, 3(4): 323-344.

编 辑 税 红

Star Sensor Model Parametric Analysis and Calibration Method Study

WANG Hong-tao1, LUO Chang-zhou2, WANG Yu1, and ZHAO Shu-fang1

(1. School of Automation, Beijing Institute of Technology Haidian Beijing 100081 2. Beijing Institute of Control and Electronic Technology Haidian Beijing 100038)

An actual measurement model of star sensor is established by geometrical method. The effect of relative factors to the actual imaging location of navigation star is considered into the ideal measurement model of star sensor. These factors include focal length deviation, optical lens distortion, image sensor tilt, image sensor rotate, primary point bias, etc. The affecting law of the factors on angle-measuring accuracy of star sensor is analyzed. The star sensor is calibrated through the measured calibration data and the model parameters solved by least square method. The experimental results show that the angle measurement accuracy of x and y directions is 1.6″ and 2.3″ after calibration, but 19.6″ and 17.8″ before calibration.

calibration; least-squares; model; star sensor

V488.22

A

10.3969/j.issn.1001-0548.2010.06.016

2009- 03- 01;

2009- 06- 03

王洪涛(1981- )，男，博士生，主要从事星敏感器及相关技术方面的研究.