利用LC滤波器实现延迟混沌及控制的电路实验
2010-02-01陈菊芳田小建单江东
陈菊芳,田小建,单江东
(1.吉林大学电子科学与工程学院,吉林长春130012;2.东北师范大学物理学院,吉林长春130024)
1 引 言
近年来,随着混沌现象及理论被引入到大学物理教学中,有的院校增设了非线性电路实验课[1-5].延迟混沌系统因其具有无穷维数且能产生混沌和超混沌信号而受到广泛关注.有关延迟混沌系统的理论分析和数值计算方面的研究较多[6-9],但实验方面的报道很少.由于混沌信号具有伪随机噪声的特性,如何对混沌信号进行有效延迟是设计延迟混沌电路的难点和关键.
本文采用基本的电子元器件来实现延迟混沌电路.利用L C低通滤波器在通带内具有良好群时延特性来实现对混沌信号的有效延时,并在Logistic延迟混沌系统中加以实现,同时利用简单的二极管限幅电路实现混沌控制.该延迟混沌及控制电路使用的元件方便易得,成本低,演示现象丰富,宜于引入实验教学中.
2 混沌电路设计
典型的Logistic延迟方程为[10]
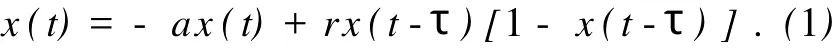
当a=2.6,r=10.4,τ=5时,该系统是混沌的.
实现系统(1)的电路见图1.设延时时间为τd,运放A1构成积分器,其输出电压为u(t),A3构成反向加法器,A2构成同相放大器,放大由延时电路输出的延时信号,以保证A2的输出电压满足u2(t)=u(t-τd)的要求.
电路的状态方程为作如下标量变换:
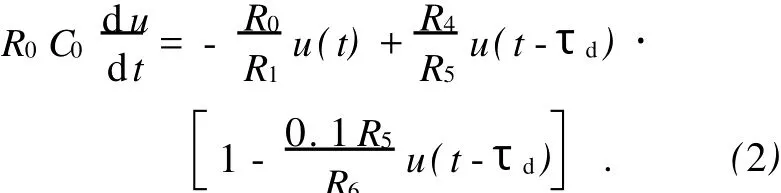
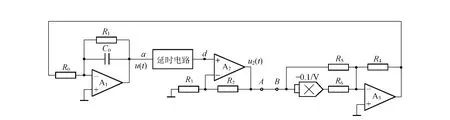
图1 Logistic延迟混沌电路
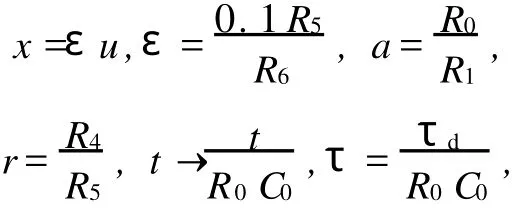
则方程(2)变为方程(1).
延时电路如图2所示.由普通的电感和电容构成,取标称的电感和电容,L=4.7 mH,2C=0.1μF,Ri=30Ω,Ro=300Ω,电感的直流损耗电阻RL=19.8Ω.为减少电路的损耗,采用电感元件相对较少的π型滤波器,取级数N=28.由于这种滤波器在通带内具有良好的群时延特性,且在通带内幅频特性平坦,只要混沌信号的频谱在滤波器的通频带内,即可实现良好的延时效果.由实验测得其截止频率fc=6.12 kHz,通带内传递函数值为|H(ω)|=-9.548 dB,延时时间τd=0.63 ms.通过对系统(1)的动力学特性分析可知,混沌信号的频谱基本在滤波器的截止频率内.
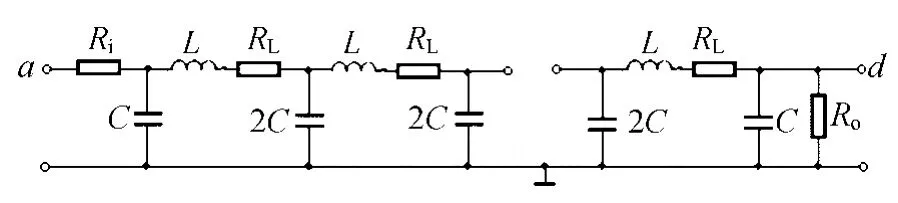
图2 延时电路
为满足系统(1)对各参量的要求,现选取R0=12.6 kΩ,C0=0.01μF,R1=4.85 kΩ,R2=2.13 kΩ,R3=1 kΩ,R4=10 kΩ,R5=0.96 kΩ,R6=0.48 kΩ.由示波器观测到的实验结果如图3所示.其中图3(a)为u(t)与u2(t)的时域图,u2(t)与u(t)的波形形状和大小基本相同,只是向后延迟了0.63 ms,即满足u2(t)=u(t-τd).图3(b)为u(t)与u(t-τd)的相图,显然是混沌吸引子,表明所设计的延时电路对混沌信号取得了很好的延时效果.
实验中,改变电阻R0,电容C0或延时电路中的电感和电容,都可以改变系统(1)中的延时时间τ,本文采用改变电阻R0来获得倍周期信号输出.图4(a)~(c)所示的是当R0取值分别为80 kΩ,57 kΩ,50.5 kΩ(同时R1应调整以保证a=2.6),即相当于系统(1)中的τ分别为0.79,1.10,1.25时,由电路观测到的1周期(1P)、3周期(3P)、6周期(6P)相图.

图3 电路的混沌时域波形和吸引子的实验结果
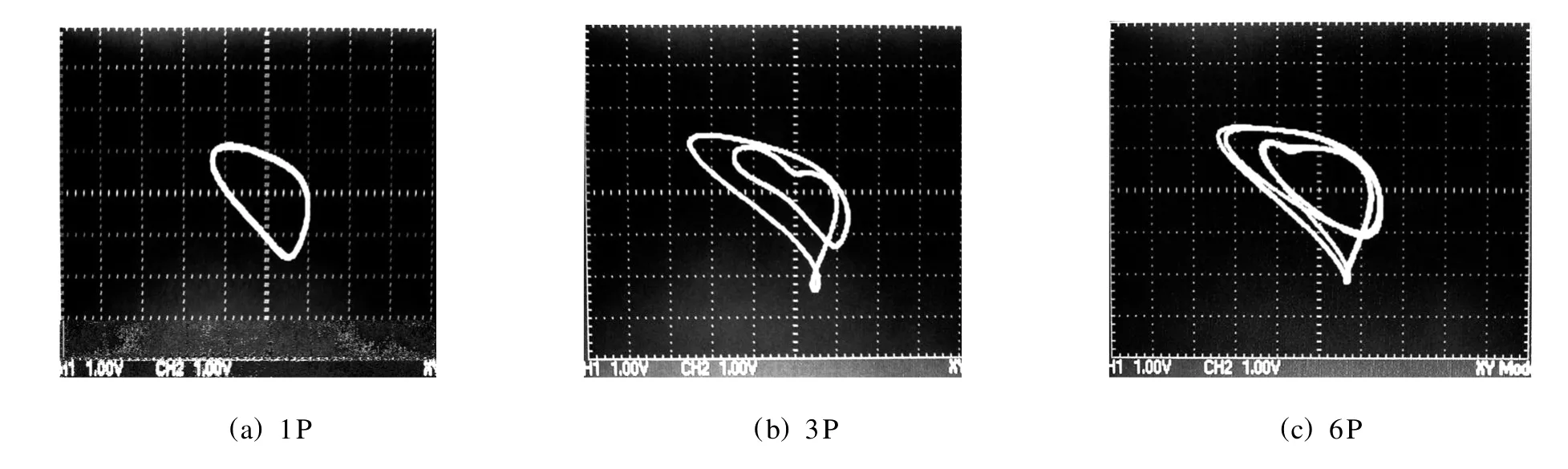
图4 电路的倍周期分岔的实验结果
3 实现控制的电路
利用二极管的单向导电性来对延时信号进行限幅,最终实现稳定住失稳周期轨道的目的.控制量的具体表达式为
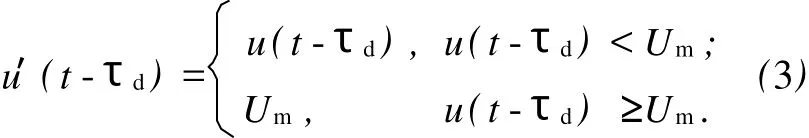
将u′(t-τd)代替方程(2)的u(t-τd),即可实现混沌的控制.
实现控制的电路如图5所示,将图1电路中的A和B两点断开,分别与图5电路中的对应点相连接,即可构成控制电路.显然,Um=UD+U0为阈值电压,UD=0.6 V为二极管的正向导通电压,通过调节电源电压U0可改变Um的大小,即可观测到电路的运动状态随Um的改变出现的各种变化,电阻R7=2 kΩ.
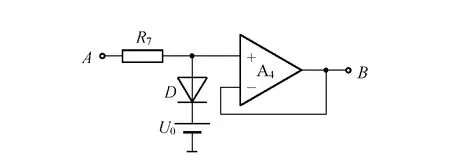
图5 控制电路
图6所示为当U0=3.47,3.54,3.59 V,即相当Um=4.07,4.14,4.19 V时被控电路的u(tτd)与u(t)的相图,电路分别呈现出1周期(1P)、4周期(4P)、8周期(8P)态,继续增大U0值,还观测到了6周期甚至更高周期的实验结果.
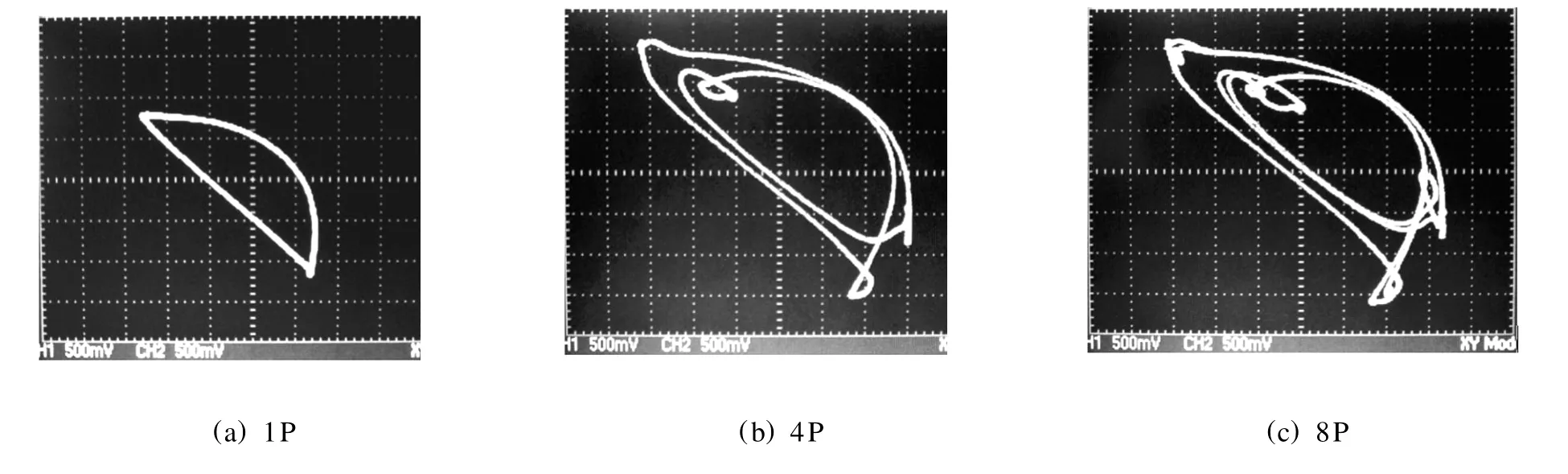
图6 电路被控制到周期的实验结果
4 结束语
以一阶Logistic延迟系统为例介绍了延迟混沌电路的设计方法,将L C低通滤波器用于混沌电路中来实现对混沌信号的延迟,克服了电路中延时电路难以实现的缺点,同时利用二极管的限幅作用来实现混沌控制,得到了多个稳定的周期轨道,说明限幅法不仅适用于控制一般的混沌系统,也适用于控制延迟混沌系统.该电路结构简单,实验现象丰富,便于在教学中演示及学生自行制作.
[1] 李蓉,原如领,汪华英,等.以科研带教学建设“非线性系统实验”课程[J].物理实验,2002,22(2):26-28.
[2] 孙萍,熊俊,曹惠贤,等.扭摆振动实验[J].物理实验,2006,26(12):3-7.
[3] 蒋达娅,王世红,肖井华.混沌专题系列研究型实验介绍[J].物理实验,2007,27(1):17-19.
[4] 刘恒,陈得海,夏彬,等.变形蔡氏电路中的混沌控制及Pspice仿真研究[J].物理实验,2007,27(3):35-38.
[5] 路峻岭,王延吉,王长江,等.滚球混沌运动演示实验[J].物理实验,2007,27(12):3-5.
[6] Kye Won-Ho,Choi Muhan,Rim Sunghwan,et al.Characteristics of a delayed system with time-dependent delay time[J].Phys.Rev.E,2004,69:055202.
[7] Li C G,Liao X F,Yu J B.Hopf bifurcation in a prototype delayed system[J].Chaos,Solitons and Fractals,2004,19:779-787.
[8] Car A U.On the chaotic behaviour of a prototype delayed dynamical system[J].Chaos,Solitons and Fractals,2003,16:187-194.
[9] Kim C M,Kye W H,Rim S,et al.Communication key using delay times in time-delayed chaos synchronization[J].Phys.Lett.A,2004,33:235-240.
[10] Jiang M H,Shen Y,Jian J G,et al.Stability,bifurcation and a new chaos in the logistic differential equation with delay[J].Phys.Lett.A,2006,350:221-227.
