37M n5钢热变形行为与流变应力模型研究

王 孟,洪慧平,王晓明

(北京科技大学材料科学与工程学院,北京,100083)

近年来,随着石油工业的快速发展,用于生产油井管的管坯钢用量不断增大,对其质量的要求也越来越高。37M n5管坯钢是生产J55级石油套管的专用钢种,其表面质量和内部组织的技术要求较严[1]。生产过程中,裂纹、折叠等缺陷是造成J55油井管不合格的主要原因[2]。目前,对37M n5钢质量缺陷的研究主要集中在钢水冶炼过程和连铸坯质量方面[1-4],而在高温变形过程中不合理的受力方式也是造成37M n5钢产品不合格的重要因素。为此,本文研究37M n5钢的热变形行为,为其合理的热加工工艺的制定和变形过程的数值模拟提供理论和实验依据。

1 实验材料与方法

热压缩试样取自37M n5热轧棒材,其化学成分如表1所示。将试样加工成φ10 mm×15 mm的圆柱体,在Gleeble-1500热模拟实验机上进行不同变形条件下的压缩实验。变形温度为800、900、1 000、1 150℃,变形速率为0.1、3、10 s-1。试样以10℃/s的升温速率加热到1 250℃,保温5 min,再以5℃/s的速率降温至设定的热变形温度,保温30 s以消除试样温度梯度,然后按预先设定的变形温度和应变速率进行压缩变形,最大真应变为0.8,变形结束后快速淬水冷却。

实验中采集的应力应变数据由文献[5]中所提供的方法判定其有效性。

表1 37Mn5钢的化学成分(w B/%)Table 1 Chem ical com positions of 37Mn5 steel

2 结果与分析

图1 37Mn5钢的应力应变曲线Fig.1 True stress-strain curve of 37Mn5 steelat strain rate of 0.1 s-1

2.1 应力-应变曲线

图1所示为37M n5钢在变形速率为0.1 s-1、变形温度为800～1 150℃的条件下热压缩时的应力应变曲线图。其中900～1 150℃条件下应力应变曲线的总体变化规律为流变应力首先随真应变的增加迅速上升,出现峰值后有所下降,达到一定真应变后,开始趋于平稳。表明37M n5钢在此条件下的变形属于动态再结晶型。变形温度越高,同一应变值对应的应力值越低,且峰值应力向应变量减小的方向移动。在800℃变形后的应力应变曲线中,流变应力随应变量的增加急剧上升,达到一定应变后由于动态回复的软化作用,上升趋势变得缓慢,但加工硬化仍占上风,较大应变时,曲线的最后阶段仍为上升,此时的变形属于动态回复型。

2.2 应变硬化率-流变应力曲线

图2为37M n5钢在变形速率为0.1 s-1时的应变硬化率θ与流变应力σ的关系曲线,应变硬化率θ是流变应力曲线上相应各点的斜率,即θ=dσ/dε。θ-σ曲线可更准确地确定流变应力曲线的特征值[6-7]。对各条真应力真应变曲线进行微分处理,得到相应的θ-σ曲线,曲线与直线θ=0交点处的应力即为各变形条件的峰值应力σp,对θσ曲线进行外推(如图2中虚线),外延线与θ=0交点的值即为饱和应力σss的值。

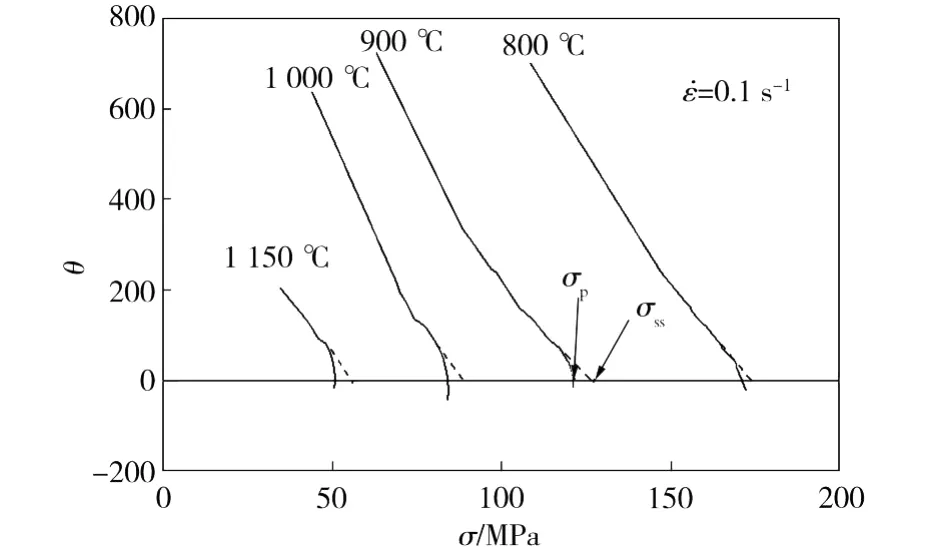
图2 37Mn5钢的θ-σ曲线Fig.2θ-σcurve of 37Mn5 steel

2.3 流变应力本构方程的建立

通过对不同热加工数据的研究,Sellars等[8]提出了一种包含变形激活能Q和温度T的本构方程,即

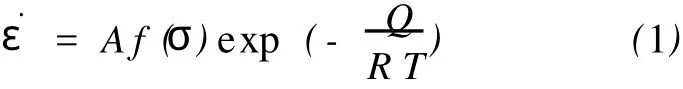
式(1)也称为A rrhenius方程。而应力函数f(σ)具有以下3种常见的形式[9]:

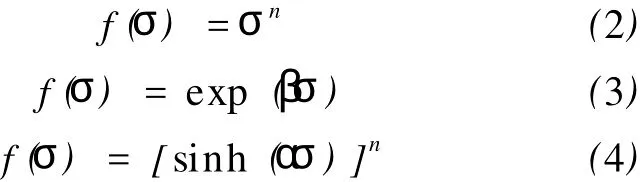
式中:α=β/n,M Pa-1;n为常数;β为常数,M Pa-1。

一般认为,式(2)适用于应力较低(ασ<0.8)的热变形;式(3)适用于应力较高(ασ>1.2)的热变形;式(4)适用于所有应力下的热变形,可在相应的应力范围内简化为式(2)、式(3)。文献[10]指出,不仅峰值流变应力σp和稳态流变应力σs,任意时刻的流变应力都符合式(4)。本文计算采用图2中确定的峰值应力σp。

材料在高温塑性变形时应变速率受热激活过程的控制,应变速率与温度之间的关系可用温度补偿的应变速率因子Zener-Hollomon参数(Z参数)表示:

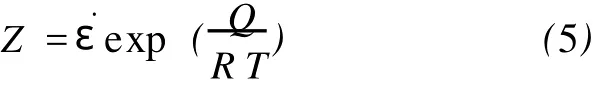
分别将式(2)、式(3)代入式(1)中可得:

温度恒定的情况下,分别对式(6)和式(7)两边取对数,可得的函数关系式,再将两式对求偏导数,则可得:·

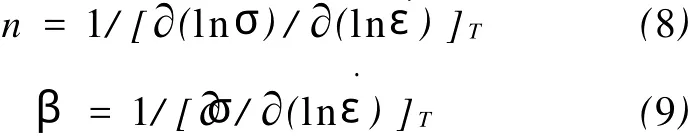
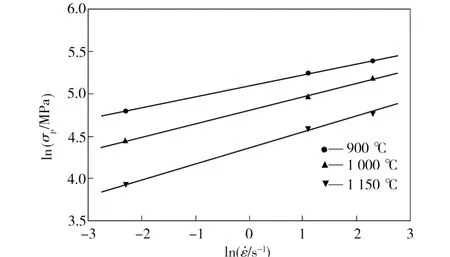
图3 lnσp与之间的关系Fig.3 Relationship between lnσp and

图4 σp与之间的关系Fig.4 Relationship betweenσp and

将式(4)代入式(1)可得:

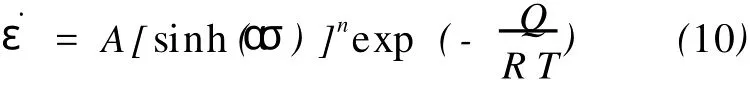
对式(10)两边取对数,得:

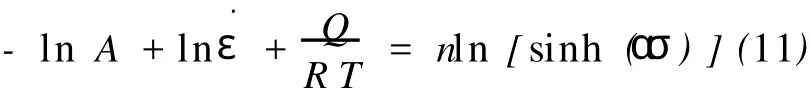
一定时,式(11)对1/T求偏导数得:

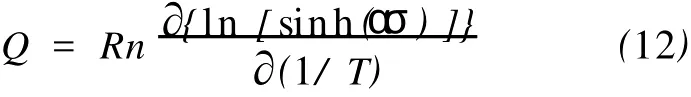
应用最小二乘法进行回归,得到ln[sinh(ασp)]与1/T的关系曲线,如图5所示。图5中,取直线的平均斜率代入式(12),可得变形激活能Q。再由式(11)代入数据计算即可求得常数A。

图5 ln[sinh(ασp)]与1/T之间的关系Fig.5 Relationship between ln[sinh(ασp)]and 1/T

依照以上方法,代入数据计算得到37M n5钢的热变形激活能Q以及其他材料常数(α、β、n和A)的值,结果如表2所示。

表2 式(10)中各参数的值Table 2 Parameters in Eq.(10)

将所得数据代入式(10),可得37M n5钢峰值流变应力本构方程如下:

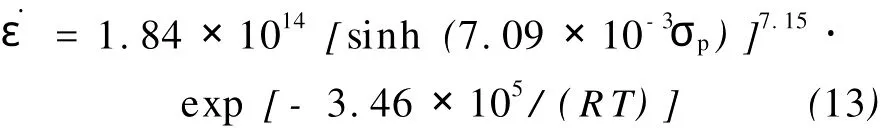
由双曲线正弦函数定义及式(5),可将式(13)改写为

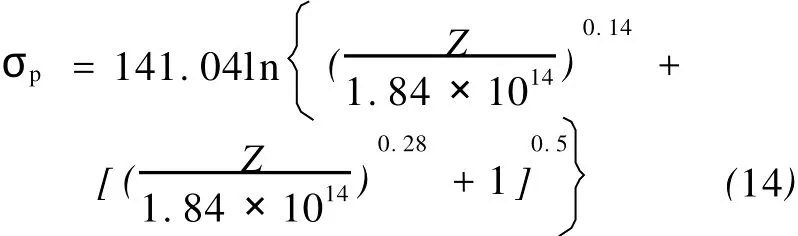
其中Z参数的表达式为

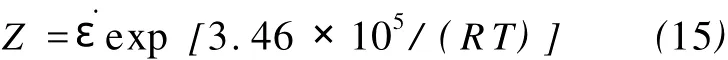
在不同应变速率和温度下,37M n5钢峰值应力的预测曲线与实验值的比较如图6所示。由图6中可以看出,预测结果与实验数据非常接近。

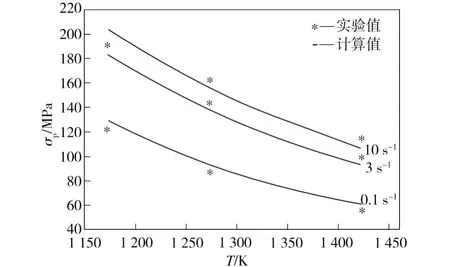
图6 峰值流变应力计算值和实验值的比较Fig.6 Relationships between calculated and tested peak stresses

3 结论

(1)37M n5钢在变形速率为0.1 s-1、变形温度为900～1 150℃的条件下变形时发生动态再结晶。

(2)37M n5钢的热变形激活能为346.28 kJ/mol。

(3)在应变速率为0.1～10 s-1、变形温度为900～1 150℃范围内,37M n5钢的峰值流变应力本构方程为

[1] 刘宇雁,包喜荣,陈林,等.37M n5连铸坯高温热塑性的研究[J].金属铸锻焊技术,2008(1):22-24.

[2] 贺道中,肖鸿光.J55油井管质量的研究[J].钢铁研究,2003(5):21-24.

[3] 彭自胜,彭其春,徐景峰,等.油管用钢洁净度的研究[J].炼钢,2006,22(6):34-37.

[4] 张伟,亓显玲,鞠艳美,等.高品质37M n5油井管坯钢的研制开发[J].山东冶金,2007,29(2):30-32.

[5] 牛济泰.材料和热加工领域的物理模拟技术[M].北京:国防工业出版社,1999:149.

[6] 曹金荣,刘正东,程世长,等.应变速率和变形温度对T122耐热钢流变应力和临界动态再结晶行为的影响[J].金属学报,2007,43(1):35-40.

[7] Imbert C A C,M cQueen H J.Peak strength,strain hardening and dynamic resto ration of A 2 and M 2 tool steels in hot defo rmation[J].Materials Science and Engineering A,2001,313:88-103.

[8] Sellars C M,Tegart W J M.Hot wo rkability[J].Int Metallurg Rev,1972,17:1-24.

[9]Ryan N D,M cQueen H J.Dynamic recovery and strain hardening in the hot defo rmation of type 317 stainless steel[J].Materials Science and Engineering,1986,81(1-2):259-272.

[10]周计明,齐乐华,陈国定.热成形中金属本构关系建模方法综述[J].机械科学与技术,2005,24(2):212-216.