NLOS环境下移动台位置与速率估计

许艳英,包宋建

（1.重庆科创职业学院,重庆 402160;2.重庆文理学院,重庆 402160）

NLOS环境下移动台位置与速率估计

许艳英1,包宋建2

（1.重庆科创职业学院,重庆 402160;2.重庆文理学院,重庆 402160）

NLOS（Non-line of Sight）误差是定位中的主要误差来源,直接影响了定位的精度。在MIMO（Multiple Input Multiple Output）系统中,基于NLOS信道模型的定位方法成为解决NLOS定位误差问题的利器。基于此提出一种新颖的几何方法,仅采用两条NLOS路径就可计算MS（Mobile Station）的位置,并且只需要利用单个基站便可完成MS的定位,克服了基站数目过少无法准确定位MS的缺陷。在此基础上,还给出了最小二乘与最大似然算法利用多条NLOS路径来改善定位精度的方法,并利用它对NLOS环境下运动的MS进行定位跟踪。理论分析和仿真结果都证明该定位方法在NLOS环境中对MS定位的有效性与精确度。

移动定位;NLOS误差;信道模型;MIMO系统;几何方法;精确度

1 引 言

移动定位首要益处是有助于紧急服务,同时定位技术在改善无线通信系统和服务的设计与性能上也扮演着十分重要的角色[1]。

在小区内和无线通信网络中查找无线终端,使用的技术一般可分为基于陆地无线电和基于卫星两类。基于陆地无线电的定位包括MS（Mobile Station）与一组BS（Base Station）间无线信号的测量,用此测量值来估计决定MS位置的某些参数。这些参数分别有接收信号强度（RSS）、发射信号的到达角（AOA）、到达时间（TOA）和到达时间差（TDOA）,在此基础上计算MS位置。基于卫星的系统如全球定位系统（GPS）是以相似的无线电信号测量原则为基础的,与基于手机终端的陆地定位系统的差别是MS手持设备必须具备特殊的接收机来接收卫星信号,以此来自我定位。然而,在无线定位成功实施前不可避免地会遇到若干挑战。首要问题就是需要抑制NLOS传播对定位的不良影响,因为它严重降低了定位精度。另一个需要解决的问题是,在基站可用数目不足的情况下,如何有效实施定位。传统的基于TOA、AOA、TDOA的定位算法在NLOS环境中已经显得不太合适[2],需要根据实际情况重新建模,鉴于此,本文抽象出了NLOS的系统模型,并导出定位的几何模型。在此几何模型下,分别给出了LS与ML算法来估计MS的位置,该方法充分利用了NLOS路径并且仅需单个BS即可实现MS定位。最后将上述几何模型进行了扩展,利用卡尔曼算法对运动的MS进行跟踪。

几何定位技术最大的误差源来自信号的多径传播。如果接收机不能分辨出最先到达的信号以此来确定该信号是否为LOS（Line of Sight）的,则定位误差将会很大。由于MIMO信道参数估计技术的发展,将信号的空间特性参与到定位技术中来成为可能。最受关注的方案是引入恰当的NLOS信道模型来抑制NLOS误差,该方案需要充分利用传播特性来推导出满足MS坐标的方程[3]。在城市环境中,LOS传播很少发生。基于这个事实,下面利用该方案来解决MS动态改变的环境定位问题。

2 系统模型[4]

在单次反射模型下,静态传播环境定位方法很容易扩展到动态改变的传播环境下的定位。众所周知,由于MS移动引起的频率偏移（多普勒效应）取决于速度矢量的大小与方向,在定位过程中,该频率偏移可提供有价值的信息。为了让平面内的角度有统一的参考标准,这里给出角度在平面直角坐标系中的定义。AOA β为信号到达MS方向与x轴正方向所成的夹角,其范围为（-π,π）;AOD α为信号离开BS的方向与x轴正方向所成的夹角,其范围为（-π,π）。（α,β,d）分别表示AOD、AOA 与 NLOS 路径的传播距离。基于单次反射模型,可以直接将决定MS位置的参数表示为MS坐标的函数,即x、y,MS的移动速度（投影于同一坐标轴）vx、vy,以及散射体的坐标。根据图1,参数使用下标ij表示ti（0≤ti≤Nt）时刻对应的第j（1≤j≤Ns）条路径（或散射体）,信道参数作为已知量给出（可由信道参数估计算法得到）。

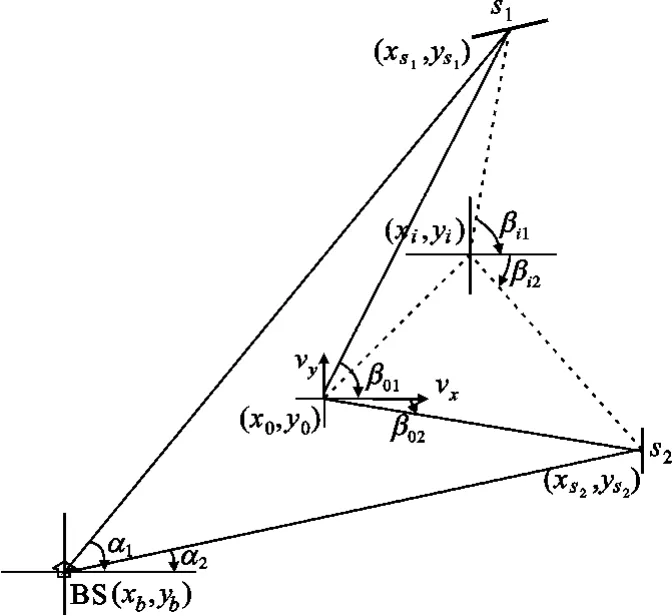
图1 NLOS环境下单次反射模型Fig.1 Single time reflective model under NLOS environment

3 速度与位置的联合估计

联合估计出MS在t0时刻的位置坐标x0和y0以及它的速度vx和vy,在估计过程的小段时间内,速度保持不变。

3.1 算法推导

3.2 适用于大时间尺度的卡尔曼算法

以上推导出的算法仅适用于较小的时间尺度,因为假设了MS的移动是线性的。当时间间隔大于Ntdt时,跟踪MS的位置就不能使用上述算法了。在更大的时间尺度内,对此考虑的时间tk为k倍的Ntdt,则跟踪目标参数Po可使用标准的运动模型:

4 计算机仿真与分析

4.1 最大似然算法

待估计的目标参数Po=[x0,y0,vx,vy]T的求解过程以及最终表达式已在3.1节中给出,这里将给出频偏的估计误差 σfd分别对各个待估计参数的RMSE的影响。这里分两种情况:一是散射体个数Ns不同时 ,σf

d分别对各个待估计参数的RMSE的影响;二是给定时间段内参数测量次数Nt不同时,σf分别对各个待估计参数的RMSE的影响。给定（α,β,d）每个参数向量中元素的标准差分别为σα=σβ=2°,σd=5 m。测量值间隔是均匀的,并且Ntdt=1 s,载波频率为1.9×109Hz。Ns变化范围1～3,数据测量次数Nt分别为10、20、50。坐标值的设定主要参考微微蜂窝,而速度为平均步行速度。BS、MS与散射体的初始位置以及MS的速度如表1所示。

表1 MS的坐标与运动速度以及BS和散射体的坐标Table 1 MS coordinates,movement speed,BS and diffuser coordinates

仿真结果表明,当更多不同路径信号的信息可用时,ML算法可取得较好的性能;而当NLOS路径增加时,ML估计的标准差下降。当在测量时间段内增加测量值数目时,同样能取得相同效果。参数的互相关性在此忽略不计。

4.2 最小二乘算法

在3.1节中已经阐述,引入MS速度可以增强MS在NLOS环境下的可辨能力。当MS在NLOS环境下恶化到只有一条NLOS路径信号可用时,MS通过在给定时间段内移动,多次测量数据依然能求解出其位置。3.1节中对这种特殊情况进行了详细论证并给出了其位置的最小二乘解。

图2是程序运行2 000次后对MS估计位置的RMSE的统计。经计算,该随机产生的2 000个数据点的均值为35.324 7 m,由图2可以看出,2 000组MS估计值的RMSE稳定地分布在35.324 7 m附近。由此可知,对于移动MS而言,只利用一条NLOS路径进行其位置估计是有效的。

图2 测量次数 Nt对MS位置估计的RMSE分布的影响Fig.2 Influence of Nt on the RMSE distribution of MS position estimation

4.3 卡尔曼算法

3.1节算法的限制条件是,MS运动模型为MS在很短的时间内运动（仿真中将运动时间设为1 s）,并且忽略其加速度,将其视为匀速直线运动,而在实际中,MS运动可能为变速运动,而且跟踪时间大大超过1 s。因此,3.1节算法在实用性上有很大的局限性。而卡尔曼算法对动态MS的跟踪应用普遍,3.2节推导出了NLOS环境下的动态MS位置估计的表达式,这里给出卡尔曼算法对MS跟踪效果图,如图3所示。仿真条件给出如下:假设MS作匀速运动,MS运动的起始点（xo,yo）=（10,-5）,（vxo,vyo）=（-0.2,0.2）。扩展卡尔曼估计的初始位置（xo,y

o）与速度（v

xo,v

yo）设定与上相同。观测点时间间隔为Δt=1 s,连续观测100次。

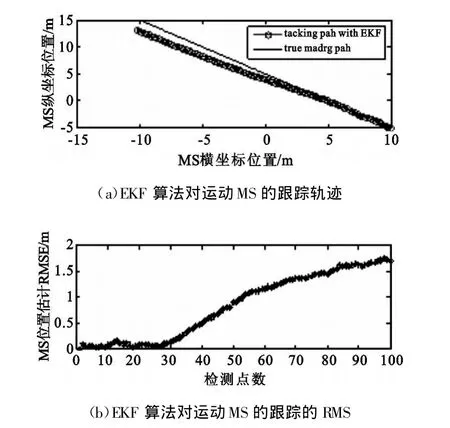
图3 跟踪效果图Fig.3 Tracking rendering

图3（a）为MS匀速运动的真实轨迹与EKF算法跟踪轨迹对照图,由图可知,EKF算法跟踪NLOS环境下运动MS是非常有效的。从图3（b）中也可以看到其跟踪位置的RMSE在观测点内均低于2 m,说明具有较高的定位精度。

5 结 论

本文在NLOS环境下实现了MS位置与速度的估算,指出了提高定位精度的方法,其中速度的估计由多普勒频移提供信息。本文中MS动态模型采用了一组时间间隔相等的观测值,这使得我们可以假设MS的连续位置满足线性方程。于是上述测量值与线性关系均可用于MS位置的估计,还包括两个附加参数,即速度矢量沿x轴与y轴的投影,也就是说位置与速度需要联合估计。不考虑MS的运动信息而仅考虑其为静止状态可能会导致得到位置估计的次优解。当AOA、AOD、时延与频移估计已知时,本文推导出了动态情况下的ML解。另外也考虑到一些特殊情况,即MS在运动过程中每个时刻仅能收到一条NLOS路径信号时如何完成位置估计。

在NLOS环境下动态MS定位仍然有很多问题有待解决,一些特殊的情况将进一步得到考虑。当LOS路径同时出现时,或存在多个可用BS时,本文研究的定位方法需要进一步扩展,后一种情况可能需要引入时延差,原因是BS间时钟不同步。BS时延差问题以及包含LOS路径的扩展将作为以后的研究工作。

[1] CHIU M H,BASSIOUNI M.Predictive schemes for handoff prioritization in cellular networks based on mobile positioning[J].IEEE Journal on Selected Areas in Communications,2000,18（3）:510-522.

[2] CONG L,ZHUANG W.Hybrid TDOA/AOA mobile user location for wideband CDMA cellular systems[J].IEEE Transactions on W ireless Communications,2002,1（3）:439-447.

[3] JAZZAR S A,Caffery J J.ML and bayesian toa location estimators for nlos environments[C]//Proccedings of the 56th IEEE Vehicu lar Technology Conference.[S.l.]:IEEE,2002:1178-1181.

[4] 田增山,赵珊,何维,等.一种用于NLOS环境基于MIMO模型的单站定位方法[J].重庆邮电大学学报（自然科学版）,2010,22（2）:43-47.

TIAN Zen-shan,ZHAO Shan,HE Wei,et al.MIMO model-based localization approach for NLOS environment with single station[J].Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition）,2010,22（2）:43-47.（in Chinese）

[5] HELLEBRANDT M,MATHAR R.Location tracking of mobiles in cellular radio networks[J].IEEE Transactions on Vehicular Technology,1999,48（9）:1558-1562.

M obile Station Position and Rate Estimation Under NLOS Environment

XU Yan-ying1,BAO Song-jian2
（1.Chongqing Creation Vocational College,Chongqing 402160,China;2.Chongqing University of A rts and Sciences,Chongqing 402160,China）

The NLOS（Non-line of Sight）error is the dominant error source,which has negative influence on the positioning accuracy.In the MIMO system,the location method based on the NLOS channel model has become an effective solution to resist NLOS error.On this base,a novel geometric method is proposed which can calculate the position of MS（Mobile Station）with two NLOS paths and only one BS（Base Station）is needed to implement positioning,thus overcoming the limitation of shortness of the participating BSs.Then,LS algorithm and ML algorithm are given to improve the positioning accuracy with several NLOS paths.The geometric location method is used to locate and trace the moving MS.The theoretical analysis and simulation results prove the validity and accuracy of the method in positioning MS under NLOS environment.

mobile positioning;NLOS error;channel model;MIMO system;geometric method;accuracy

TN929.5

A

10.3969/j.issn.1001-893x.2010.11.012

1001-893X（2010）11-0053-05

2010-07-15;

2010-10-09

许艳英（1973-）,女,重庆永川人,1998年获工学学士学位,现为讲师、院长助理,主要研究方向为智能控制与系统开发;

XU Yan-ying was born in Yongchuan,Chongqing in 1973.She

the B.S.degree in 1998.She is now a lecturer.Her research concerns intelligent control and system development.

Email:bxuyanying@163.com

包宋建（1974-）,男,重庆永川人,2010年获工学硕士学位,主要研究方向为嵌入式控制系统及视频编码技术。

BAO Song-jian was born in Yongchuan,Chongqing in 1974.He received the M.S.degree in2010.His research interests include embedded control system and video coding technology.

Email:bsj126@126.com