“雨滴下落”和“伞兵空降”——谈直线运动中的两种典型变加速运动模型

李晶

(淮阴中学 江苏 淮安 223001)

高中物理研究的直线运动主要是匀变速运动和简单的变加速运动，而在变加速直线运动中有两种最典型且最基本的模型，即“雨滴下落”模型和“伞兵空降”模型.

1 模型一——雨滴下落模型

一质量为m的雨滴在高空由静止开始下落，设下落过程中受到的空气阻力与雨滴下落速率成正比，即f=kv，重力加速度为g.

【问题1】求解雨滴下落的终极速度.

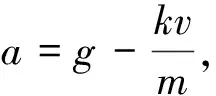
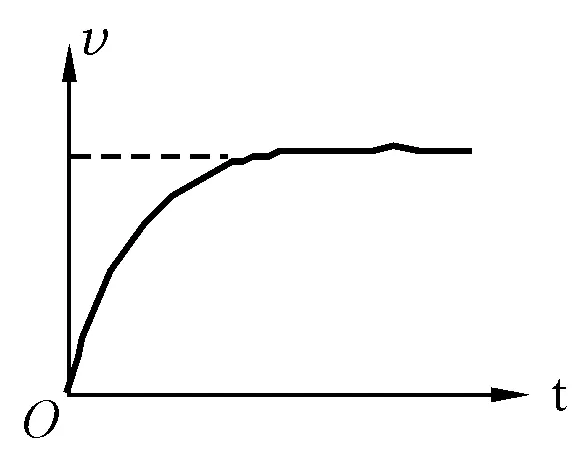
图1

【问题2】设雨滴从静止下落到速度最大所用时间为t，求解雨滴达到终极速度前下落的位移x.

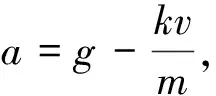
等式两边求和

即

而

解得

【模型应用1】如图2所示，水平放置的两根光滑平行金属导轨置于垂直于导轨平面的匀强磁场中，磁感应强度为B，导轨间距为L.导轨左端连接一电阻，阻值为R.有一质量为m的金属棒放置在导轨平面上，并与导轨垂直，在恒定拉力F的作用下由静止开始运动，经过时间t，金属棒速度达到稳定，棒与导轨电阻均不计.求：(1)金属棒最终的稳定速度；(2)金属棒达到稳定速度前通过的位移.

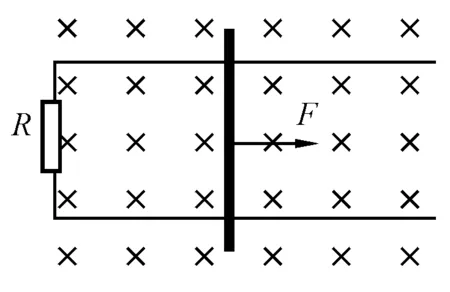
图2

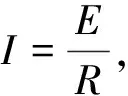
当a=0时，最大速度

等式两边同乘Δt得

两边同时求和得

解得通过的位移

【模型应用2】如图3所示，PQ为一根足够长的绝缘细直杆竖直固定，空间充满磁感应强度为B的水平匀强磁场，方向垂直纸面向里.一个质量为m，带有正电荷的小球套在PQ杆上，小球可沿杆滑动，球与杆之间的动摩擦因数为μ，小球带电荷为+q，重力加速度为g.现将小球由静止开始释放，经过时间t达到最大速度，试求：小球在沿杆下滑过程中(1)最大速度；(2)从释放到达到最大速度的位移.

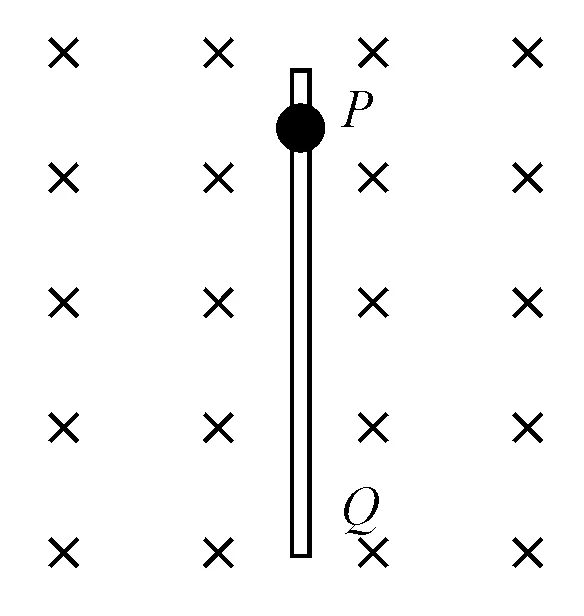
图3

【解析】当a=0时速度最大，即

解得

小球由静止释放做加速度减小的加速运动，其加速度

两边同乘Δt，得

两边同时求和，得

解得从释放到速度最大时的位移为

【模型总结】高中阶段除了“雨滴下落”和电磁感应中导体棒的运动、磁场中带电体的运动等，还有很多类似的例子.其实从运动过程来看都是加速度逐渐减小的加速直线运动，最终的稳定态加速度为零，速度最大.

2 模型二——伞兵空降模型

一质量为m的伞兵从足够高的高空跳下，加速运动到一稳定速度v0后打开降落伞，此后受到的空气阻力与伞兵速率成正比，即f=kv，重力加速度为g.

【问题1】求解伞兵最终的速度.

【解析】伞兵跳下后可看作先经历一加速运动直至速度v0，加速过程类似于雨滴下落.开伞后由于初速度很大，空气阻力大于重力，做减速运动且

kv-mg=ma

随着速率的减小，加速度a逐渐减小，最终当a=0时，伞兵达到最小速度，即终极速度

伞兵做的是加速度逐渐减小的减速运动，此过程的v-t图像如图4所示.

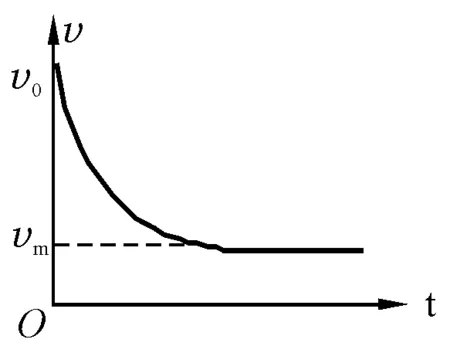
图4

【问题2】设伞兵从开伞到速度最小所用时间为t，求解伞兵从开伞到速度最小时的位移x.

【解析】此过程伞兵做的是变加速直线运动.根据牛顿第二定律知伞兵加速度

即加速度随v线性变化.设时间微元为Δt，可得

等式两边求和得

而

解得

【模型应用1】如图5所示，水平放置的两根平行金属导轨置于垂直于导轨平面的匀强磁场中，磁感应强度为B，导轨间距为L.导轨左端连接一电阻，阻值为R.有一质量为m的金属棒放置在导轨平面上，并与导轨垂直.棒以初速度v0开始运动，经过时间t后停下，棒与导轨电阻均不计，棒与导轨间动摩擦因数为μ，求：金属棒整个过程通过的位移.

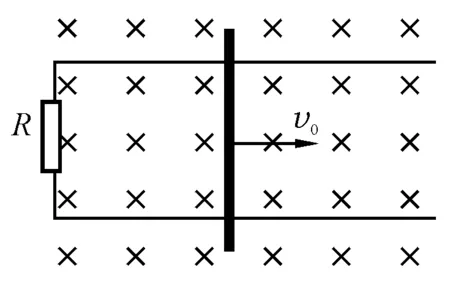
图5

【解析】由牛顿第二定律，有

得

等式两边同乘Δt，得

求和后得

解得棒通过的位移

【模型应用2】跳伞运动员从2 000 m高空跳下，在开始下落的过程中未打开降落伞.设初速度为零，所受空气阻力与下落速率关系为f=k1v，k1>0，加速至获得稳定速度为vm=50 m/s时运动员离地面高度s=200 m，此后打开降落伞，在2 s内速度减小到v1=5 m/s，达到稳定，此过程所受空气阻力与下落速率的关系为f=k2v，k2>0，然后匀速下落到地面.求：(1)运动员打开降落伞后运动的时间(2)运动员在空中运动的总时间.

【解析】打开伞前运动员做加速运动至速度为vm，此时

k1vm=mg

(1)

而此加速过程中

(2)

(3)

即

(4)

其中

x1=(2 000-200) m=1 800 m

联立解得

t1=41 s

开伞后运动员做减速运动至速度为v1，此时

k2v1=mg

(5)

而此减速过程中

(6)

(7)

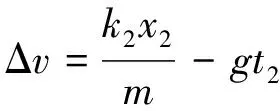
(8)

联立解得开伞后减速运动的位移

x2=32.5 m

则匀速运动的时间

所以打开伞后的运动时间为

t2+t3=35.5 s

运动员在空中运动的总时间为

t1+t2+t3=76.5 s

【模型总结】“伞兵空降”模型从运动过程来看是加速度逐渐减小的减速直线运动，最终的稳定态加速度为零，速度最小.

3 模型总结

在高中阶段会接触很多变加速直线运动，大多数属于这两类比较基本模型.在解决一些新情境的题目时如果能够准确识别运动的特点，解决问题就变得容易许多.其实这两类模型从本质上看都是变加速直线运动，且加速度与速度呈线性关系.通过对加速度表达式两边同乘以时间微元Δt的方法，再两边求和，从而得出速度变化量Δv、位移x、运动总时间t这三者之间的关系，在题目中根据已知量求解未知量，解决问题.此方法也是江苏高考近几年的考查热点.