做好两个回归 简化速度计算

傅贤武

(宁波市北仑区江南中学 浙江 宁波 315821)

物理概念和物理规律是严谨、科学的，同时也是理性、抽象的.在物理概念和物理规律教学时，知识的获取主要是感知和概括.在物理习题教学时，知识的应用主要是类比和迁移.如何让初二学生、特别是数学基础不太好的学生做好有关速度计算习题？我尝试做好两个回归——回归感性认识和回归形象思维，帮助学生简化速度计算.

1 从理性回归感性——赋值法

大多数初二学生对于符号运算和比例计算不太熟练，容易出错.我建议他们采用赋值法，从理性的严谨计算回归感性的验证计算.

解法一：理性的严谨计算

解法二：赋值法

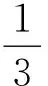
中间一半也就是60 m，所用时间

最后还有20 m，所用时间

所以，平均速度

【例2】三位同学的速度之比为1∶2∶3，则他们走完相同的路程所需时间之比为

A.6∶3∶2 B.3∶2∶1

C.1∶2∶3 D.2∶3∶6

解法一：理性的严谨计算

解法二：赋值法

不妨假设v1=1 m/s，v2=2 m/s，v3=3 m/s，s=6m.显然，t1=6 s，t2=3 s，t3=2 s.当然选A.

2 从抽象回归形象——作图法

一般来说，物理计算都是在一定情景下的计算，并且这个情景大多是通过文字叙述表达的.然而，对于很多初二学生来说，要真正理解一大段抽象的文字所表达的情景，是有一定难度的.建议采用作图法，从抽象的文字叙述回归形象的物理情景.

【例3】甲和乙两人进行百米赛跑，他们同时出发，甲到达终点时，乙还剩10 m.假设他们都以原来的速度跑，将甲的起跑线向后移动10 m，乙仍然在原来的起跑线，两人同时出发，结果是

A.甲先到 B.乙先到

C.同时到 D.无法确定

解法一：严格证明，需要用不等式知识，对初二学生来讲，不好理解.略.

解法二：赋值法，可以很好解决，上面已经介绍.

亦略.

解法三：作图法.甲和乙第一次比赛结果如图1(a)所示.

显然，甲的速度比乙大.

甲和乙第二次比赛过程如图1(b)所示.

根据图1(b)，甲到达A点时，乙到达B点，此时甲和乙距离终点都恰好还剩10 m路程.由于甲的速度比乙大，所以甲先到终点.

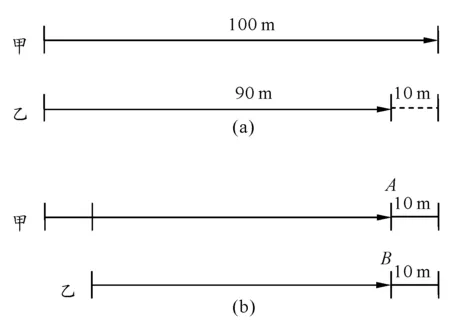
图1

【例4】甲乙两人从同一座桥的同一端出发，到达另一端.甲前一半路程跑，后一半路程走；乙前一半时间跑，后一半时间走.假设甲乙走和跑的速度一样，问谁先到达.

解：作图法.甲的运动过程如图2(a)所示.

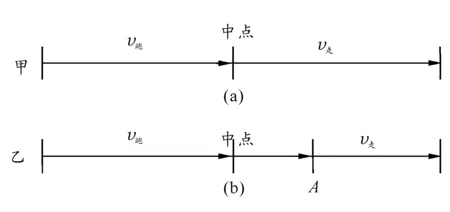
图2

因为乙前一半时间跑，后一半时间走，所以乙要跑过中点，不妨假设乙跑到A点后开始走，且t跑=t走.则乙的运动过程如图2(b)所示.

比较图2(a)和2(b)，起点到中点那一段，甲和乙都是跑；A点到终点那一段，甲和乙都是走；他们不同之处就在于中点到A点那一段，甲是走，而乙是跑，所以乙先到.