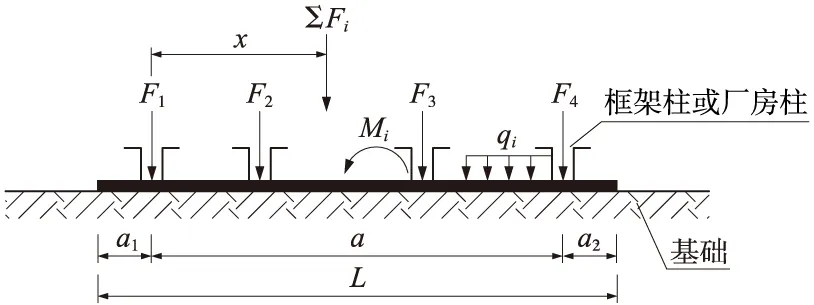
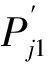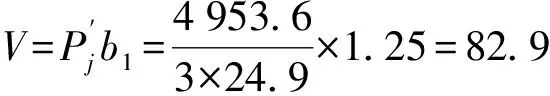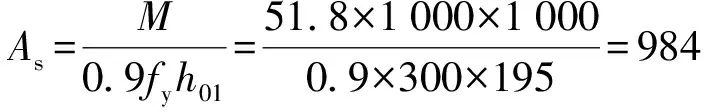按上述确定a1和a2后,使偏心地基净反力变为均布地基净反力,其值为
式中Pj——均布地基净反力设计值。
由此也可得到一个合理的基础长度L。
2.2 确定基础底板宽度b
由确定的基础长度L和假定的底板宽度b,根据地基承载力设计值f,一般可按两个方向分别进行如下验算,从而确定基础底板宽度b。
基础底板纵向边缘地基反力
应满足
基础底板横向边缘地基反力
应满足
式中pmax和pmin——基础底板纵向边缘处最大和最小地基反力设计值;
p′max和p′min——基础底板横向边缘处最大和最小地基反力设计值;
G——基础自重设计值和其上覆土重标准值之和,可近似取G=20b×L×D,D为基础埋深,但在地下水位以下部分应扣去浮力;
∑M′——作用于基础上各竖向荷载、横向弯矩对基础底板横向中点产生的总弯矩设计值;
其余符号同前述。
当∑M′=0时,则只须验算基础底板纵向边缘地基反力;
当∑M=0时,则只须验算基础底板横向边缘地基反力;
当∑M=0且∑M′=0时(即地基反力为均布时),则按下式验算,很快就可确定基础底板宽度b。
式中p——均布地基反力设计值。
2.3 求基础梁处翼板高度并计算其配筋

图2 基底横向净反力示意
基础底板横向边缘处地基净反力
式中S——从基础纵向边缘最大地基反力处开始到任一截面的距离。
其余符号同前述,需要指出的是这个公式考虑了条形基础双向偏心受力的影响。
基础梁边处翼板地基净反力
基础梁边处翼板每米宽弯矩
基础梁边处翼板每米宽剪力
若∑M′=0时,则上述M,V表达式为
若∑M=0时,则上述M,V表达式为
若∑M=0和∑M′=0时,则上述M,V表达式为
基础梁边处翼板有效高度
基础梁边处翼板截面配筋
式中 ft——混凝土轴心抗拉强度设计值;
fy——钢筋抗拉强度设计值;
其余符号同前述。
2.4 抗扭
当上述∑M′≠0时,对于带有翼板的基础梁,一般可以不考虑抗扭计算,仅从构造上将梁的箍筋做成闭合式;反之,则应进行抗扭承载力计算。
3 静力平衡法和倒梁法的应用
在采用静力平衡法和倒梁法分析基础梁内力时,应注意以下问题。
(1)由于基础自重和其上覆土重将与它产生的地基反力直接抵消,不会引起基础梁内力,故基础梁的内力分析用的是地基净反力,这在基础梁边翼板的配筋计算中已有所体现。
(2)对a1和a2悬臂段的截面弯矩可按以下两种方法处理:①考虑悬臂段的弯矩对各连续跨的影响,然后两者叠加得最后弯矩,②倒梁法中可将悬臂段在地基净反力作用下的弯矩全由悬臂段承受,不传给其他跨。
(3)两种简化方法与实际均有出入,有时出入很大,并且这两种方法同时计算的结果也不相同,建议对介于中等刚度之间且对基础不均匀沉降的反应很灵敏的结构,应根据具体情况采用一种方法计算的同时,采用另一种方法复核比较,并在配筋时作适当调整。
(4)由于建筑物实际多半发生盆形沉降,导至柱荷载和地基反力重新分布,研究表明[11~13]:端柱和端部地基反力均会加大,为此宜在边跨增加受力纵筋面积,并上下均匀配置。
(5)为增大底面积及调整其形心位置使基底反力分布合理,基础的端部应向外伸出,即应有悬臂段。
(6)一般计算基础梁时翼板混凝土对基础梁结构承载力的影响很小,因此可不考虑翼板作用。
3.1 静力平衡法
静力平衡法是假定地基反力按直线分布不考虑上部结构刚度的影响,根据基础上所有的作用力按静定梁计算基础梁内力的简化计算方法。
3.1.1 静力平衡法具体步骤
(1)先确定基础梁纵向每米长度上地基净反力设计值,其最大值为Pjmax×b,最小值为Pjmin×b,若地基净反力为均布则为Pj×b,如图3中虚线所示。

图3 基础梁荷载示意
(2)对基础梁从左至右取分离体,列出分离体上竖向力平衡方程和弯矩平衡方程,求解梁纵向任意截面处的弯矩MS和剪力VS,一般设计只求出梁各跨最大弯矩和各支座弯矩及剪力即可(图4)。

图4 计算隔离体
3.1.2 静力平衡法适用条件
地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足
且上部结构为柔性结构时的柱下条形基础和联合基础,用此法计算比较接近实际。其中lm为基础梁上的平均柱距,ks为基床系数,可按ks=p0/s0计算,其中p0为基础底面平均附加压力标准值,s0为以p0计算的基础平均沉降量,也可参照各地区性规范按土类名称及其状态已给出的经验值,b0和I分别为基础梁的宽度和截面惯性矩,Ec为混凝土的弹性模量。
3.2 倒梁法
倒梁法是要求上部结构完全刚性,各柱间无沉降差异,将柱下条形基础视为以柱脚作为固定支座的倒置连续梁,以线性分布的基础净反力作为荷载,按多跨连续梁计算法求解内力的计算方法。
3.2.1 倒梁法具体步骤
(1)先用弯矩分配法或弯矩系数法计算出梁各跨的初始弯矩和剪力,弯矩系数法比弯矩分配法简便,但它只适用于梁各跨度相等且其上作用均布荷载的情况,它的计算内力表达式为
式中,δ,ξ分别为弯矩系数和剪力系数,Pj×b即是基础梁纵向每米长度上地基净反力设计值,其中弯矩系数和剪力系数按所计算的梁跨数和其上作用的均布荷载形式,直接从建筑结构静力计算手册中查得,l为梁跨长度,其余符号同前述。
(2)调整不平衡力,由于倒梁法中的假设不能满足支座处静力平衡条件,因此应通过逐次调整消除不平衡力。
首先,由支座处柱荷载Fi(图5)和求得的支座反力Ri(图6)计算不平衡力ΔRi
式中 ΔRi——支座i处不平衡力;
V左i,V右i——支座i处梁截面左、右边剪力。
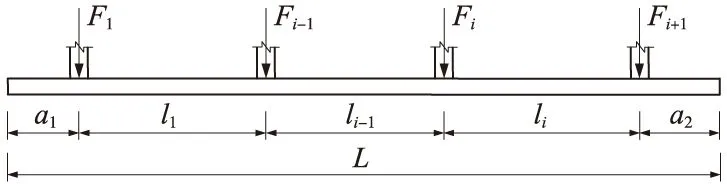
图5 柱荷载Fi

图6 支座反力与计算简图
其次,将各支座不平衡力均匀分布在相邻两跨的各1/3跨度范围内,如图7(实际上是调整地基反力使其成阶梯形分布,更趋于实际情况,这样各支座上的不平衡力自然也就得到了消除),Δqi按下式计算
对于边跨支座
对于中间支座
式中 Δqi——支座i处不平衡均布力;
li-1,li——支座i左右跨长度。
继续用弯矩分配法或弯矩系数法计算出此情况的弯矩和剪力,并求出其支座反力与原支座反力叠加,得到新的支座反力。

图7 调整不平衡力荷载Δqi
(3)重复步骤(2),直至不平衡力在计算容许精度范围内,一般经过一次调整就基本上能满足所需精度要求了(不平衡力控制在不超过20%)。
(4)将逐次计算结果叠加即可得到最终弯矩和剪力。
3.2.2 倒梁法适用条件
(1)地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足lm≤1.75/λ(符号同静力平衡法所述),且上部结构刚度较好时的柱下条形基础,可按倒梁法计算。
(2)基础梁的线刚度大于柱子线刚度的3倍,即
式中EC——混凝土弹性模量;
IL——基础梁截面惯性矩;
H,IZ——分别为上部结构首层柱子的计算高度和截面惯性矩;
(3)同时各柱的荷载及各柱柱距相差不多时,也可按倒梁法计算。
4 算例
我国新建高速客运专线多采用板式无砟轨道,轨道板制造加工精度高,对线下和线上存板台座要求严格,因此存板台座的设计必须引起高度重视。下面结合沪杭铁路CRTSⅡ型无砟轨道板场的存板要求和上海市松江区的地质特征,按照上述设计方法给出一个工程算例。
每个台位最多存板12块,台位间距为3 050 mm,下面以板场典型8个台位并排为例,每块板重按86 kN计算,恒载分项系数取1.2,与板重相比现场施工活荷载很小,可以忽略不计。作用在单个条基上的竖向合力∑Fi=1.2×86/2×8×12=4 953.6 kN,台座位置按条基中心对称布置,因此竖向荷载对条基中心产生的综合弯矩为零。地基承载力设计值为80kPa。
4.1 确定基础长度
因为台座位置按条基中心对称布置,所以基底净反力均匀,基础长度定为
L=3.05×7+2.55+0.5×2=24.9 m
4.2 确定基础底板宽度
假定底板宽度为3 m,基底反力
73.3kN/m2<80kPa
4.3 求基础梁处翼板高度并计算其配筋
基础梁边处翼板每米宽弯矩
基础梁边处翼板每米宽剪力
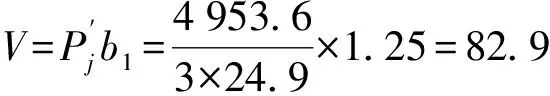
基础梁边处翼板有效高度
这里取底板厚度为250 mm,因此h01=250-55=195 mm
基础梁边处翼板截面配筋
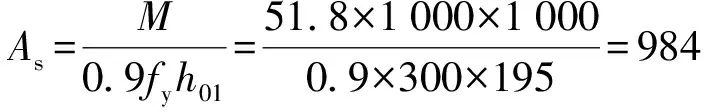
因此翼板横向配置φ14mm、间距为150mm的HRB335钢筋。
4.4 计算基础梁配筋
这里轨道板通过方木垫块支承在基础梁上,其刚度对基础梁的影响可以忽略不计,因此可以采用静力平衡法计算基础梁配筋,计算简图见图8。

图8 基础梁计算简图(单位:kN)
由有限元程序ANSYS计算得到的条基内力如图9所示。
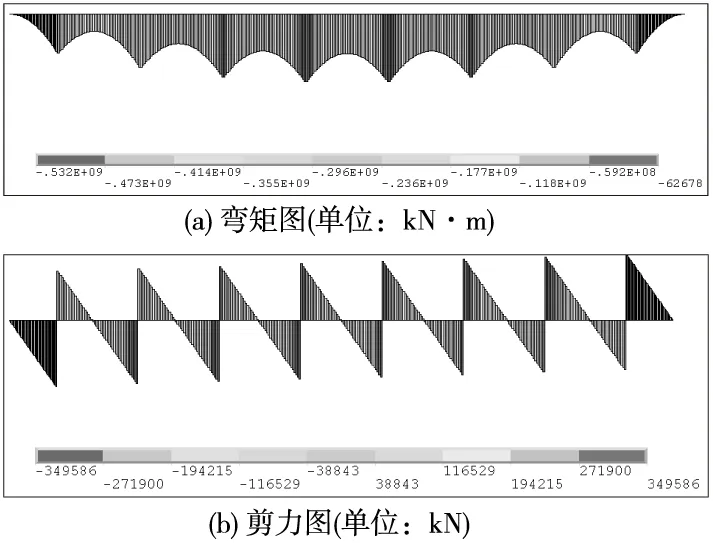
图9 基础梁内力图
因此支座和跨中最大弯矩和剪力分别为532 kN·m和698 kN。
由此计算基础梁和配筋,最终得到条形基础的配筋如图10所示。

图10 条形基础配筋(单位:mm)
5 讨论
5.1 关于静力平衡法
(1)由于静力平衡法不考虑基础与上部结构的相互作用,因而在荷载和直线分布的基底反力作用下可能产生整体弯曲。与其他方法比较,这样计算所得的基础梁不利截面的弯矩绝对值一般还是偏大。
(2)静力平衡法适用条件中要求上部结构为柔性结构,如何判断上部结构为柔性结构,从绝大多数建筑的实际刚度来看均介于绝对刚性和完全柔性之间,目前还难以定量计算。在实践中往往只能定性地判断其比较接近哪一种极端情况,例如,剪力墙体系的高层建筑是接近绝对刚性的,而以屋架—柱—基础为承重体系的排架结构和木结构以及轨道板存放台座基础等是接近完全柔性的。具体应用上,对于中等刚度偏下的建筑物也可视为柔性结构,如中、低层轻钢结构,柱距偏大而柱断面不大且楼板开洞又较多的中、低层框架结构,以及体型简单,长高比偏大(一般大于5以上)的结构等等。
5.2 关于倒梁法
(1)满足倒梁法适用条件之一的条形基础一般都能迫使地基产生比较均匀的下沉,与假定的地基反力按直线分布基本吻合。
(2)由于假定中忽略了各支座的竖向位移差且反力按直线分布,因此在采用该法时,相邻柱荷载差值不应超过20%,柱距也不宜过大,尽量等间距。另外,当基础与地基相对刚度愈小,柱荷载作用点下反力会过于集中成“钟形”,与假定的线性反力不符;相反,如软弱地基上基础的刚度较大或上部结构刚度大,由于地基塑性变形,反力重分布成“马鞍形”,趋于均匀,此时用倒梁法计算内力比较接近实际。
(3)实际工程中,有一些不需要算得很精很细,有时往往粗略地将第一步用弯矩分配法或弯矩系数法计算出的弯矩和剪力直接作为最终值,不再进行调整不平衡力。这对于中间支座及其中间跨中来说是偏于安全的,而对于边跨及其支座是偏于不安全的。从几个等跨梁算例来看,一般情况下,多次调整不平衡力(此项较繁琐),结果使中间支座的内力(指弯矩,剪力)及其跨中弯矩有所减小,边跨支座剪力及其跨中弯矩有所增加,但增减幅度都不大。因此,若不进行调整平衡力,建议根据地区设计经验适当增大边跨纵向抗弯钢筋,其幅度5%左右,这在某些精度范围内一般可以满足设计要求,另外由于各支座剪力值相差不大(除边支座外),也可取各支座最大剪力值设计抗剪横向钢筋,当然每跨的中间可以放宽。
静力平衡法和倒梁法的核心计算过程为超静定连续梁的求解问题,目前各种计算分析软件(结构力学求解器、SAP2000、ANSYS等)都能精确便捷的求解,这也大大降低了工程设计的复杂程度。
[1]GB50007—2002,建筑地基基础设计规范[S].
[2]朱炳寅,等.建筑地基基础设计方法及实例分析[M].北京:中国建筑工业出版社,2007.
[3]陈希哲.土力学地基基础[M].北京:清华大学出版社,2004.
[4]徐长节.地基基础设计[M].北京:机械工业出版社,2007.
[5]顾晓鲁.地基与基础[M].北京:中国建筑工业出版社,2003.
[6]郭继武.地基基础设计简明手册[M].北京:机械工业出版社,2008.
[7]黄平干,等.柱下条形基础简化计算及其设计步骤[J].工程建设与设计,1999,196(4):8-12.
[8]刘 伟.岩石地基上扩展式基础基底反力分布数值分析[J].山西建筑,2009,35(1):114-115.
[9]朱爱军,等.岩石地基上扩展基础基底反力分布的分析[J].工业建筑,2004,34(4):53-56.
[10]孙文科.建筑物基底反力的实时监测与分析[J].地震学刊,2001,21(2):30-33.
[11]艾智勇,等.分层地基上举行刚性基础的基底反力、沉降和倾斜计算[J].力学季刊,2008,29(1):113-119.
[12]宋建学,等.某高层建筑基底反力及柱轴力监测与分析[J].武汉理工大学学报,2007,29(2):69-74.
[13]阴 可,等.岩石地基上扩展基础的基底反力实测分析[J].重庆建筑大学学报,2006,28(6):72-74.