采用流固耦合方法数值分析减压器动态响应①

何德胜,郭 正,鲍福廷,李广武

(1.西北工业大学航天学院,西安 710072;2.国防科技大学航天与材料工程学院,长沙 410073;3.中国航天科技集团公司四院401所,西安 710025)

0 引言

减压器是一种能够根据上游气体的压力自动调节自身活门的开度,从而使下游出口的气体压力保持稳定的机械装置,被广泛用于航天飞行器燃料箱压力保持和地面试车台气源供气系统,起着重要的控制和调节作用。本文研究了一种用于固体冲压发动机地面试车台的减压器。其在不工作时处于常开状态,工作时高压气体由进气口进入高压腔,然后通过主活塞座上的孔道进入低压腔,当低压腔压力高于预定值时,主膜片所受气压力大于弹簧力,从而向下方运动,此时主活塞在副弹簧的推动下也向下运动,使活门开度减小,低压腔压力随之减小。通过这种自动调整,低压腔压力可维持在设定值。弹性运动部件中的活塞顶杆和膜片硬芯既可独立运动,也可贴合在一起运动,并可能发生碰撞,导致减压器的内部结构非常复杂。在上游压力开启作用的极短时间内,减压器内部结构受到冲击,伴随弹性敏感元件的运动,内部气体流动必然是非定常的,并且与结构的运动相耦合,有可能表现出强烈的非线性波动,严重时甚至导致膜片破裂,使减压器失去功能。因此工程上迫切需要采用流固耦合数值模拟技术对减压器系统进行数值分析。目前国外对于管路阀门系统动态特性的研究已经开始大量采用非定常计算流体力学(CFD)技术,分析阀门内部流动参数的非定常、非线性特性,如文献[1]。近年来,为了研究阀门开闭过程中的动态特性,HOSANGADI与CAVALLO[2-3]采用动网格技术模拟阀门内部结构运动与流体的耦合特性,目前其采用的固体运动模型主要是已知运动规律的刚体模型。国内采用CFD技术研究阀门流动特性仍以定常问题为主[4-5],对于水锤等瞬态问题的研究主要采用特征线方法[6-7],该方法难以得出三维空间中流场参数随时间变化的规律,存在一定的局限性。

本文模拟减压器动态特性采用流固耦合方法,流场计算采用三维非定常Euler模型,固体结构变形采用一维质量弹簧模型。

1 数值方法

1.1 控制方程

某固体冲压发动机地面试车台的减压器结构外形及计算机网络如图1所示。其主要由高压腔、低压腔及弹性运动部件组成,弹性运动部件包括活塞顶杆和膜片硬芯两部分。

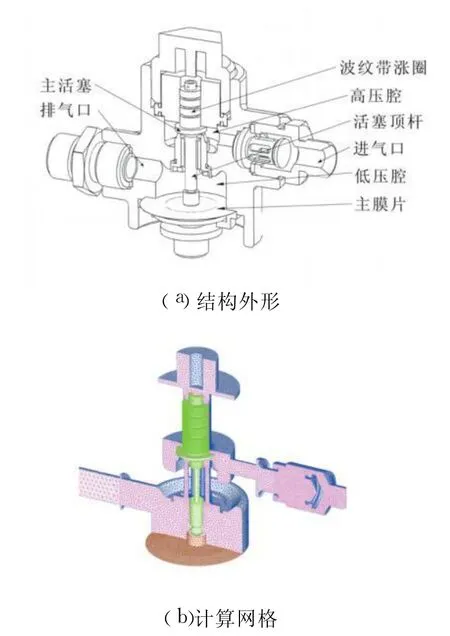
图1 减压器结构外形及计算网格Fig.1 Geometry and computational grids of a pressure regulation value

ALE(Arbitrary Lagrangian-Eulerian)有限体积描述下的三维可压缩非定常Euler方程可表示为如式(1)的积分形式:

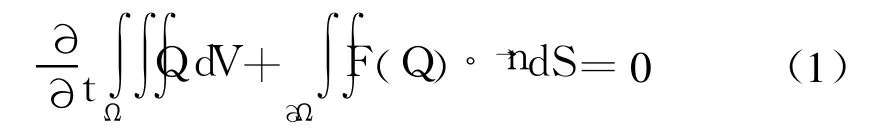
其中,Ψ是控制体;∂Ψ是控制体边界;→n为控制体边界外法向单位向量;守恒变量Q和对流项为

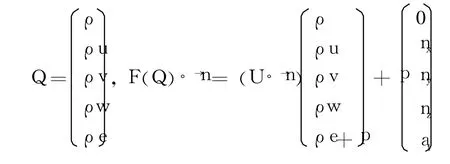
式中 U为流体相对于网格的速度;at为网格运动的法向速度;nx、ny、nz是→n的3个分量。

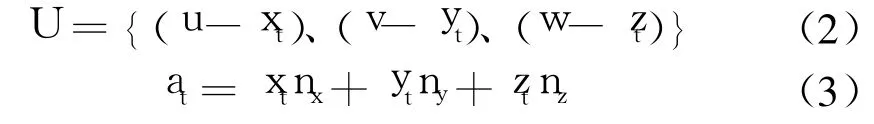
式中 xt、yt、zt分别是网格运动速度的3个分量。

1.2 离散方法

在控制体(三维网格单元)内积分式(1),有

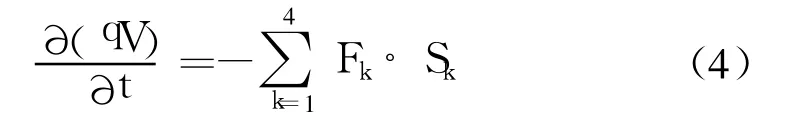
式中 m表示时间层;Sk是第k个积分面的矢量面积。

为得到积分面上对流项通量的二阶近似,首先采用泰勒展开法,由单元中心处向积分面中心对基本变量进行重建,然后用通量矢量分裂方法(Van-Leer或Steger分裂法)解决积分面上的Riemann问题,即

其中,q表示基本变量,q=(ρ,u,v,w,p)T基本变量的重建值由式(6)计算:

式中 φij是限制器。

采用传统的格林公式方法求解变量梯度,即

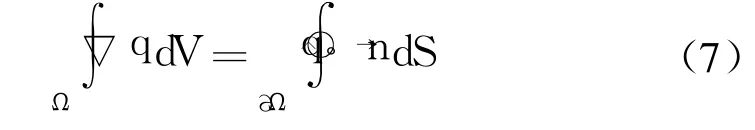
以三维网格单元为控制体,近似计算式(7)右端的面积分,可得单元中心处的变量梯度:

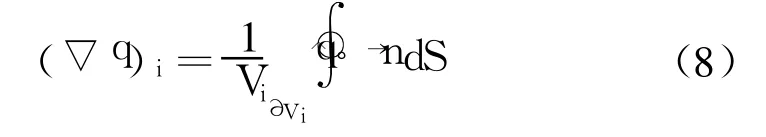
上述公式中的变量定义见图2。为了抑制流场中物理量间断处可能出现的数值振荡,本文改进了Barth和Jespersen[8]的通量限制器。

1.3 对虚拟挡板面的积分

采用动网格技术真实模拟弹性敏感元件的动态过程,然而活门关闭时与活门座接触,微微开启时与活门座分离,这一过程中计算域拓扑发生变化,动网格处理比较复杂且费时。接触问题是目前动网格技术的难点,一些涉及动网格技术的商业软件都未很好解决这一问题。为实现对活门关闭∕开启过程的数值模拟,本文提出了可变边条零厚度虚拟挡板技术。即在网格生成时人为地在活门与活门座之间布置一个无厚度的挡板,当活门关闭时给该挡板面双向赋壁面条件,当活门部分开启时则根据实际开度计算出开启部分所占的面积比,计算通量时认为开启部分是内部积分面,作通气处理。

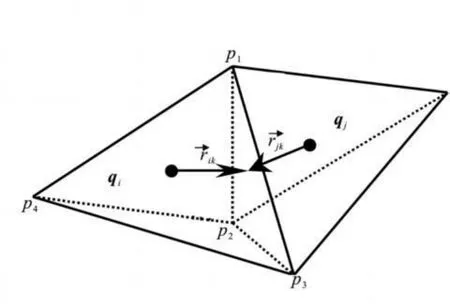
图2 变量定义方式示意图Fig.2 Definition of variables

式(4)是对流场中一般网格单元的离散形式,等号右边的求和是对四面体单元的4个三角形表面进行的。如果网格单元的某一个表面位于虚拟挡板上,不失一般性,假设图2中单元i的p1p2p3表面位于虚拟挡板上,则式(4)对于单元i应改写为

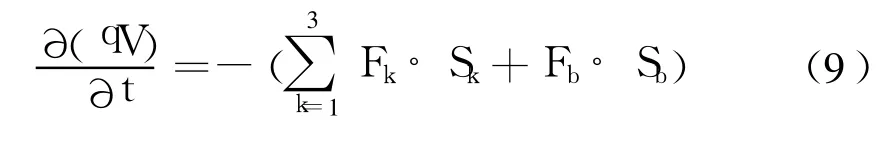
式(9)中等号右边的两项分别为3个一般表面的通量求和以及位于虚拟挡板上的表面的通量。Sb、Fb分别是位于虚拟挡板上的表面的面积和其中心处的对流项。

图3是p1p2p3表面在虚拟挡板上的示意图,图3中预置的虚拟挡板宽度为2层网格,某时刻物体间的实际距离为阴影部分所示,此时三角形p1p2p3上阴影部分作通气处理,而其他部分作壁面处理。于是有

式中 Sf、Sw分别是通气部分和壁面部分的面积。

对流项Fb按下面的方法计算:

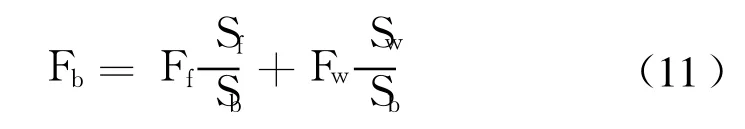
式中 Ff是作为通气的内部单元面时该表面上的对流项,由式(5)计算得到;Fw是作为壁面时该表面上的对流项。

Fw对表面的通量积分由式(12)计算:

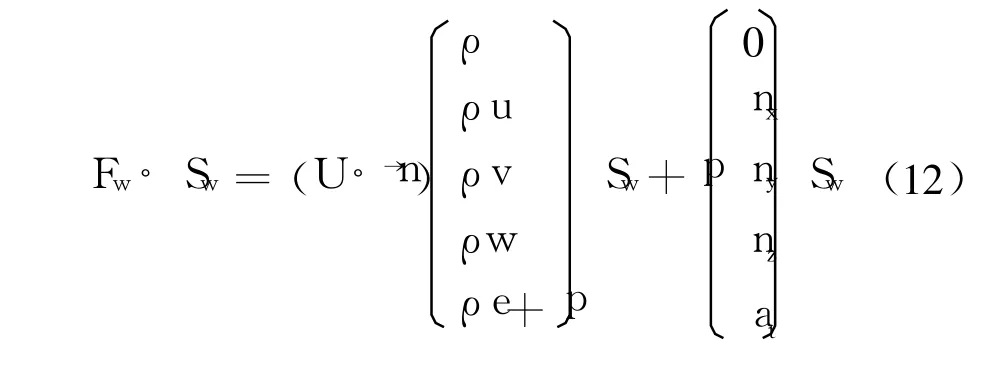
对壁面采用无粘流的无穿透条件,即U·→n=0,则式(12)简化为

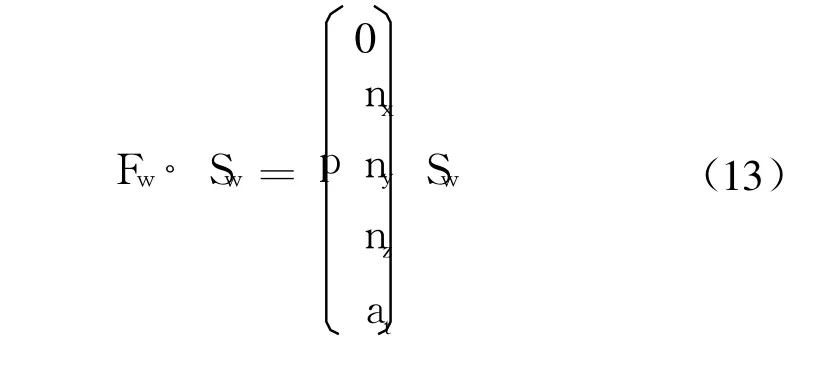
计算通量积分时对流项F应取积分面上的平均值,可以证明,对于三角形积分面,其中心处的物理量值是整个面上平均值的二阶近似,因此对于二阶格式,可采用三角形中心处的对流项。对于具有虚拟挡板表面的网格单元,应该针对该表面通气和壁面2种状态分别求解变量梯度,计算对流项Ff和Fw时分别采用相应的梯度进行基本变量的重建。

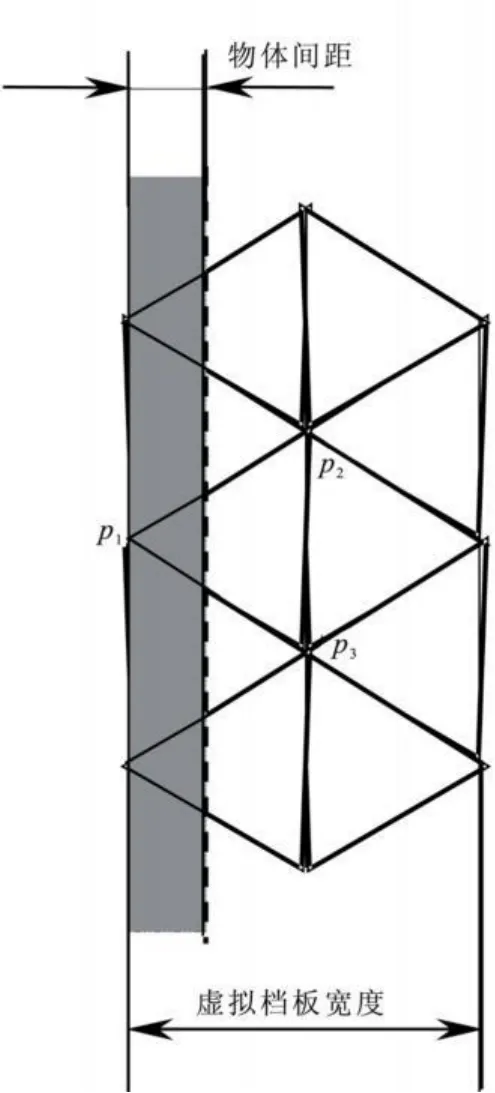
图3 虚拟挡板示意图Fig.3 Sketch of virtualbaffle faces

时间离散采用四步Runge-Kutta方法。动网格技术采用弹簧近似方法实现,详细描述可参见文献[9]。

2 弹性敏感元件的运动方程

减压器运动机构包括主弹簧、副弹簧、阀芯(顶杆)、膜片,组成一个质量弹簧阻尼系统。图4为系统运动模型及参数定义示意图。

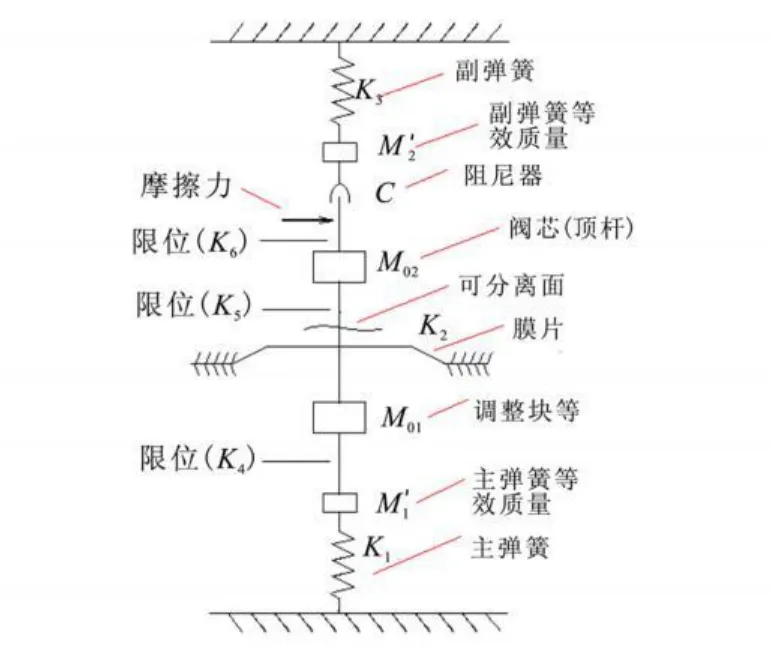
图4 弹性敏感元件运动模型Fig.4 Kinetic model of the elastic sensitive parts

鉴于系统运动的非保守性,运用拉格朗日方程来推导运动方程。根据减压器结构及运动特点,建立运动模型时考虑以下问题:

(1)由于膜片厚度很薄,当横向位移相对其较大时,需要考虑大位移效应(几何非线性)。为此将膜片看成非线性弹簧K2。采用有限元法计算主阀膜片位移变形与反力的关系。

(2)横向位移较大的情况下,膜片内部应力很大,可能超出其屈服限。因此,采用弹塑性模型来描述膜片的应力应变关系。

(3)安装有初始变形,在计算时考虑膜片预变形。(4)假设涨圈提供摩擦力恒定。

(5)为了完整描述系统动态运动过程,引入阻尼系数c来描述系统阻尼力。当考虑有摩擦力存在,阻尼力为次要地位,因此阻尼系数c很小(c=0.1)。

(6)阀芯(顶杆)与膜片调整块存在分离面,从分离面处将系统运动分为上下两部分,单独建模。

(7)阀芯与向下限位的撞击用非线性弹簧描述,即:接触→压缩→回弹→脱离,当脱离接触,不再有弹簧力。

(8)与膜片相连的调整块向上运动,当与阀芯顶杆接触后与其一起运动。当向下运动脱离接触,可继续运动,如果达到下限程,同样用非线性弹簧描述与下限位的碰撞。

取初始位置x2=0,向下运动L5=0.8741E-3(m)即到下限位。根据拉格朗日方程,可推导出上部分运动方程如式(14):

式中 L3=196/K3=3.94×10-3m为副弹簧预压缩量;f为摩擦力;Fq2为作用在阀芯上的气动力;FX为与下部接触力,当上下部分分离后,FX=0。

取初始位置x1=0向下运动L4=0.7×10-3+0.874 1×10-3=1.574 1×10-3m,即到下限位。根据拉格朗日方程,可推导出下部分运动方程如下:

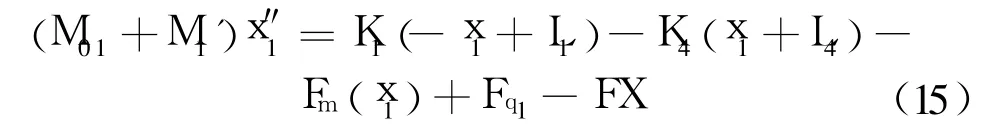
式中 L1=1 050/K1=10.38×10-3m,为主弹簧预压缩量;Fq1为作用在膜片上的气动力;FX为与上部接触力,当上下部分分离后,FX=0。

膜片上的气动力Fq1分为两部分:

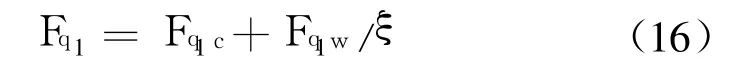
式中 Fq1c为φ＜25 mm范围的气动力;Fq1w为25mm＜φ＜35mm范围的气动力,折算系数ξ=2.12。

减压器弹簧-质量-阻尼系统的运动方程式(14)、式(15)是非线性的,采用纽马克方法求解。

3 计算结果与分析

计算网格采用非结构网格,几何建模基本接近真实设计外形。整个减压器表面网格见图5。减压器入口连接高压进气管路,高压气通过电磁阀进入进气管路,电磁阀开启时间从10～200ms不等。认为入口压力在电磁阀开启时间段内呈线性增大,电磁阀开启导致的快速增压过程使得进气管路中形成激波冲击。为了避免反射波向入口回传,干扰入口边界条件,本文采用一维流动模型入口出口边界条件。具体做法是在三维计算域的入口和出口处连接足够长的一维等截面管路数值模型,交界面上物理量的传递通过延拓2层网格单元实现。该方法示意见图5。

工作气体为空气,气体总温300 K。计算条件为上游高压气压力分别为21、15、8 MPa,电磁阀开启时间取20 ms和50 ms 2种情况。

图5 计算网格及出入口一维流边界条件Fig.5 Whole 3D model and 1D pipe flow boundary conditions in in let and outlet

图6是高压冲击某时刻的马赫数云图。图7为开启持续时间20 ms不同开启压力下高压腔和低压腔压力变化历程,图7中显示,开启压力为15MPa和8MPa下在稳定工作时高压腔和低压腔压力均没有振动而保持恒定值,开启压力为21 MPa时高压腔和低压腔压力均呈现出有限幅值的波动。计算得到的低压腔压力在1.7MPa左右。图8为开启压力21 MPa不同持续时间高压腔和低压腔压力变化历程。由图8可见,开启持续时间20 ms时高低压腔压力出现波动现象,而开启时间50ms时则没有波动,压力呈光滑变化,这说明延长电磁阀开启持续时间可减弱弹性元件的振动疲劳。图9为开启持续时间20 ms不同开启压力下的阀芯与膜片位移曲线,可见膜片硬芯与阀芯顶杆绝大多数时间都是结合在一起运动,只有开启压力大于15 MPa时在工作初期有短暂分离。开启压力为15 MPa和8 MPa且在稳定工作时阀芯开度稳定在各自的恒定值,开启压力为21 MPa时,则在较长时间内阀芯开度处于小幅振动状态。图10为开启压力21MPa、持续时间50ms的位移曲线,图10中显示,同样的开启压力,将持续时间延长到50 ms就能避免阀芯开度的振动,使开度稳定在恒定值。

图6 高压冲击某时刻的马赫数云图Fig.6 Transient Mach contours during the impact of high p ressure gas

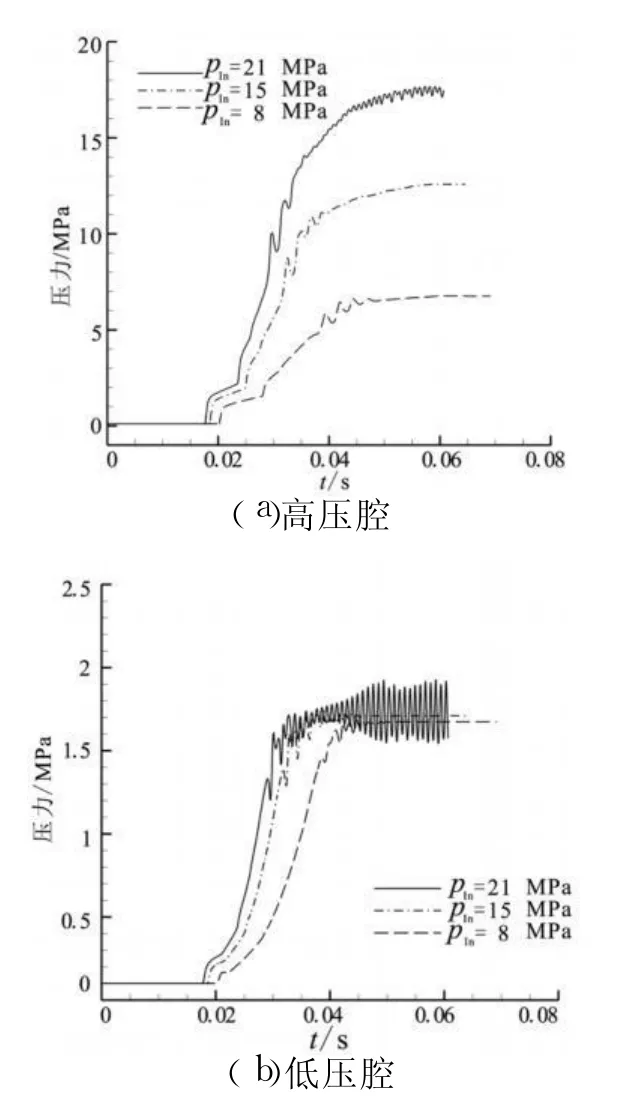
图7 不同开启压力下高低压腔压力变化历程对比Fig.7 History of p ressure in high and low p ressure room at different upstream p ressures

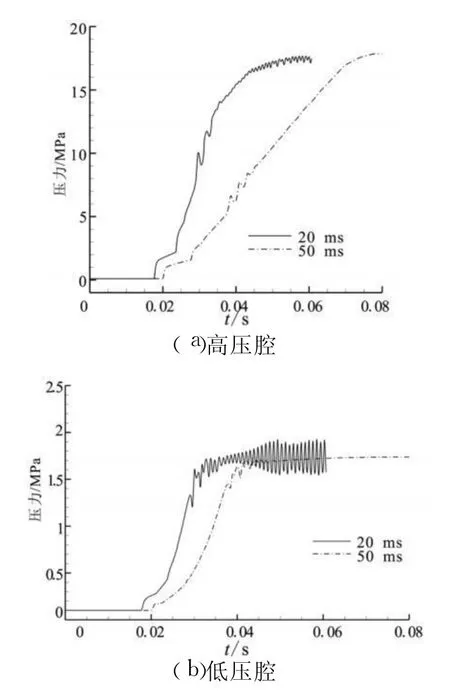
图8 入口21MPa不同持续时间高低压腔压力变化历程Fig.8 History of pressure in high and low pressure room at different upstream p ressurizing duration under 21MPa

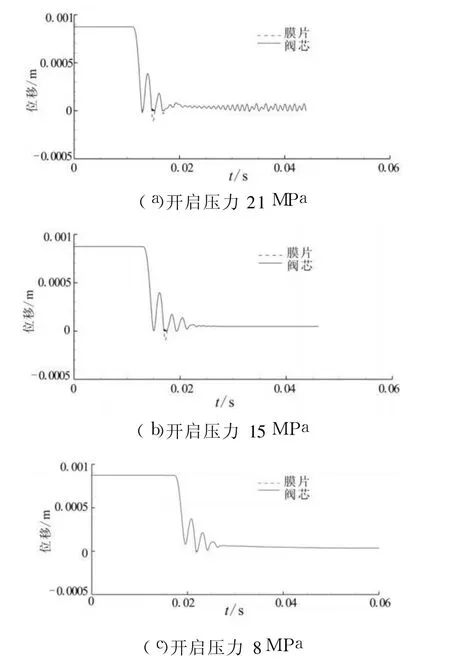
图9 不同开启压力下持续时间20m s阀芯与膜片位移Fig.9 Displacements ofmoving assembly at different upstream pressures and 20ms p ressurizing duration

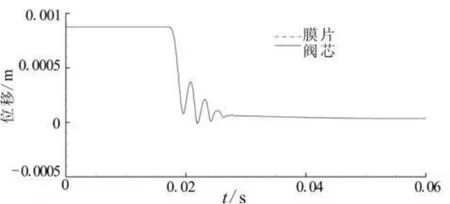
图10 开启压力21MPa持续时间50ms阀芯与膜片位移Fig.10 Displacements of moving assembly at 21M Pa upstream pressure and 50ms pressurizing duration

4 结束语

采用流固耦合数值模拟技术研究了减压器工作过程的动态特性,得到了减压器在不同上游压力和不同开启时间条件下弹性敏感元件的运动规律。结果表明,开启压力为21 MPa时,如果开启持续时间为20 ms,则高压腔和低压腔压力以及弹性元件的运动均呈现出有限幅值的波动;而开启时间50 ms时则没有波动,压力呈光滑变化趋势,阀芯开度稳定在恒定值。这说明延长电磁阀开启持续时间可减弱弹性元件的振动疲劳。

本文提出的虚拟挡板技术成功模拟了活门由闭到开的瞬态过程,表明该技术模拟物体间由零距离开始分离的实际过程是成功的,且对最小网格尺度没有限制。

[1] Fejtek I,Waller G,Wong R.Computational study of the flowfield of an aircraft outflow valve[R].AIAA 2005-4843.

[2] Ahuja V,Hosangadi A,Shipman J,etal.Simulations of instabilities in com plex valve and feed systems[R].AIAA 2006-4758.

[3] Cavallo P A,Hosangadi A,Ahuja V.Transient simulations of valvemotion in cryogenic systems[R].AIAA 2005-5152.

[4] 徐克鹏,蔡虎,崔永强,等.大型汽轮机主汽调节阀的实验与数值分析[J].动力工程,2003,23(6):2785-2789.

[5] 王冬梅,陶正良,贾青,等.高压蒸汽阀门内流场的二维数值模拟及流动特性分析[J].动力工程,2004,24(5):690-697.

[6] 樊希葆,谢水波,陈泽昂,等.水泵站停泵水锤数值计算理论研究——模型求解与应用[J].南华大学学报(自然科学版),2005,19(2):6-9.

[7] 聂万胜,陈新华,戴德海,等.姿控推进系统发动机关机的管路瞬变特性[J].推进技术,2003,24(1):6-8.

[8] Barth T J,Jespersen DC.The design and application of upwind schemes on unstructured meshes[R].AIAA 89-0366.

[9] 郭正.包含运动边界的多体非定常流场数值模拟方法研究[D].长沙:国防科技大学,2002.