一种对称损失下Burr分布参数的Bayes估计

刘 冰

(吉林师范大学 数学学院，吉林 四平136000)

Burr分布是由BurrI.W.在1942年首先引入的，如今在社会科学、经济科学、环境科学、保险精算学等诸多领域内得到了广泛应用.特别地该分布还被列入了精算师常用八大分布之一，可见其在应用中的重要性.张彩平[1]在经典统计的前提下研究了三参数Burr分布的估计和检验问题.陈志强等[2]研究了熵损失函数下Burr分布参数的Bayes估计，本文将讨论在一种对称损失下，当参数α已知时，Burr分布参数θ的Bayes估计.

双参数Burr分布的随机变量，其密度函数是

f(x|θ，α)=θ·α·xα-1·(1+xα)-(1+θ),

x>0,θ>0,α>0

(1)

我们在对称损失函数[3]

(2)

意义下考虑参数θ的估计，其中δ是θ的判决空间的一个估计，可知这个损失函数关于δ是严凸的，且在δ=θ处取得唯一的最小值.

1 参数θ的Bayes估计

我们讨论参数θ的Bayes估计，记X=(X1,X2,…,Xn)，对任意先验分布π(θ)，θ的Bayes估计均为

取先验分布为Burr分布参数θ的共轭先验分布Gamma分布Γ(α,λ)，其密度函数为

(3)

其中m，λ，θ为未知参数.下面以定理形式给出给定先验分布后参数θ的Bayes估计的精确形式.

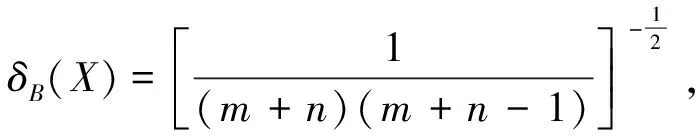
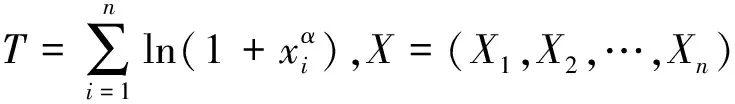
2 参数的多层Bayes估计

在共轭分布(3)中m,λ是未知参数，那么δB(X)中仍然含有超参数m,λ，因而需要进一步讨论θ的多层Bayes估计.文献[4]介绍了选择多层先验分布的原则和方法，由Burr分布的特征，采用减函数法来确定超参数m,λ的先验分布.

π2(m)=U(0,1),π2(λ)=U(0,c)，c为常数.

(4)

定理3 对于Burr分布取(3)和(4)为θ的先验分布,在损失(2)下，θ的多层Bayes估计为

证明 由(3)和(4)可知，θ的先验分布为

从而θ的后验密度函数为

则在损失(2)下，θ的多层Bayes估计为

3 Bayes估计的容许性

定理4[5]在给定的Bayes决策问题中，假如对给定的先验分布π(θ)的Bayes估计δB(x)是唯一的，则它是容许的.

证明 假设δB(X)是非容许的，则存在另一个估计δ(X)≠δB(X)，使得R(θ,δ)≤R(θ,δB)，∀θ∈Θ且至少对某一个θ有严格不等式成立，上式两边对先验分布积分，可知δ(X)是θ的Bayes估计，这与唯一性矛盾，故δB(X)是可容许的.

从这个定理可以看出，当损失函数是严格凸函数时其Bayes估计必是唯一的，从而也是可容许的.由对称损失函数(2)是关于δ的严格凸函数，则其Bayes估计必是唯一的，由定理4可知，δB(X)是可容许的.

参考文献:

[1]张彩平.三参Burr分布的估计和检验问题[D].上海:华东师范大学,2006.

[2]陈志强,韦程东,程艳琴.熵函数Burr分布参数的Bayes估计[J].广西师范学院学报,2007,24(3):30-34.

[3]徐宝.一种对称损失下Poisson分布参数倒数的Bayes估计[J].吉林师范大学学报,2006(3):53-54.

[4]韩明.多层先验分布的构造及其应用[J].运筹学与管理,1997,6(3):31-40.

[5]茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.363-368.