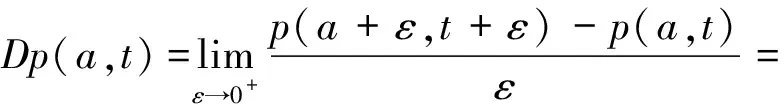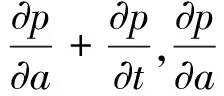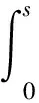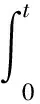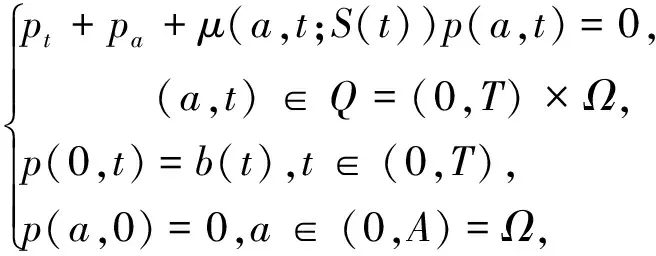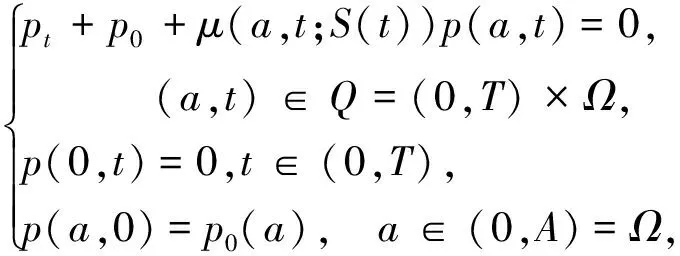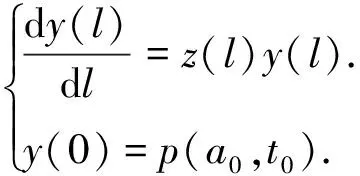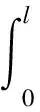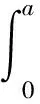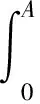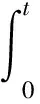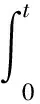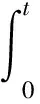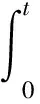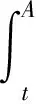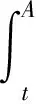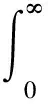一类具有年龄和加权的半线性种群系统的解

代丽丽,宋芳芳

(通化师范学院 数学系,吉林 通化134002)

1 问题的陈述

本文考虑与年龄相关的半线性时变种群系统(P)：

其中p(a,t)是时刻t年龄为a的单种群年龄密度分布,p0(a)是t=0时种群年龄密度的初始分布,Q=(0,A)×(0,T),T是某个固定时刻,0

2 系统解的表达式

定义1 所谓系统(P)的解是指函数p(a,t)∈L∞(Q)沿着t-a=C(C为常数)绝对连续,且满足

定理1 固定函数S∈L∞(0,T),S(t)≥0对于任意的t∈(0,T),应用特征线法可将系统(P)的解表示为

(1)

其中

s∈(0,min{a,t}).而b(·;S)为下列Volterra积分方程的解

t∈(0,T)

(2)

这里

F(t;S)=

(3)

K(t,a;S)=β(a,t;S)∏(a,t,a;S)

证明 固定函数S∈L∞(0,T)，S(t)≥0，∀t∈(0,T)，为求解下列方程组

(4)

我们将其分解为两个方程组(Ⅰ)和(Ⅱ)：

(5)

(6)

第一步：解方程组(5).

由一阶偏微分方程的有关理论知，与(5)中的第一式完全等价的常微分方程组为

(7)

由(5)中的第二式所表示的边界条件可用如下用参数τ的方程表示

a0=0，t0=τ，p(0,τ)=b(τ).

(8)

将(7)的前两个方程的解代入(7)的第三个方程中，有

-μ(a0+l,t0+l;S(t0+l))p(a0+l,t0+l).

(9)

为表示方便，令y(l)=p(a0+l,t0+l),

z(l)=-μ(a0+l,t0+l;S(t0+l))，于是有

p(l,τ+l)=p(0,τ)exp{-

对任意t>a>0，得

p(a,t)=b(t-a)exp{-

此解显然满足边界条件p(0,t)=b(t)，将b(t)在(-∞,0)上延拓为0，则方程组(5)的解有表达式

(10)

第二步：用同样的方法解方程组(6).

方程组(6)的解有表达式为

(11)

由(10)和(11)不难看出，在区域G={(a,t)|a≥0,t≥0}上，方程组(4)的解可表示为

(12)

其中

(13)

第三步：将系统(P)的解(12)表示为(1)的形式.

为了将系统(P)的解表示为(1)的形式，我们作如下变换：当a>t>0时，令ρ=t-τ，则

(14)

当a≤t时，令ρ=a-τ，则

(15)

由(14)、(15)，令

∏(a,t,s;S)=

s∈(0,min{a,t})

(16)

将(16)代入(12)，则

(17)

将解的表达式(17)代入(13)，有

其中K(t,a;S)=β(a,t;S(t))∏(a,t,a;S)

t)∏(a,t,t;S)da+u(t)

(18)

作变量替换，令a=l+t，则上式中

(19)

F(t;S)=

证毕.

参考文献:

[1]于景元,郭宝珠,朱广田.人口分布参数系统控制理论[M].武汉:华中理工大学出版社,1999.

[2]陈任昭,李健全.非线性时变种群系统解的存在唯一性[J].数学物理学报,2003,23(2):1-17.

[3]陈任昭.关于人口发展过程的偏微分方程非齐次边值问题[J].东北师范大学学报,1982(2).

[4]Barbu V and Iannelli M. Optimal Control of Population Dynamics[J].J.Opti.Theo.Appl.1999,102(1):1-14.

[5]Anita S.Optimal Harvesting for a Nonlinear Age-dependent Population Dynamics[J].J.Math.Anal.Appp.,1998,226:6-22.