最小控制合成算法在结构振动控制中的应用

张凯静， 周莉萍， 王官磊

(1.中南建筑设计院股份有限公司， 湖北 武汉 430070； 2.武汉市人防建筑设计研究院， 湖北 武汉 430022；3. 长江航道规划设计研究院， 湖北 武汉 430011)

近年来大规模地震不断发生，2008年汶川地震，2009年印尼地震都给人类带来巨大生命财产损失。传统的结构设计主要依靠提高结构自身刚度和抗侧移能力来抵抗重型机器荷载、暴风、强地震等动力作用。结构振动控制可以有效地减轻结构在风和地震等动力作用下的反应和损伤，有效提高结构抗震能力和抗灾性能。

结构振动控制是近年来兴起的工程结构抗震的新途径，其中主动控制、半主动控制和智能控制技术因控制效果好，控制过程智能可调等优点而被许多结构工程专家所关注，并且正在获得越来越多的工程应用[1]。

结构振动的控制技术中，要获得较好的控制效果，关键是要采用合适的控制算法和控制策略。目前，国际和国内提出了多种控制算法和策略，但是多数控制算法由于需要精确的结构参数模型而很难在实际的复杂结构中应用。并且，多数控制算法必须通过反复的参数优化调节来使结构振动响应趋于减小，而不能根据需要预先确定好控制结构的响应[2]。因此，发展不依赖受控结构参数模型的控制算法和控制策略是十分必要的。

本文基于“最小控制合成算法(MCS)”的自适应控制理论，推导了地震反应自适应控制的基本方程。提出了以地震能量降低模型为最优控制模型，应用以地震能量降低模型的MCS控制算法，对一个三自由度受控结构和天兴洲大桥磁流变阻尼器进行仿真分析。

1 MCS参考模型自适应控制算法

1990年Stoten和Benchoubane 等[3～7]提出了最小控制合成算法(MCS)，最小控制合成算法是在模型参考自适应控制算法下的改进，但又不同于模型参考自适应控制，因为除了自由度和系统状态的维数外，它不需要预先知道被控动力系统的任何参数信息。MCS算法在系统参数变化、外部干扰、系统内部动力耦合与系统非线性的情况下均能达到良好的稳定性和鲁棒性。图1表示了MCS控制算法的结构。

n个自由度的结构在环境干扰F(t)作用下，通过控制装置提供控制力U(t)后，受控结构的运动方程可以表示为[8]：

(1)

式中，X∈Rn为结构的位移向量;M、C和K∈Rn×n是结构的质量、阻尼和刚度矩阵；Ds∈Rn×r是环境干扰位置矩阵;Bs是结构提供控制力U(t)相对应的位置矩阵。

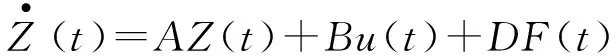
(2)

参考模型的状态方程为：

(3)

Am和Bm与结构的自振特性有关，可以用结构的自振频率ωn来表示；

在方程(1)中，整个系统被认为是一个多自由度子系统，该子系统仅包含一个或两个输入，其最小控制合成算法原理如下：

u(t)=K(t)Z(t)+Kr(t)r(t)

(4)

式中，r(t)是输入，K(t)，Kr(t)是自适应增益，由下面的方程确定：

(5)

其中，α、β为正的加权数值，初始条件通常设为0；标量α和β决定了自适应控制效果，通常凭经验选取。

模型信号误差：

Ze(t)=Zm(t)-Z(t)

(6)

其中，Zm(t)是参考模型的输出响应，Z(t)是被控结构的输出响应。

ye(t)为系统的输出误差信号，可表示为：

ye(t)=CeZe(t)

(7)

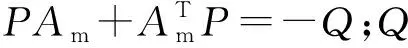
(8)

2 基于MCS算法的仿真分析

2.1 降低地震能量参考模型

地震通常是以能量的形式对结构造成破坏，结构吸收的地震能量越多，受到破坏也就越深。地震过程中，单质点弹性体系所消耗的单位质点的能量可以表示为：

(9)

式中，I为结构所消耗的能量，Td为震动的持续时间，a(t)是地震加速度。由上式可以知道，地震能量与地震加速度密切相关。因此，采用某种策略减小地震速度，以减小后的地震加速度输入到结构中得到的振动响应作为参考模型，运用MCS最小控制合成算法就能计算控制力，将该控制力作用在结构上便能有效降低结构吸收的地震能量，保证结构的安全。

2.2 基于MCS算法的主动控制

用MATLAB建立一个三层剪切型框架结构模型，该框架每层质量为m=4×105kg，刚度为k=2×108N/m，结构阻尼采用Rayleigh阻尼，由前二阶振型阻尼比确定，即C=αcM+βcK=0.7355M+0.002643K。地震波激励为El-Centro波，激励的持续时间50 s，地震输入峰值为200 Gal。

在抗震设防烈度为8度时，地震设计基本地震加速度峰值为0.2g。以抗震设防烈度为7度时的加速度峰值0.1g作为输入，得到的结构振动响应作为参考模型，通过MCS自适应控制算法计算出控制力并输入到结构中。这样，结构在抗震设防烈度为8度时，仅吸收了相当于7度时的地震能量，其它能量被控制装置所吸收。

图2 第一层参考模型地震响应与被控结构地震响应的比较

图3 第二层参考模型地震响应与被控结构地震响应的比较

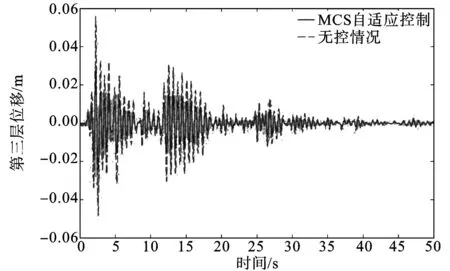
图4 第三层参考模型地震响应与被控结构地震响应的比较

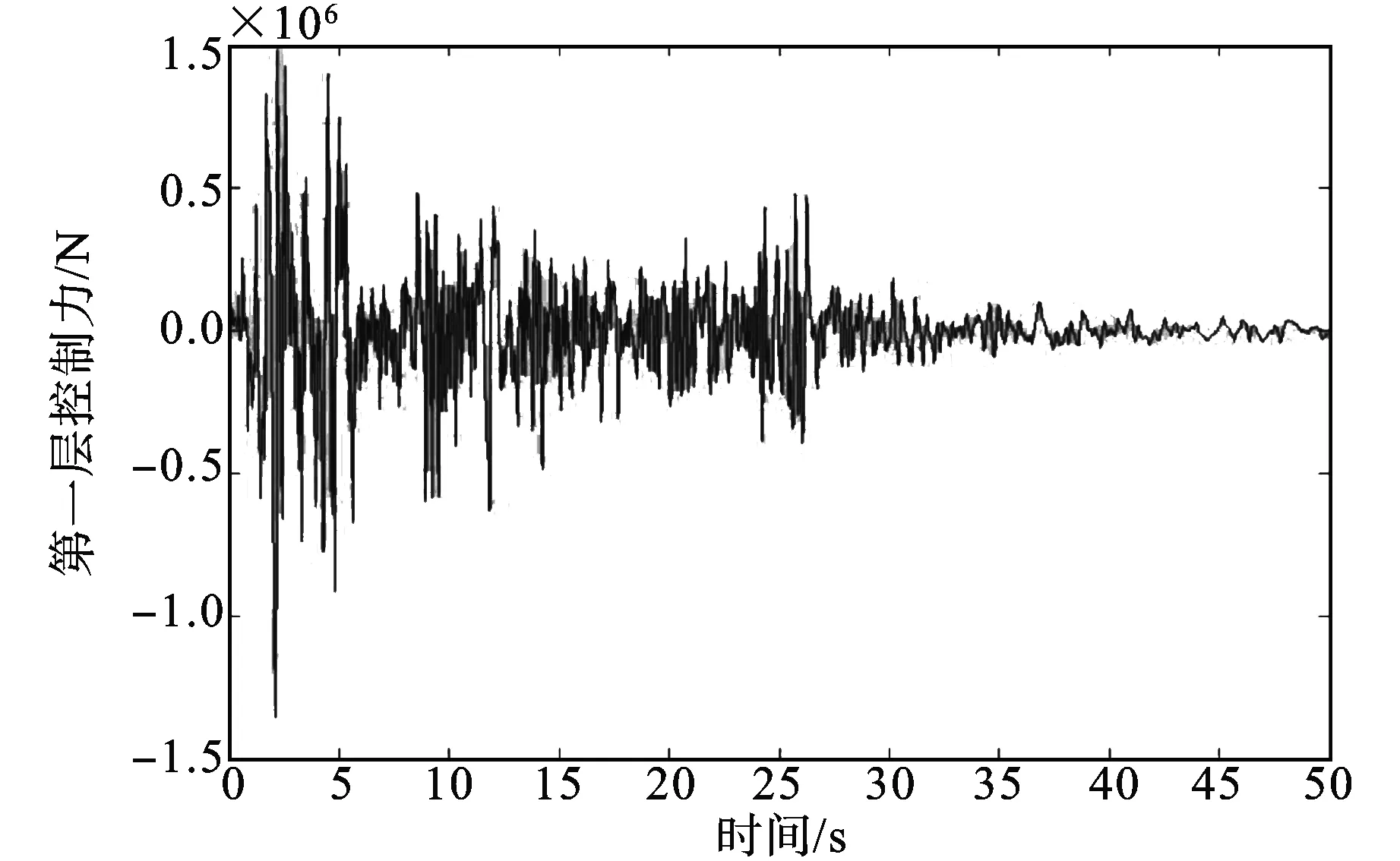
图5 第一层控制力

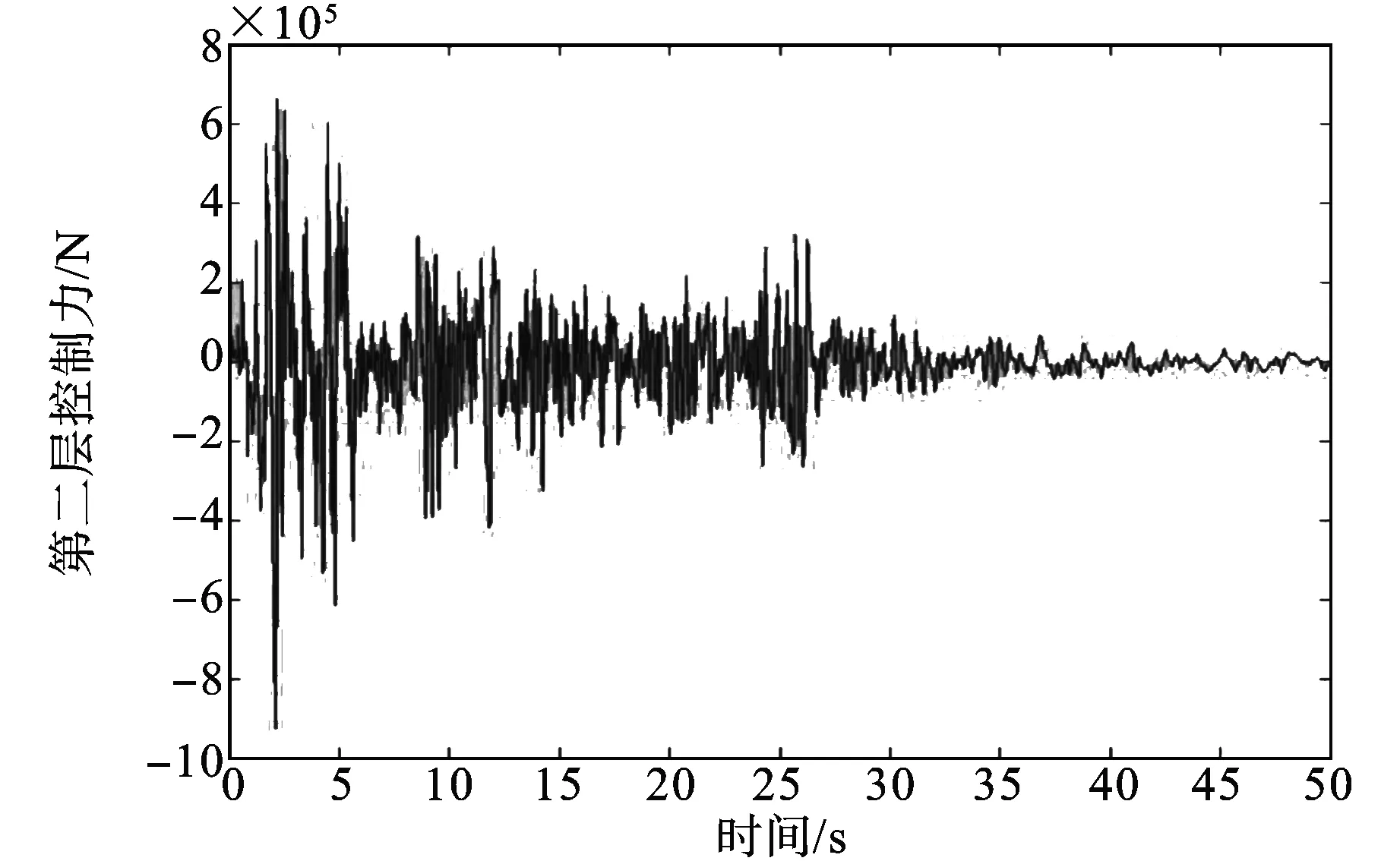
图6 第二层控制力

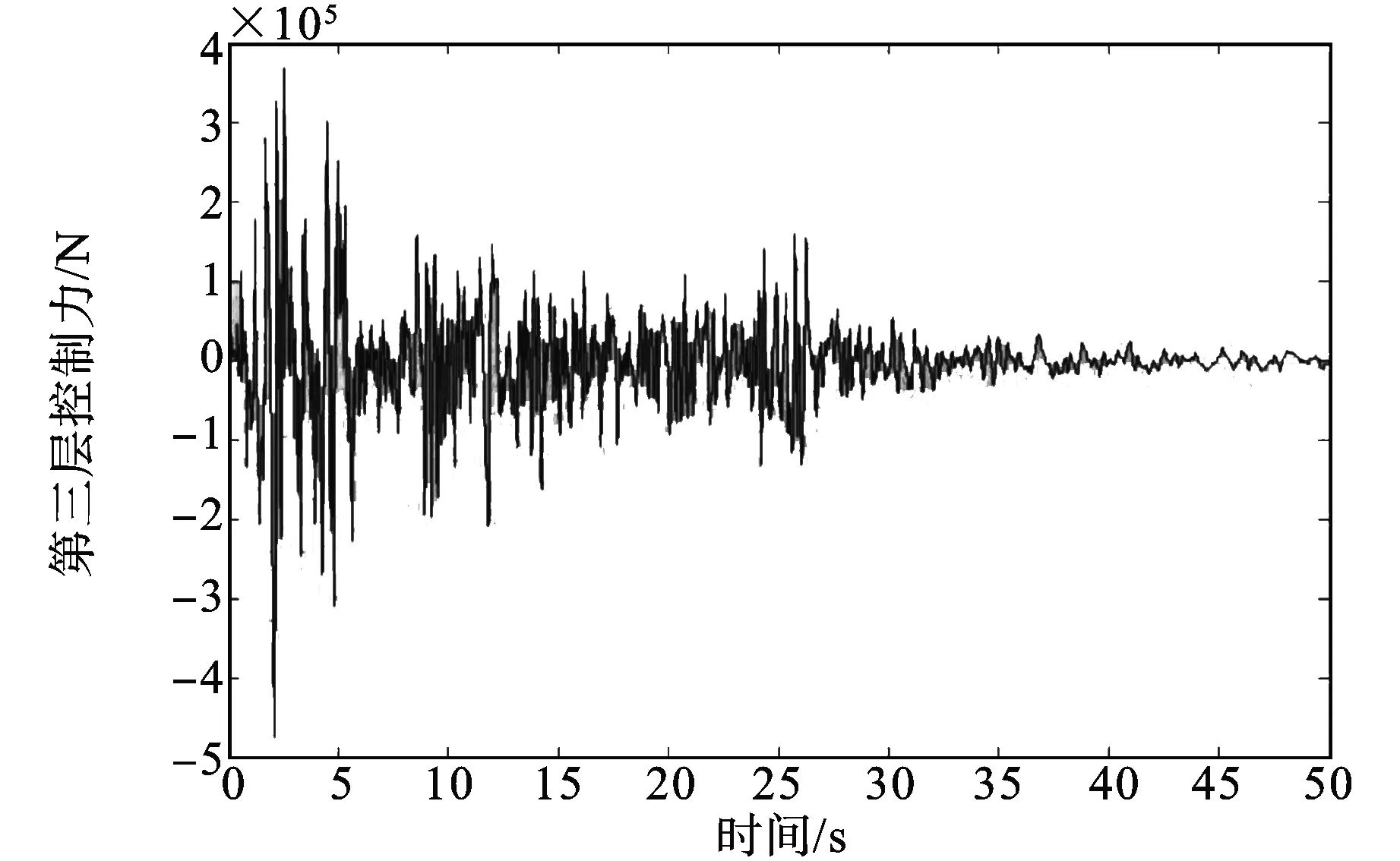
图7 第三层控制力

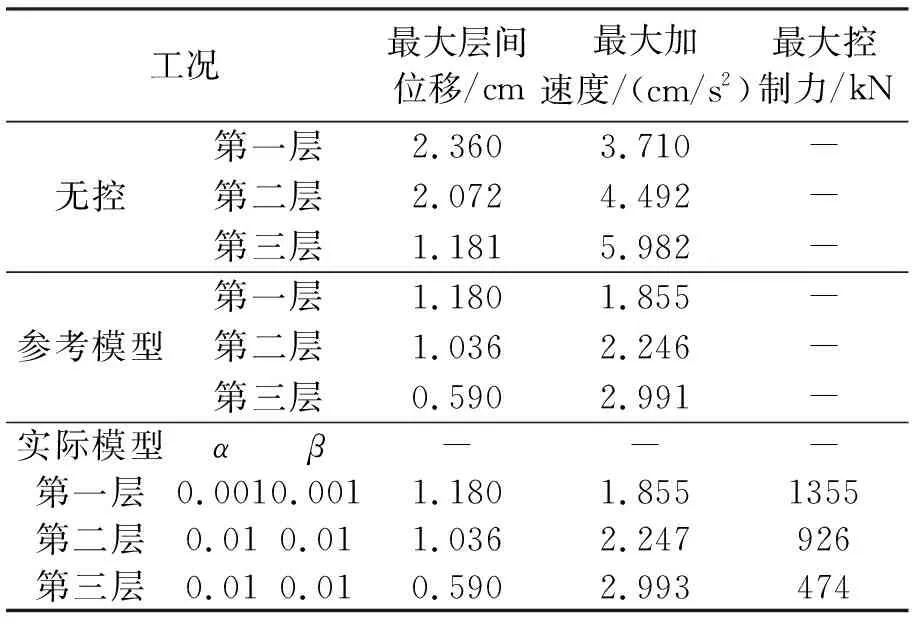
表1 结构地震最大反应和控制力(降低地震为参考模型)

对于多自由度模型，以地震能量降低模型作为参考模型，MCS控制算法可以计算出减小结构响应和加速度响应的控制力，图2～7显示了受控和无控情况下结构各层的位移响应和控制力时程。从表1中可以看出，第一层的位移响应从2.360 cm减小到1.180 cm，第二层的位移响应从2.072 cm减小到1.036 cm，第三层的位移响应从1.181 cm减小到0.590 cm，位移都减小了50%。

2.3 基于MCS算法的半主动控制

以天兴洲大桥上某个磁流变阻尼器作为研究对象[9]，阻尼器输出力为20～500 kN，利用修正的Bingham模型模拟磁流变阻尼器，采用基于Sigmoid函数模糊控制策略，外部干扰为El-Centro地震波，激励的持续时间100 s，地震输入的峰值为100 Gal。

图8～9显示了天兴洲大桥主梁在受控和无控制情况下的位移响应时程，主梁纵向地震位移在无控情况下最大值为0.214 m，装上了磁流变阻尼器后，即使在不通电的情况下，位移的幅值降为了0.149 m，此时最大位移相当于下降了30%；当磁流变阻尼器通上了0～1A的电流开始工作，结构的位移响应从最大值0.214 m下降至控制后的0.077 m，下降幅度达到了64%，图10显示了MCS算法计算出来的控制力时程，利用MCS算法计算出来的控制力最大达到了452.2 kN，图11显示了磁流变阻尼器理论上输出的控制力时程，磁流变阻尼器作为半主动控制装置计算产生的最大阻尼力为393.9 kN，显然磁流变阻尼器能对天兴洲大桥主梁的纵向地震反应具有很好的抑制效果，保证了天兴洲大桥正常的使用和安全[10]。

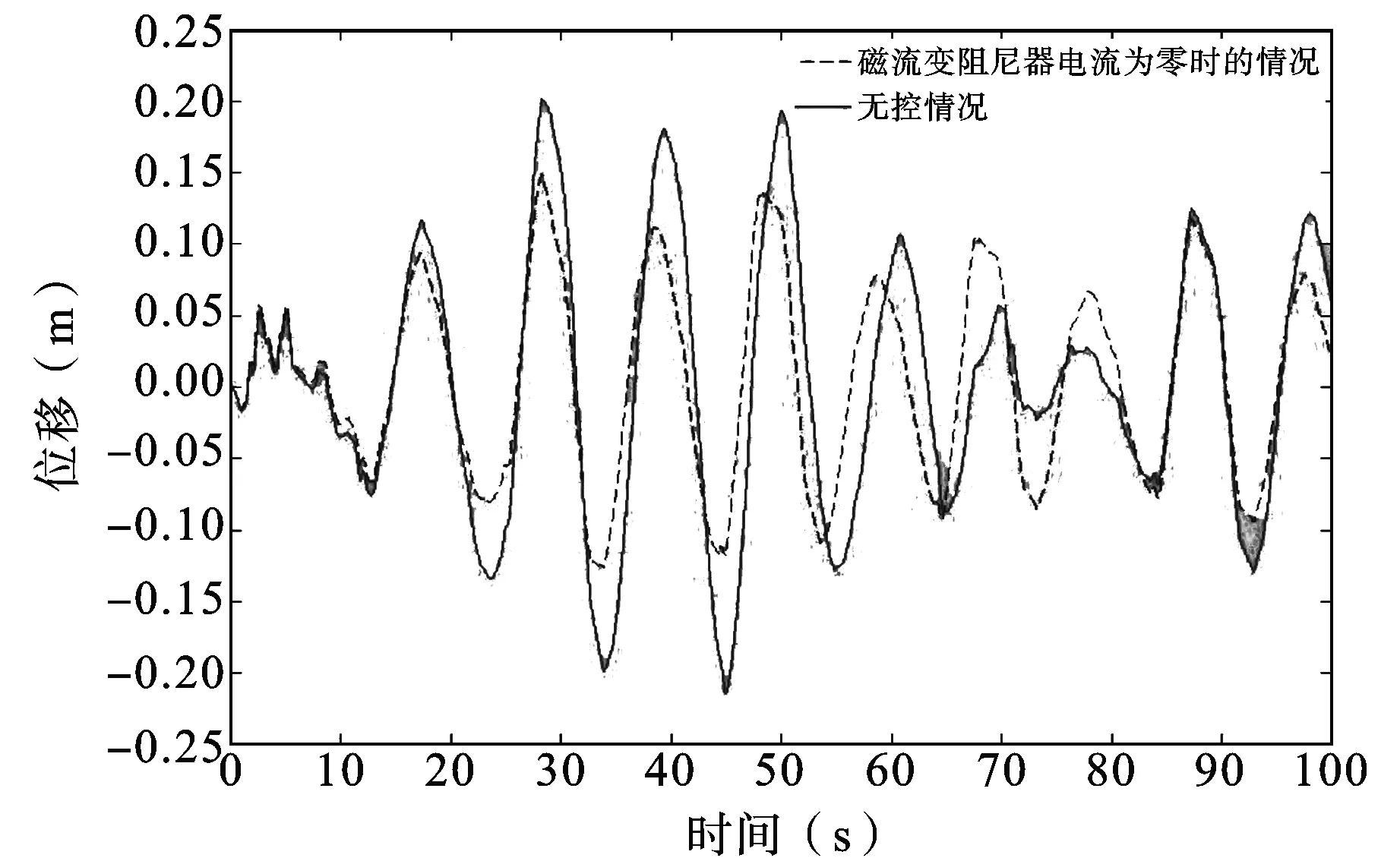
图8 主梁纵向振动位移时程曲线(无电)

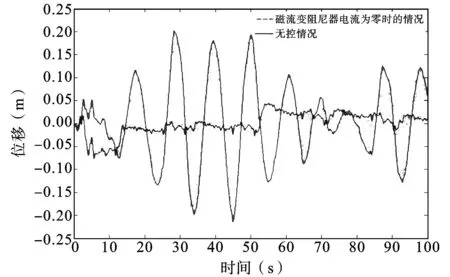
图9 主梁纵向振动位移时程曲线(有电)

图10 阻尼器控制力时程曲线

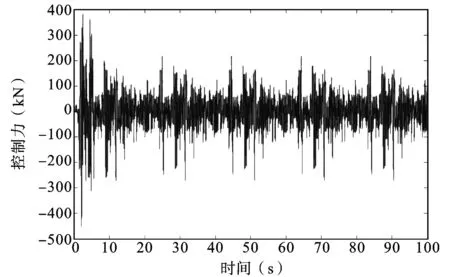
图11 MCS算法控制力时程曲线

3 结 论

本文将基于参考模型的最小控制合成算法引入结构振动控制中，提出了以降低地震能量为参考模型，并对基于降低地震能量为参考模型的MCS控制算法进行了仿真分析。仿真结果表明：

(1)MCS控制算法除了自由度和系统状态的维数外，不需要被控对象动力特性的任何数值信息。

(2)MCS控制算法能够使结构动力响应精确跟踪参考模型，从而可以定量地达到自己设定的控制效果。

(3)天兴洲大桥是漂浮型的公铁两用斜拉桥，其主梁会因纵向地震引起较大的纵向振动位移反应，将会影响大桥的正常使用和安全，必须用纵向设置的阻尼器来抑制它。

[1] 胡寿松. 自动控制原理(第4版)[M]. 北京: 科学出版社, 2001.

[2] Soong T T.Active Structural Control:Theory And Prac-tice[M]. NewYork: John Wiley & Sons, Inc., 1990.

[3] Stoten D P, Gomez E G. Adaptive control of shaking tables using the minimal control synthesis algorithm [J]. Phil. Trans. R. Soc. Lond. A, 2001, 359(1786): 1697-1723.

[4] Wagg D J,Stoten D P.Substructuring of dynamical sys-tems via the adaptive minimal control synthesis algorithm [J]. Earthquake Engineering and Structural Dynamics, 2001, 30(6): 865-877.

[5] Koganezawa K, Stoten D P. Adaptive control of manipulators via an extension to the error-based minimal control synthesis with integral action algorithm[C]//2007 IEEE International Conference on Robotic and Automation, 2007:1960-1967.

[6] Stoten D P, Benchoubane H. The minimal control synthesis identification algorithm[J]. International Journal of Control, 1993, 58(3): 685-696.

[7] Lim C N, Neild S A, Stoten D P, et al. Adaptive control strategy for dynamic substructuring tests[J]. Journal of Engineering Mechanics, 2007, 133(8):864-873.

[8] 欧进萍.结构振动控制——主动、半主动和智能控制[M].北京：科学出版社，2003.

[9] 周 强, 瞿伟廉. 磁流变阻尼器的两种力学模型和试验验证[J]. 地震工程与工程振动, 2002, 22(4): 144-150.

[10] 瞿伟廉, 刘 嘉. 天兴洲大桥主梁纵向地震反应的被动控制[J]. 武汉理工大学学报, 2007, 29 (1): 128-131.