行车荷载作用下沥青路面的动粘弹性分析
2010-01-25朱东辉
朱东辉
(平顶山市公路管理局, 河南 平顶山 467000)
国内外现行的路面设计方法一般基于静态弹性体系模型,而实际车轮荷载为动态,由于路面结构本身对荷载的时变因素具有相当的敏感性,因而在动载作用下所表现出的力学性能通常与静态模型的情况存在较大差异。
国内外学者从20世纪70年代开始对路面结构动态力学模型进行研究。Gillespie[1]为研究重载车辆对路面的破坏作用,对动荷载特征和路面响应进行研究,分析了轴载、车辆悬挂系统、轴距、轮压等因素的影响;Uddin[2]采用三维有限元模型,模拟FWD作用于沥青路面表面,分析了荷载大小、加载时间等因素对路表弯沉的影响;Zaghloul和White[3]考虑了路面沥青材料的粘弹属性,并进行了敏感性分析。但是,这些文献中施加的荷载的位置都是固定不变的,与路面上车辆行驶的实际情况不符。基于此,利用有限元数值分析方法,对多层沥青路面在移动荷载作用下的响应进行了分析。
1 行车荷载下的沥青路面有限元模型
1.1 模型假设
(1) 沥青面层为粘弹性材料,半刚性基层均为线弹性,土层采用D-P模型参数;
(2) 沥青面层与半刚性基层间考虑其接触状态,其它各层均为完全联接;
(3) 计算模型简化为轴对称模型;
(4) 考虑阻尼并且采用瑞利阻尼,采用等效荷载,不考虑自重应力场作用。
1.2 沥青路面的结构模型
建立ANSYS内的数值分析模型。该分析模型分为四层,分别为沥青面层、基层、底基层以及土层。分析中路面材料结构参数见表1。土基的D-P模型中,粘聚力c=75.4 kPa,摩擦角φ=11.2°。对沥青路面材料,采用广义Maxwell模型来描述沥青混合料的松弛性能。对于N个Maxwell体并联组成的广义模型,其应力松弛模量(MPa)为
(1)
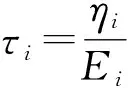

表1 路面材料结构参数

表2 面层材料的广义Maxwell模型的模型参数[4]
1.3 加载方式
荷载采用规范的双轮垂直荷载[5],接地形状采用矩形18.9 cm×18.9 cm。荷载沿着图1中阴影移动,模拟车辆行驶过程,荷载形式采用循环荷载,模拟车轮行走,等效速度为120 km/h;温度为绝对温度293 K,即室温20℃。
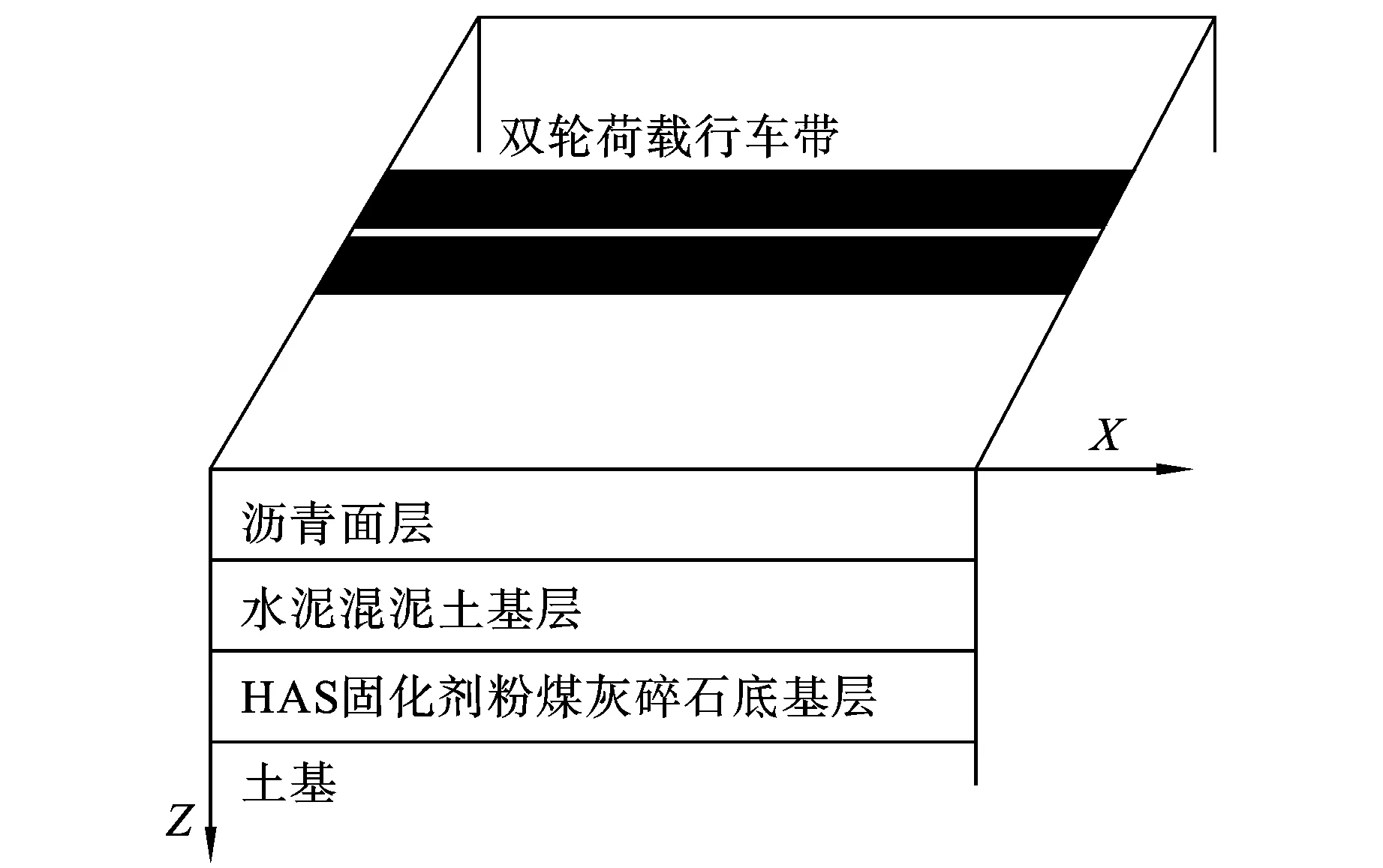
图1 路面分析模型
1.4 层间接触状态
ANSYS的接触问题需要定义接触刚度,两个表面之间渗透量的大小取决于接触刚度,过大的接触刚度可能会引起总刚矩阵的病态,而造成收敛困难。一般来说,应该选取足够大的接触刚度以保证接触渗透小到可以接受,但同时又应该使接触刚度不会引起总刚矩阵的病态问题而保证收敛性。通过试算不同数量级的接触刚度,得到竖向位移与接触刚度的关系曲线,如图2所示。
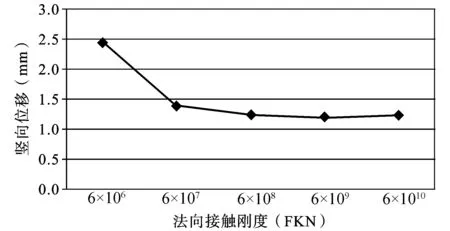
图2 竖向位移与FKN的关系曲线
由图2可以看出,当法向接触刚度达到108量级时,位移趋于稳定,考虑到模型的收敛性,将FKN取为6×108。将FTOLN取为0.08,此值与FKN的取值相协调,能很好地满足模型的收敛性和接触关系。
2 有限元结果分析
首先,我们对模型进行模态分析,得到模型的第一自振频率为18.72 Hz,竖向振动。ζ1取0.05,计算出瑞利阻尼系数α=5.881,β=4.25×10-4。将α和β值代入模型,采用小位移瞬态分析求解,算出结果。
2.1 接触状态的影响
在ANSYS中,进入POST1分析处理器,对结果进行一般性的分析。图3、图4分别为部分接触沥青层竖向位移云图和完全接触沥青层竖向位移云图。

图3 部分接触竖向位移云图

图4 完全接触竖向位移云图
2.1.1竖向变形对比分析
从图3和图4中可以看出:(1)该模型是位移连续的,这一点不难理解,该模型共划分了三万个单元,对于一般性数值模拟已经具有相当高的精度;(2)由于车辆荷载是自左向右开行的,从云图中可以明显看出,又因为表层沥青层是粘弹性材料,故云图中出现向左的尾巴;(3)该云图让我们更深入理解了粘弹性材料的性质,即卸载后随时间具有恢复性,但不是瞬时恢复;(4)加载和卸载点的存在导致了前端和后端的变形异样性。
对比分析图3和图4,部分接触的竖向最大残余变形为0.142 mm,而完全接触只有0.115 mm,说明较部分接触,完全接触对竖向变形有着更大的抵抗作用。
2.1.2x向应力对比分析
对比分析图5和图6,部分接触的x向残余拉应力为0.35 MPa,而完全接触只有0.14 MPa,说明较部分接触,完全接触能明显降低x向拉应力。

图5 部分接触x向应力云图

图6 完全接触x向应力云图
2.1.3剪应力对比分析
对比分析图7和图8,部分接触的xy向残余剪应力为0.18MPa,而完全接触只有0.17MPa,说明较部分接触,完全接触能稍微降低xy向剪应力,但远不如对x向拉应力的影响明显。
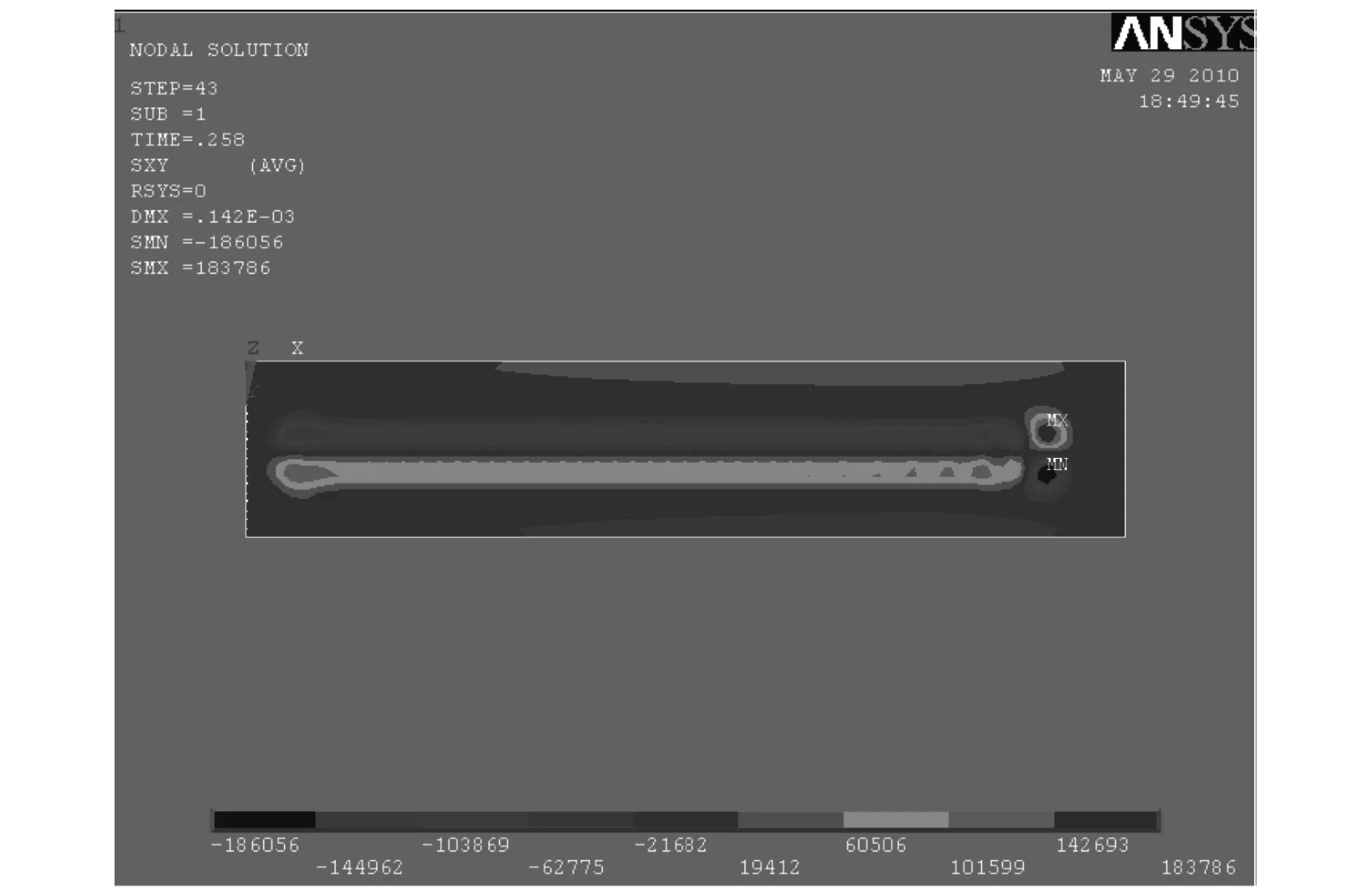
图7 部分接触xy向剪应力云图
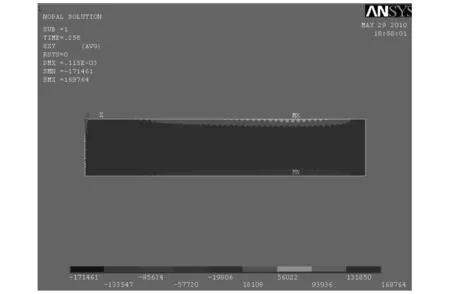
图8 完全接触xy向剪应力云图
综上所述,完全接触比部分接触更为优越,特别是对x向拉应力的降低作用尤为显著。完全接触的路面具有更好的变形连续和协调性,不会出现分层,大大减小表面沥青层的弯拉应力。
然而,完全接触只是一个理想状态,在现实生活中,路面接触都为部分接触。但是,从分析中可以明显看出,接触程度越高,路面的竖向变形越小,x向拉应力越小,xy向剪应力越小。
2.2 荷载作用下的路面响应特征
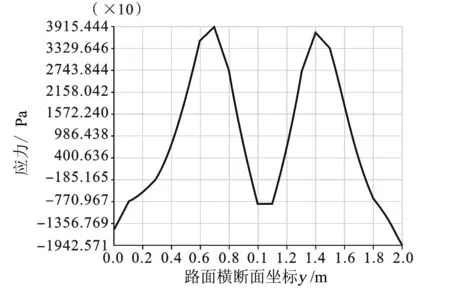
图9 表层x=4 m处x向应力
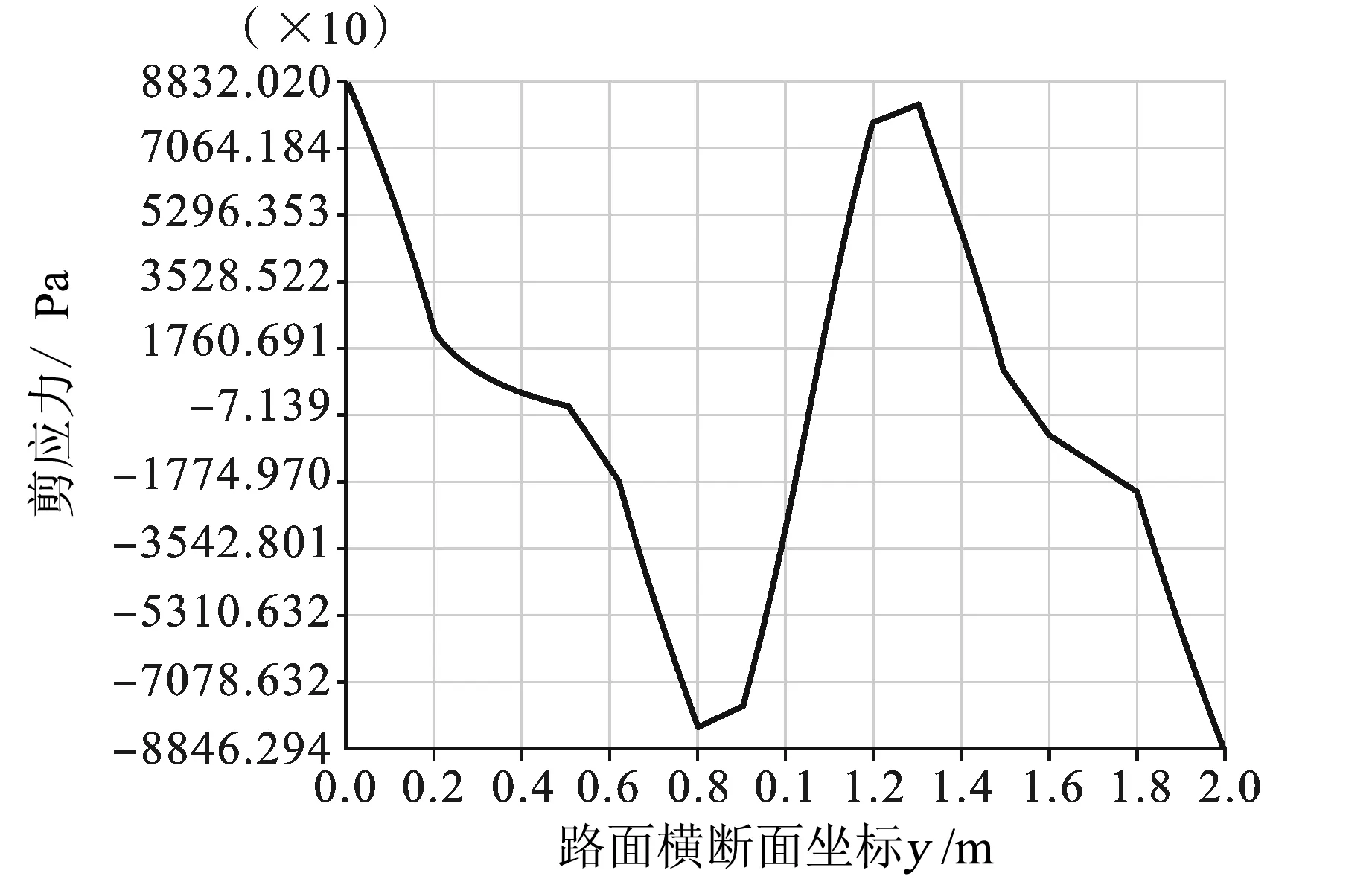
图10 表层x=4 m处xy向剪应力

图11 表层x=4 m处竖向位移
层间部分接触的结果见图9~图11。 图9中x向正应力对称分布和图10中xy向剪应力反对称分布,可以用结构力学中简单力学知识给予定性分析。该路面模型是对称结构,加载面处于对称轴上,即为对称荷载,所以,正应力对称分布,剪应力反对称分布。图11中,可以明显看出,荷载作用处残余变形仍然是最大的。相应地,加载点两侧相对而言位移较小;产生伪隆起的原因就是沥青材料的“剪切变稀”特性。在正常的行车荷载作用下,沥青的粘度随剪应力或剪切速率增加而减小,这说明离车轮越远粘度越大。当车轮荷载向下及向两边推挤沥青路面时,由于车轮四周沥青粘度比车轮底部高,因此难以向两边推挤形成车辙,而更倾向于形成车轮两边的拥包变形。
2.3 节点时间历程响应分析
表层x=4 m某一节点的时间历程响应曲线如图12~图14所示。可以看出,竖向位移、x向应力以及xy向剪应力的时间历程都出现了峰值,且峰值所在位置即为荷载到达该点的时间,与实际相符合。观察每幅图可见,无论是竖向位移、x向应力还是xy向剪应力,均有残余变形,这也验证了我们定义的粘弹性材料的性质。
竖向位移、x向应力以及xy向剪应力的时间历程响应曲线仍有一定的周期波动,波动周期处在0.05 s左右,与该路面结构的第一自振周期相近。而且由图12~图14可见,竖向位移的波动振幅最大,x向应力次之,而xy向剪应力基本为零。这是由于第一振型的振动方向为竖向,说明路面自振对路面结构的响应有影响,特别地,与第一振型方向相同的物理量受到的影响最大。
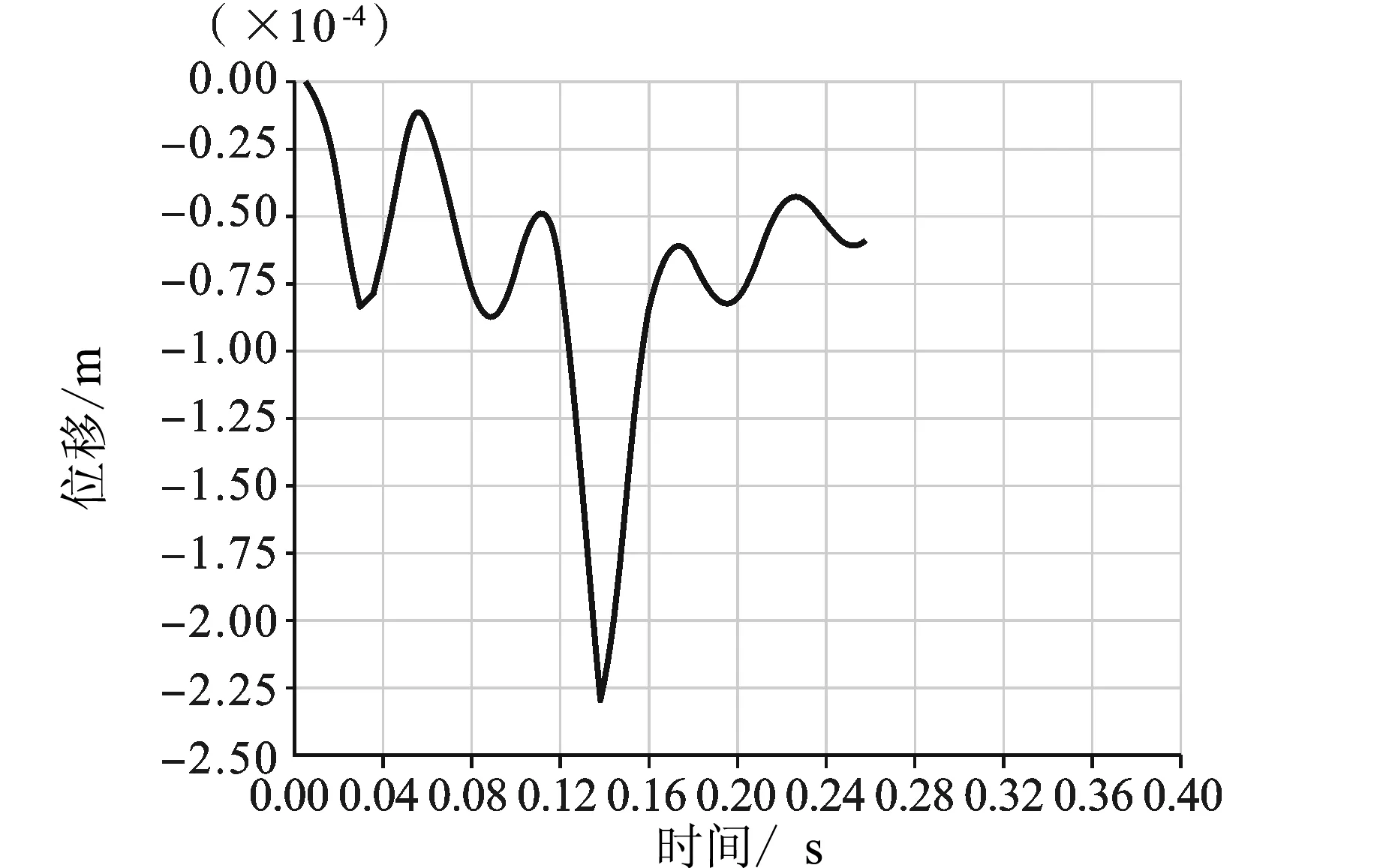
图12 竖向位移的时间历程响应

图13 x向应力的时间历程响应

图14 xy向剪应力的时间历程响应
3 结 论
通过ANSYS有限元软件对实际待铺路面进行了数值仿真,计算出待铺路面在行车荷载下的位移响应、x向应力响应以及xy向应力响应。通过荷载作用下的路面响应特征,得出了位移及应力分布规律,并对其进行了力学解释。发现层间接触状态越好,路面的弯沉响应和应力响应越小;由于沥青材料的“剪切变稀”特性,结合行车荷载下路面的剪切应力分布特征,在轮迹两侧会形成拥包;路面的自振会对同振型方向的结构响应存在较大影响。
[1] Gillespie T D, Karamihas S M, Sayers M W, et all. Effects of Heavy-vehicle Characteristics on Pavement Response and Performance[R]. National Cooperative Highway Research Program Report, No.353, 1993.
[2] Uddin W, Pan Z, Noppakunwijai P, et all. Finite Element Dynamic Analysis of Distressed Asphalt Pavements [C]// Proceeding of 8th ICAP, University of Washington, Seattle, Washington, 1997:725-739.
[3] Zaghloul Sameh, White Thomas. Use of a Three-dimensional Dynamic Finite Element Program for Analysis of Flexible Pavement[R]. Transportation Research Record, n1338, TRB, National Research Council, Washington D C,1993.
[4] 罗 辉. 沥青路面粘弹性响应分析及裂纹扩展研究[D]. 武汉: 华中科技大学, 2008.
[5] JTJ 014-97, 公路沥青路面设计规范[S].
