考虑结构桩土相互作用自升式工作平台研究
2010-01-25吴卫国
李 虎, 吴卫国, 甘 进
(武汉理工大学 a.交通学院; b.高速船舶工程教育部重点实验室, 湖北 武汉 430063)
海上多功能自升式工作平台是为了适应恶劣海洋环境下的桥梁建设而研发的一种新型海洋平台。在恶劣工作环境下,自升式平台结构响应显现出明显的非线性,主要体现在波浪载荷作用及桩土相互作用对平台的影响。现有研究中,对桩土作用的考虑主要是对桩土进行简化处理,本文以某海上自升式工作平台为例,采用ANSYS对该平台进行了三种不同结构与土壤连接形式下的静力和动力特性分析,并对比分析了考虑桩土相互作用和不考虑桩土相互作用下的分析结果,验证了考虑桩土相互作用的必要性。
1 海洋环境载荷的计算方法
海洋自升式平台在复杂多变的海洋自然环境中,将受到风、浪、海流及海冰形成的载荷作用,在地震情况下,它们还将受到地震载荷作用。为了确保平台的安全,设计者必须确定环境条件和外载荷。基于本平台算例所处的地理环境,主要考虑风载荷和波浪载荷。
1.1 风载荷计算
根据《海上移动平台入级与建造规范》[1]第2.2条,风压P按照下式计算:
P=0.613v2
式中,v为设计风速,m/s。
作用于杆件上的风力按下式计算:
F=ChCsSP
式中,P为风压(Pa);S为平台在平浮或倾斜状态时,受风构件的正投影面积(m2);Ch为暴露在风中杆件的高度系数;Cs为暴露在风中杆件的形状系数。
对风载荷,先将受风杆件在不同风向的投影面积、形状系数、高度系数、风压值、风力作用高度等计算出来,然后集中施加在平台上。
1.2 波浪、海流载荷计算
根据《海上移动平台入级与建造规范》[1],计算不同波浪相位角下的波浪载荷和海流载荷,以便确定波流载荷的危险状态。海流力计算时取流向与波浪相位角相同,表面流速为V=0.5 m/s,按照线性规律衰减至海底流速为0。
波浪载荷和海流载荷根据莫里森公式[2]计算:
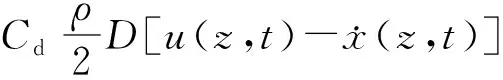
(1)
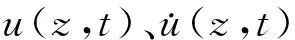
本文选择斯托克斯5阶波浪理论计算波浪载荷,在ANSYS程序中,通过填写PIPE59单元中water table相关参数施加。
2 有限元模型
2.1 平台环境参数及作业参数
本平台为4桩腿(圆壳式)自升式工作平台,钢质非自航。由平台船体、桩腿、升降系统等部分组成[3]。平台工作水深25 m;极限风浪条件:风速45 m/s(蒲氏12级),波高6 m,波周期9 s,潮流速度2 m/s,天文潮高2 m,风暴潮高4 m。平台型长,型宽,型深分别为37.5 m,38 m,4.0 m,桩腿直径2 m,总长53 m,壁厚30 mm。平台总重量2080 t,其中主体钢料965 t,甲板120 t,附属设备995 t。平台最大可变载荷为580 t。
2.2 平台主体的模拟
在总体分析中,由于上部船体结构的强度通常比桩腿结构强度要大的多,故暂不考虑船体部分结构强度[4]。采用Beam4梁单元对船体进行模拟,同时为了减少模型的计算时间,将船体结构简化为互相垂直的四根箱形梁组成的空间框架模型,模型中的梁单元组合截面特性按如下原则进行定义:(1)面积与实际船体截面一致;(2)Y、Z方向的惯性矩与实际船体截面一致;(3)扭转惯性矩与实际船体截面一致。
通过以上的定义,保证模型船体与实际船体刚度一致。泥面以上,水面以下桩腿部分用PIPE59单元模拟;水面以上,船体结构以下及泥面以下桩腿部分用非线性管单元PIPE16单元进行模拟;ANSYS程序对自升式平台进行动力学分析(模态分析和瞬态动力分析)的计算模型与静力分析的计算模型只有一点不同:静力分析时将上部重量(包括设备载荷、结构自重载荷、可变重量载荷等)以载荷形式施加后计算,而动力学分析应将这部分载荷以质量形式来考虑,所以要将其换算成单位长度附加质量填入BEAM4单元的实常数表中。换算方法为:单位长度附加质量=上部重量线载荷值除以9.8[5]。
本文依据不同的约束条件建立了如下三种模型:(1)按照《海上移动平台入级与建造规范》规定,建立泥面下3 m处铰支承模型(图1);(2)插桩情况下考虑桩土相互作用建立的模型,本例中选择插桩深度为20 m(图2);(3)基于API规范,考虑桩靴结构与土壤相互作用建立的模型(图3)。

图1 泥面下3 m铰支承平台模型
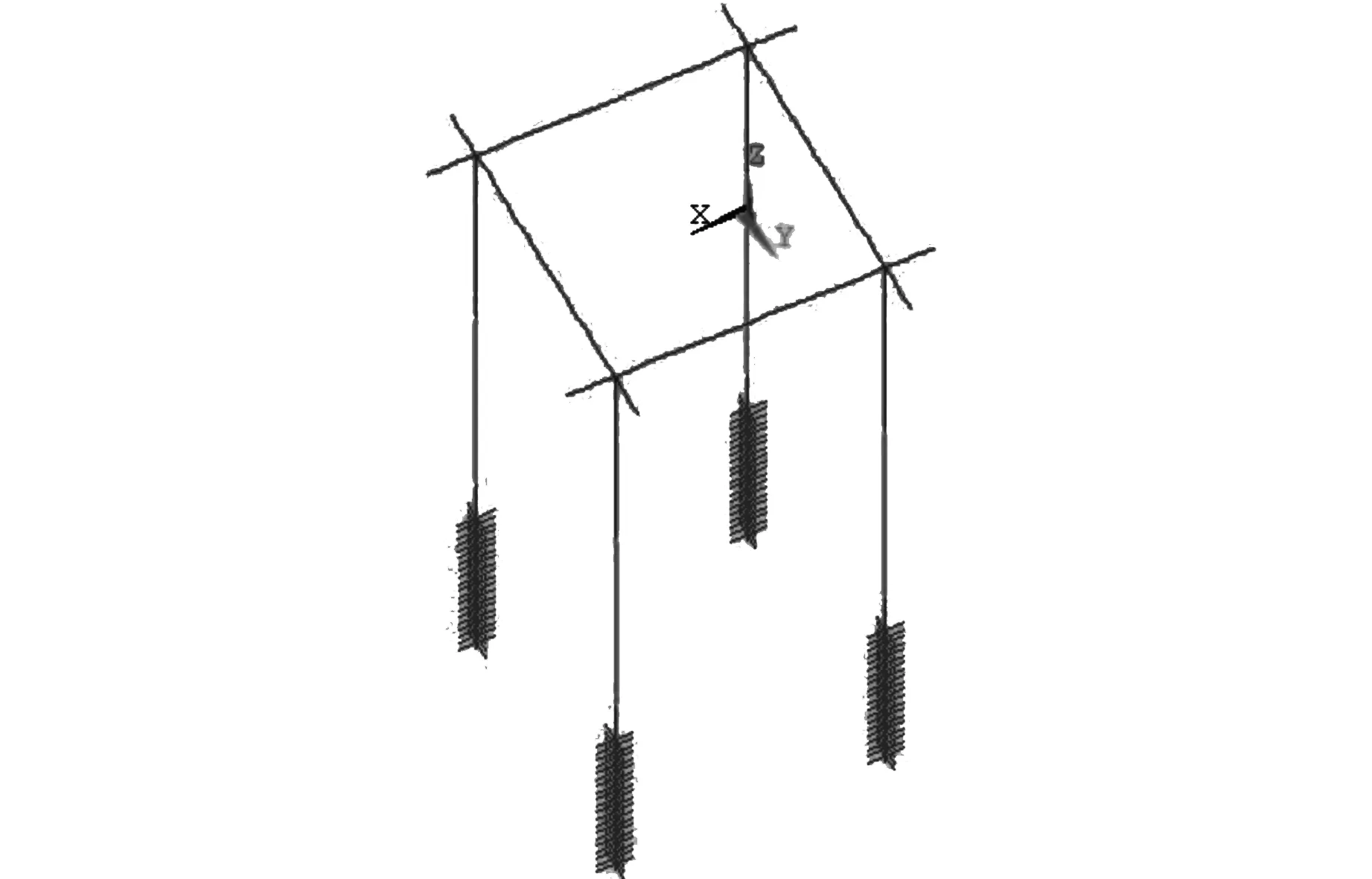
图2 插桩下桩土相互作用计算模型
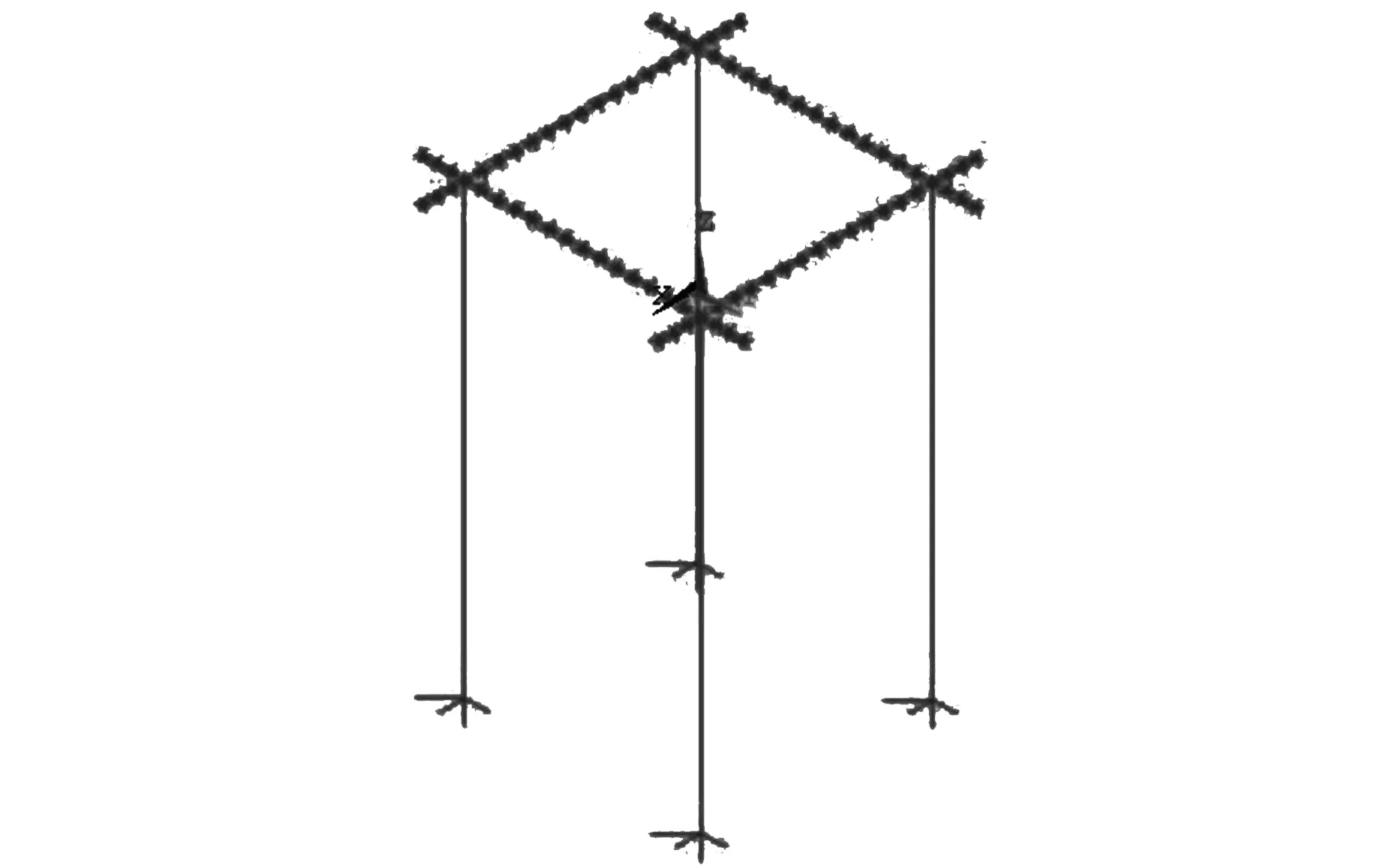
图3 基于API规范的模型
2.3 平台非线性分析
一般对平台进行结构分析时,假定结构发生的唯一远小于结构自升的几何尺度,应变远小于1,故在有限元分析中可以不考虑结构的位置和形状的变化。但对于自升式平台,整体柔度相对较大,而且由于波浪载荷的作用,会使平台产生较大位移,因此进行结构分析时必须考虑动力特性以及变形对平衡的影响[6]。平衡方程和几何关系都是非线性的,于是,变化的几何形状引起了结构非线性的动力响应。所以为了确保安全,仅仅考虑平台的静态效应是不充分的,有必要考虑动力作用,尤其是大位移非线性动力分析。求解非线性问题的有限元方法可分为三类,即增量法、迭代法和混合法。根据自升式平台的结构特点,为减少误差,结构的动力非线性求解采用混合法。混合法的原理在于将荷载划分为较少的载荷增量,而对于每一个载荷增量,进行迭代计算。
在ANSYS程序中,相对于线性分析,非线性分析的不同之处在于:分析选项(Analysis Option)应选择大位移分析选项,并指定适当的子步数;荷载步选项(Load Step Option)应选择时间步选项,并指定为阶跃式加载方式。
3 传统铰接模型研究
3.1 波浪相位角的选取
在算例中,波浪载荷、浮力载荷、海流载荷由ANSYS程序自动施加,其余载荷,如风载荷等,利用ANSYS前处理功能作为集中力或分布力施加。其中在波浪载荷与海流载荷的计算中,ANSYS按海流与波浪所引起的水质点速度的矢量和计算海流与波浪同时作用时的水质点速度。波浪载荷的作用按伪静力方法进行静力分析处理,对波浪相位角φ取不同值对作用于整个结构的波浪力的水平合力的最大值进行搜索,最后以最大合力时对应的φ为输入值进行波浪载荷工况的静力、动力计算[7],在本算例中,φ为35°。
3.2 结构计算结果分析
在波浪入射角为0°、45°、90°时,分别对平台进行静力及动力计算。结构的瞬态动力求解完成后,由ANSYS的时间历程后处理器POST26可以得到结构出现最大位移时节点的水平位移随时间变化的曲线。表1为平台在各入射角下的桩腿顶端最大位移和桩腿约束处最大应力。

表1 泥面下3 m处铰支承模型桩腿最大应力及最大位移
由表1知:由于平台建模时的坐标选取及平台结构自身的对称性特点,最大应力及变形均出现在波、流入射角为0°时。同时,在0°入射下,将计算实例的线性和非线性静力分析的结果进行比较,可以看到桩腿对应的最大应力值的差异在40%以上,对应最大水平位移的差异也达到了60%。两种静力分析结果之间的差异表明,自升式平台柔度相对较大,在结构设计时应进行大位移非线性分析[8]。
在计算实例的瞬态动力分析结果中对应最大应力,最大水平位移的放大系数分别为1.2和1.3以上(见表2),这说明非线性静力分析和动力分析的结果数值相差大于10%。因此对自升式平台进行结构分析时考虑动力计算是有必要的。
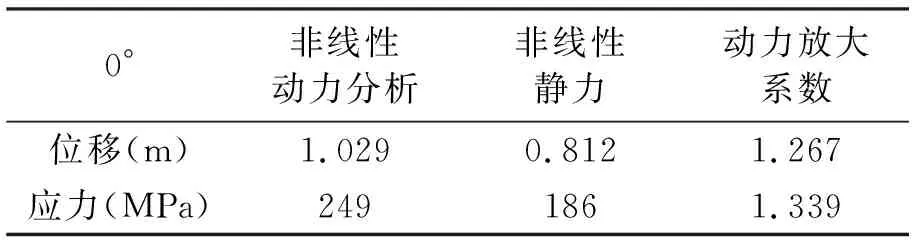
表2 动力分析放大系数
4 桩土相互作用模型研究
桩基础是海洋工程结构物的一种重要结构形式。土与桩的相互作用系统可适当用等效集中的弹簧、阻尼器来模拟[9]。对于现行的钢制自升式平台,平台本身和所处的土介质均存在明显的非线性,泥面以下3m处铰支承处理无法正确反映海洋平台结构体系的整体工作效应,这种分析方法过高的估计了海洋平台结构体系的安全性。本文将海上工作平台结构体系作为一个整体建模分析,在处理平台桩基础与海床作用时,考虑结构与桩土动力相互作用建立以下两种分析模型。
4.1 插桩形式下桩土模型
插桩形式下,采用动力Winkler地基梁模型模拟,土按Winkler地基来处理,桩为埋置于土中的长梁,同时土对桩的影响采用非线性弹簧Combin39单元来模拟,弹簧相应的非线性参数按相应的各土层的轴向载荷传递曲线(t-z曲线)、桩端载荷-位移曲线(q-z)曲线以及侧向载荷-位移曲线(p-y曲线)确定[10]。设计插桩深度为20 m,依据桩周土壤参数,按1 m一段划分单元,避免单根弹簧的作用范围超出某一层土。土对桩的作用简化为三种非线性弹簧,侧向弹簧(土的侧向承载力)、竖向弹簧(桩的表面摩擦力)、端承弹簧(桩的端部承载能力)。相应的弹簧参数根据相应的载荷传递曲线计算得出,填入Combin39单元的F-D参数表。计算模型如图2所示。
4.2 基于API规范模型
模型中充分考虑桩靴与海床的相互作用,边界条件为桩腿最下端采用弹簧六自由度支撑,其刚度系数可用如下公式计算[5]:
k1=2GB/(1-v)
(2)
k2=12GB(1-v)/(7-8v)
(3)
k3=GB3π/180[3(1-v)]
(4)
式中,k1为垂向刚度;k2为水平刚度;k3为扭转刚度;G为土壤剪切模量;B为桩靴长度;v为泊松比。需要注意的是,扭转刚度k3往往需要迭代计算才能最终确定。
4.3 三种模型有限元计算分析
有限元计算软件ANSYS提供了分块兰索斯法[3]等7种模态提取方法。基于海洋平台大型且对称的特点,采用适用于大型对称特征值求解问题的分块兰索斯法对平台模型进行求解,并提取了平台在三种约束条件下的前4阶模态,如表3。
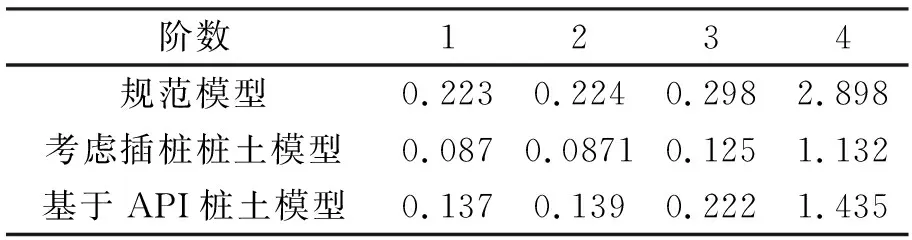
表3 三种模型模态分析结果比较 Hz
由表3知:两种考虑桩土相互作用的模型频率均小于模型1的结果,第一阶对应的自振周期较规范模型大,其原因主要在于两种模型考虑桩腿约束条件的不同。在规范模型中,约束条件为泥面以下3 m处铰支。而桩土模型则考虑了土的存在对桩的影响,用一系列参数不同的弹簧来模拟其对桩腿的约束作用,即在桩腿周围增加了弹性支撑。在插桩形式模型下,与另两种模型相比,桩的长度增加,约束时弹性约束刚度减小,柔度增加,其振动频率明显减小。在基于API规范建立的模型中,考虑了对桩转动方向的约束,但对其所有方向的自由度仍为弹性约束,其振动频率相对铰支承模型要小,介于两种模型之间。

表4 三种模型静力分析结果比较
由表4知:对比静力计算的结果,插桩形式下桩土模型与基于API规范下的桩土模型其桩腿顶端最大位移分别为第一种模型桩腿顶端位移的2.06倍和1.38倍,而相对应的平台最大应力分别大21%和5.4%。由于自升式平台的动力特性,仅仅在泥面下3 m处进行铰支承处理增加了对平台的约束,刚度增大,平台动力响应结果偏小,这对于海洋平台的设计是偏于危险的。通过建立考虑土壤实际参数的平台模型,能够更好的为平台的设计,检测服务,有必要采用更为复杂的桩土模型来替代规范所采用方法来对海上自升式工作平台进行分析。
5 结 语
对自升式工作平台进行非线性动力分析是必要的。桩土作用对平台的动力响应有显著影响,由于土壤对桩基作用的复杂性,有必要依据海上工作平台实际工作环境的土壤参数,建立更合理的桩土模型对自升式平台进行分析。
[1] 中国船级社.海上移动平台入级与建造规范[S].北京:人民交通出版社,2005.
[2] 杨树耕,孟昭英,任贵永.有限元分析软件ANSYS在海洋工程中的应用[J]. 中国海洋平台,2000,15(2):44-47.
[3] 孙东昌,潘 斌.海洋自升式移动平台设计与研究[M].上海:上海交通大学出版社,2007.
[4] 尚小江,邱 峰,赵海峰,等.ANSYS结构有限元高级分析方法与范例应用[M]. 北京:中国水利水电出版社,2006.
[5] 聂 武,刘玉秋.海洋工程结构动力分[M].哈尔滨:哈尔滨工程大学出版社,2002.
[6] 赵晶瑞.自升式平台风暴自存状态桩腿动静强度分析[D].天津:天津大学,2007.
[7] 李远林.波浪理论及波浪载荷[M].广州:华南理工大学出版社,1994.
[8] Hellan Φ,Moan T,Drange S O.Use of Nonlinear Push-over Analysis in Ultimate LimitStateDesign andIntegrityAssessmentof Jacket Structures[C] // 7th International Conference on the Behavior of Offshore Structures,1994:323-345.
[9] GB 50007-2002,建筑地基基础设计规范[S].
[10] 李海波.土壤与地震对自升式钻井平台的作用[D].大连:大连理工大学,2006.
