H型钢腹板轧制波浪的仿真分析

王凤平,孙会朝,马光亭,王培文,王文生

(1.莱芜职业技术学院机电系,山东莱芜,271104;2.莱芜钢铁集团有限公司技术研发中心,山东莱芜,271104)

随着我国H型钢需求量和产量的不断增长,对于H型钢轧制的理论研究也在不断深化。目前,众多研究人员采用有限元方法对H型钢轧制过程进行分析。朱国明等[1-4]采用弹塑性热力耦合有限元方法,完成了大型H型钢全轧程三维热力耦合仿真分析,并进一步对大型H型钢轧后残余应力进行仿真分析,提出了控制大型H型钢残余应力的方法;奚铁等[5-6]借助有限元分析软件SuperFo rm对H型钢开坯轧制及万能轧制过程进行了模拟;徐旭东等[7-8]利用有限元分析方法对H型钢轧制及轧后冷却过程进行二维温度场的模拟,同时采用显式动力学有限元分析方法,模拟了不同变形参数下H型钢的万能轧制过程。

在H型钢轧制过程中,由于腹板和翼缘的压下量分布不均和延伸不平衡,导致腹板内部存在很大的附加应力,当翼缘的延伸率与腹板的延伸率比值(以下简称腿腰延伸比)超过某临界值时,腹板受到的附加压应力超过其屈服极限,腹板产生屈曲失稳,最终形成腹板波浪。

本文采用有限元分析方法,通过调整腿腰延伸比,对H型钢万能轧制过程中出现的腹板波浪现象进行研究,确定在相应孔型中出现腹板波浪的腿腰延伸比临界值,以期为H型钢轧制工艺参数的优化提供参考。

1 轧制工况

选择HN 800 mm×300 mm连轧过程第5连轧道次的第9万能轧制道次(UR)作为研究对象,轧制工艺参数如表1所示,轧制孔型及来料断面形状如图1所示。该道次轧制初始温度场通过全轧程热力耦合的方法得到,轧件断面温度场的分布云图如图2所示。

表1 轧制工艺参数Table 1 Rolling parameters

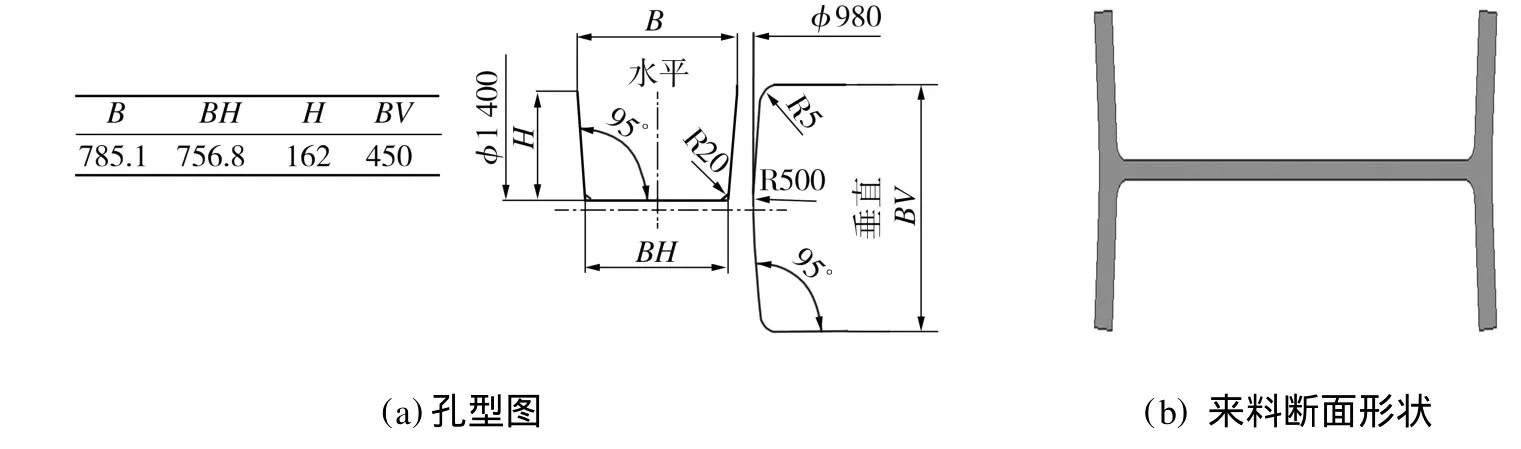
图1 UR轧机孔型图和来料断面形状Fig.1 Sketch of the pass system and stock of UR rollingm ill

图2 轧件断面温度场的分布云图Fig.2 Temperature distribution of stock section

2 仿真模型与仿真工况

2.1 主要边界条件

在H型钢热轧过程中,高温下的轧件通过轧辊的作用产生变形,随着轧制过程的进行,轧件与周围环境的热交换异常复杂,包括轧件与轧辊、传送辊道、轧辊冷却水的热交换以及与周围空气之间的辐射传热和对流传热等。轧件表面与周围空气的对流传热为自然对流下的紊流状态,对流产生的热流密度

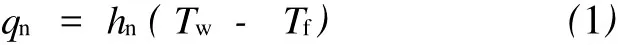
式中:hn为对流换热系数;Tw为轧件表面温度,K;Tf为环境温度,K。针对紊流状态,有:

式中:Nu为努赛尔数;Gr为格拉晓夫数;Pr为空气的普朗特数;α为空气的体积膨胀系数;d为尺寸特性系数,取为0.8;v为空气的运动黏度;λa为空气的热导率。

轧件表面与周围空气的辐射传热系数

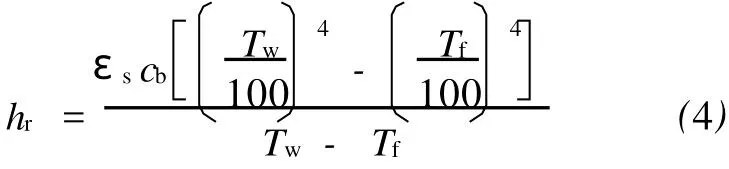
式中:εs为表面发射率,取为0.8;cb为黑体辐射系数,cb=5.669 W/(m2·K4)。

通过热模拟实验得出Q235B钢的导热系数和比热容与温度之间的关系曲线如图3所示。

假设轧制变形过程中塑性功转换为热的有效系数为0.9。轧辊采用刚性辊,轧制过程中轧辊表面温度呈周期性变化,其高温峰值出现在变形区出口,对于热轧板带,该温度可高达500℃,而在变形区入口,轧辊表面温度降至100℃以下。由于本文的研究对象为轧件,在此不考虑轧辊的温度场变化,可假设轧辊温度恒为300℃。轧辊与轧件之间的热交换主要以热传导的方式进行,在变形区内,轧辊与轧件的接触、轧件表面与周围环境的对流和辐射热交换这两个边界条件自动转换为轧件与轧辊之间的热传导,综合考虑以上条件,计算时传热系数设为50 kW/(m2·K)。

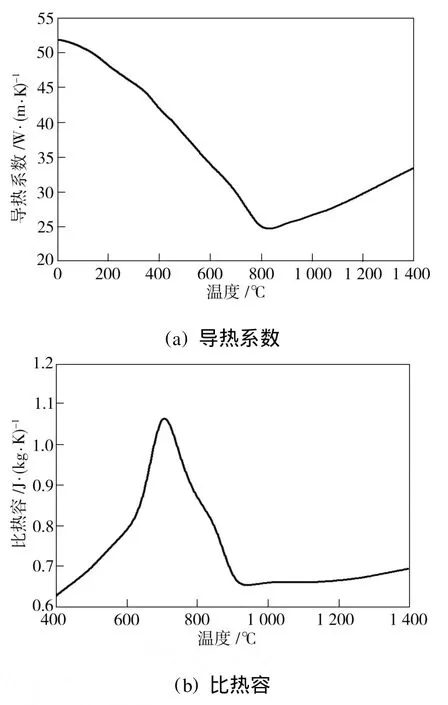
图3 Q235B钢导热系数和比热容与温度之间的关系Fig.3 Relationship between thermal conductivity,specific heat capacity of Q235B steel and temperature

2.2 有限元模型的建立

建立有限元模型时,定义X方向为腹板宽度方向、Y方向为翼缘宽展方向、Z方向为轧制方向。在轧制过程中,轧辊与轧件之间的接触定义为面对面接触方式,轧辊与轧件之间的摩擦采用库仑摩擦模型,摩擦系数设为0.35。UR孔型网格如图4所示。

图4 UR孔型网格图Fig.4 Mesh for the pass type of UR rolling mill

2.3 仿真工况

以第9万能轧制道次的轧制规程为基准,通过改变H型钢轧制时翼缘和腹板的压下量来调整腿腰延伸比λ,制定了16个仿真工况,如表2所示。

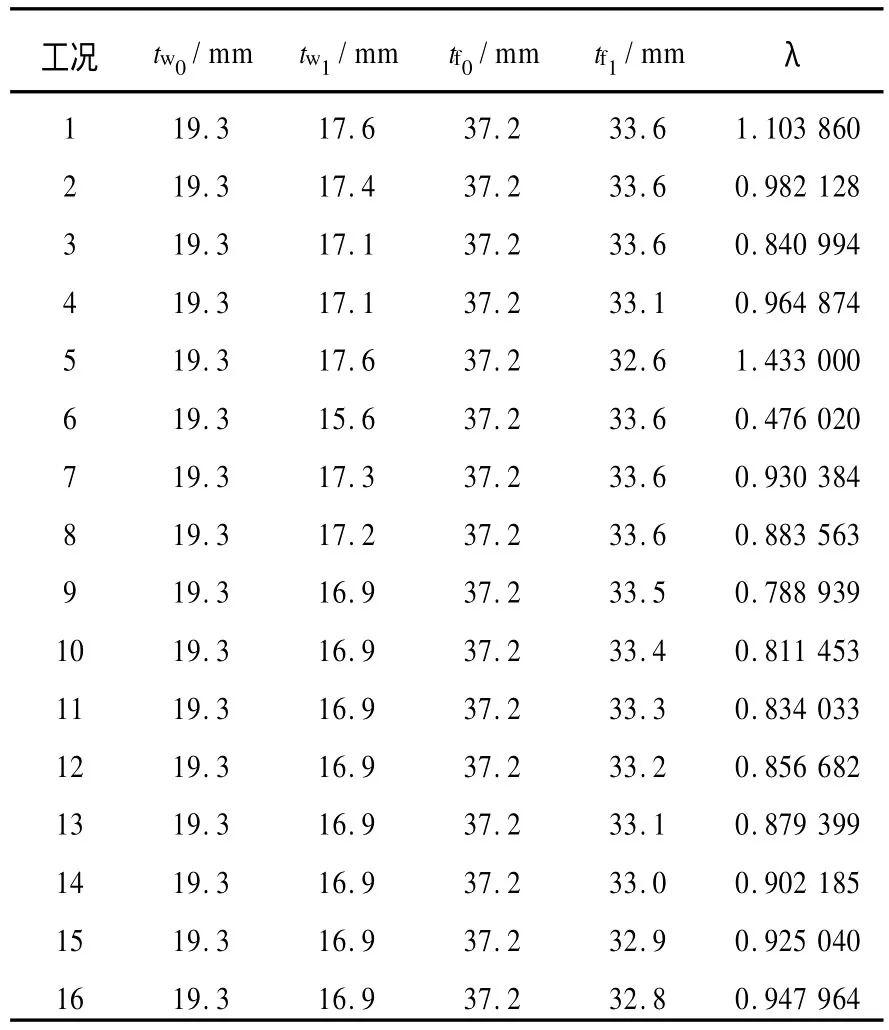
表2 仿真工况基本参数Table 2 Basic parameters of simulation model

3 仿真结果与分析

通过提取腹板上表面节点的计算结果,来比较不同工况下的腹板变形情况。在水平辊压下方向上的轧件将会出现整体位移的现象。在局部范围内,由于存在位移差,在模拟轧制位移云图中将会呈现不同颜色,这样一来,可以通过不同工况的相同时刻下水平辊压下方向的轧件位移云图来判断是否出现腹板波浪。工况12和工况16是两个典型工况,其轧制位移云图如图5所示,从图5中可以很容易看出,工况12出现了腹板轧制波浪,而工况16在轧制过程中没有出现腹板波浪。16个工况的仿真结果如表3所示。从表3中可以看出,当λ<0.93时,H型钢出现腹板波浪。

为了对腹板波浪的产生原因进行更细致的分析,需要提取轧件中间部位关键点及路径的仿真数据,如图6所示。工况12和工况16相同路径上的节点坐标如图7所示。从图7中可以看出,对于工况16,沿轧件长度方向,轧后腹板中心路径上的节点坐标变化不大;而对于工况12,轧后腹板中心路径上出现明显的波浪。提取两个工况下轧件在如图6所示关键点的位移-时间历程曲线,如图8所示。

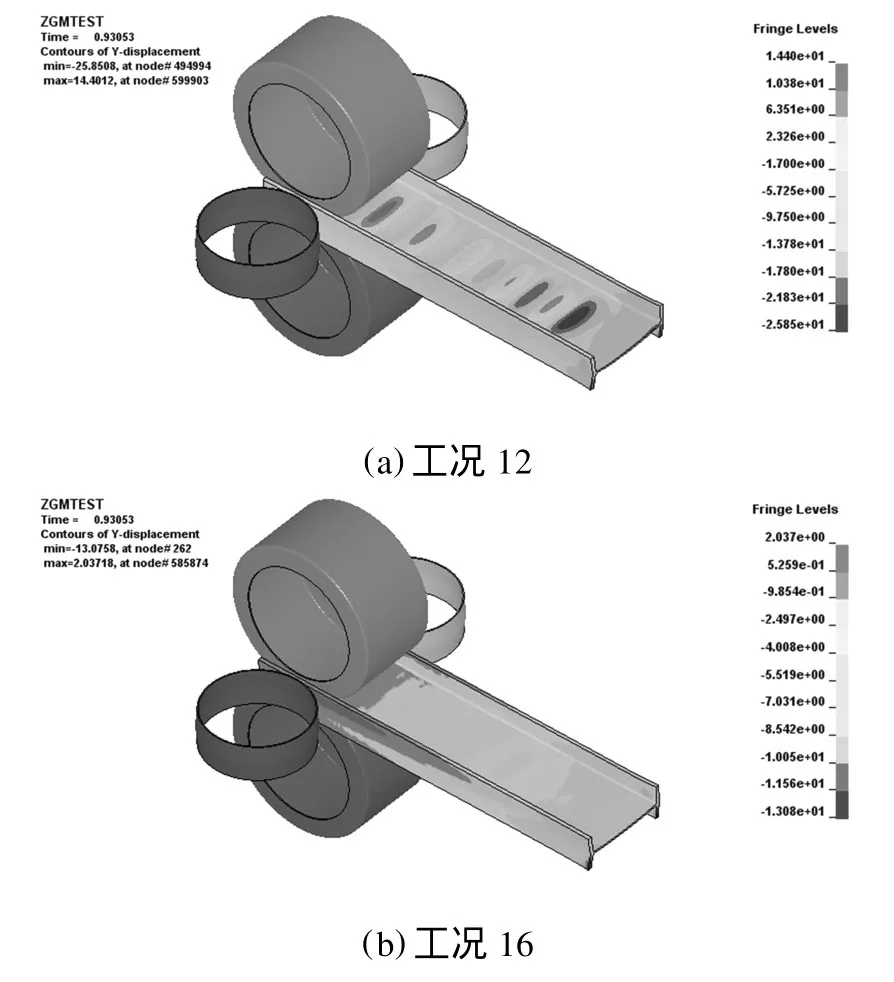
图5 两个典型工况的轧制位移云图Fig.5 Displacement contours of two typical models

表3 不同工况下的仿真结果Table 3 Results of different simulation models

图7 两工况相同路径节点坐标Fig.7 Node coordinates on the same path of two typical models

从图8中可以看出,对于工况12,在轧制过程中,腹板部位关键点的位移在出变形区后发生突变,比在变形区时产生的位移大得多,同时3个关键点出变形区后的位移方向也不同,从而导致腹板轧制波浪的产生。而找出腹板部位关键点位移突变的根本原因,则需要对轧制过程中腹板部位在轧件长度方向上的应力状态进行分析。因此,进一步提取了腹板部位关键点在轧制过程中的应力-时间历程曲线,如图9所示。

图8 两工况关键点的位移-时间历程曲线Fig.8 Display-time curves of the key points on two typical models

图9 两工况关键点的应力-时间历程曲线Fig.9 Stress-time curves of the key points on two typicalmodels

从图9中可以看出,腹板部位关键点沿着轧件长度方向(Z方向)运动,其在变形区内部时承受拉应力,当关键点出变形区后,应力状态突然变化,由拉应力转换为压应力。如果应力状态的变化过大,就会破坏腹板的稳定性,达到一定程度时则出现腹板轧制波浪。与工况16相比,工况12中腹板部位关键点所受压应力要大40～50 M Pa,这正是导致工况12中H型钢出现腹板失稳和腹板波浪的原因。

4 结论

(1)H型钢在轧制过程中产生腹板波浪的主要原因是腿腰延伸比的取值不合理,导致轧件出变形区后,腹板部位的应力状态突然改变,由承受拉应力转变为承受压应力,当压应力增加到一定值时,就会产生腹板轧制波浪。

(2)对于HN 800 mm×300 mm连轧过程第5连轧道次的第9万能轧制道次而言,当腿腰延伸比小于临界值0.93时,H型钢出现腹板轧制波浪。

[1] Zhu Guoming,Kang Yonglin,Chen Wei.3D thermal mechanical coupled elasto-plastic finite element analysis in the w hole rolling process of H-beam[J].Materials Science Forum,2008,575:532-538.

[2] 朱国明,康永林,陈伟.H型钢多道次可逆开坯轧制过程的三维热力耦合仿真分析[J].中国机械工程,2007,18(14):1 747-1 751.

[3] 朱国明,康永林,陈伟,等.H型钢空冷过程中残余热应力的有限元分析[J].机械工程材料,2008,32(4):77-80.

[4] 朱国明,康永林,陈伟,等.降低H型钢残余热应力的三维有限元仿真分析[J].轧钢,2007,24(1):22-26.

[5] 奚铁,钱奕峰,章静.H型钢开坯轧制变形分析[J].轧钢,2004,21(6):47-49.

[6] 曹杰,奚铁,章静,等.H型钢万能轧制变形分析[J].重型机械,2005(1):23-25.

[7] 徐旭东,王秉新,刘相华,等.H型钢控制冷却的有限元模拟[J].钢铁研究学报,2005,17(2):30-33.

[8] 徐旭东,王秉新,刘相华,等.H型钢轧制力的数值模拟分析[J].钢铁,2005,40(7):56-59.