单车型单边装配线平衡调度模型研究

李 明,唐秋华,席忠民,夏绪辉,邓明星

(1.武汉科技大学理学院,湖北武汉,430065;2.武汉科技大学机械自动化学院,湖北武汉,430081; 3.神龙汽车有限公司技术中心,湖北武汉,430051;4.武汉科技大学汽车与交通工程学院,湖北武汉,430081)

单车型单边装配线平衡调度模型研究

李 明1,唐秋华2,席忠民3,夏绪辉2,邓明星4

(1.武汉科技大学理学院,湖北武汉,430065;2.武汉科技大学机械自动化学院,湖北武汉,430081; 3.神龙汽车有限公司技术中心,湖北武汉,430051;4.武汉科技大学汽车与交通工程学院,湖北武汉,430081)

平衡汽车装配线能够提高企业生产效率、稳定产品质量、降低生产延迟。根据单车型单边装配工艺要求,分别以工位间实际操作时间差最小和最大工位持续时间最小为目标,利用0-1变量,建立了混合整数规划装配线调度模型,利用此模型可求得平衡率很高的调度方案。实验证明该模型所得方案是可信的,将其用在装配线设计阶段具有可行性。

混合整数规划;0-1变量;装配线平衡

汽车产品结构复杂,生产批量一般较大,为保证装配质量、提高劳动生产率,生产厂家会根据产品的结构特点,从装配工艺角度将其分解成为可单独组织装配的单元,合理地安排人员、设备和工作地点,组织并行、流水作业。汽车装配涉及上千项操作,而操作间优先关系非常繁杂,如何合理完成操作向各工位的分配,决策各操作的开始时间,使得装配线上各工位负荷尽可能达到平衡,在装配线的设计阶段和生产管理过程中,都是一个不可回避的问题。

装配线平衡可以提高企业生产效率,稳定产品质量,降低生产延迟。该工程问题是典型的NP难问题[1],其数学本质是决策一系列操作向各工位分配的混合整数规划问题。汽车装配操作多,导致离散变量数目繁多,潜在的组合爆炸可能性可能导致实际问题不可求解。

20世纪50年代,Salveson首次提出并建立了单品种装配线平衡问题的数学模型,此后相关的方法被不断提出并应用于求解单边装配线平衡问题。Talbot等[2]采用启发式算法求解装配线平衡问题;Scholl等[3]提出了一种新的启发式算法,得到了简单单车型装配线平衡问题的精确解; Lapierre等[4]利用禁忌搜索算法对装配线平衡问题进行求解;Baybars[5]对简单的装配线平衡问题给出了精确的求解算法;Klein等[6]利用分支定界法求解简单装配线平衡问题。国内对此问题的研究相对较少,张则强等[7]和毛凌翔等[8]分别利用蚁群算法对装配线平衡问题进行了有效的求解。

本文针对汽车装配线平衡问题,考虑各项操作的优先关系和工艺要求,以装配平衡为目标建立单车型单边装配线平衡调度模型,以期为生产线任务分配的设计提供技术支持。

1 单车型单边装配线平衡问题

按所装配车型类型划分,国内汽车装配生产线主要有单车型流水生产线、多车型交替生产线和多车型混流生产线;按工位布局划分,又存在单边和双边之分。由于双边装配的思想与单边装配基本一致,本文以单车型单边装配线为研究对象,建立其装配线平衡的数学模型。

按照单车型单边组织装配生产,一般要求实现以下特征:专业程度高,操作数量多。装配线上的总操作数量很大,但每个工位的工人只从事一个或几个固定操作,以便熟练操作。装配生产具有明显的周期性。完成操作分配后所得操作时间最长工位的作业时间,称为节拍。为保证生产的连续性,要求:①各工位的操作总时间等于或略小于节拍,以防止工位上的任务堆积以及设备或人员的无效等待;②装配线具有异步性和并发性,各工位的状态只在离散时间点上发生跃变,保证生产过程的平衡性和并行性;③工艺路线服从操作逻辑规则,被加工对象在工位间作单向运动。生产线的布置可以是直线式、U型或X型等方式。

在汽车装配生产线上,工人在其工位时间内需要完成多项操作,每项操作的操作时间相对稳定,建模时将其视为常数。同时,为了衡量装配线的平衡程度,引入平衡率 p作为评价指标,定义为

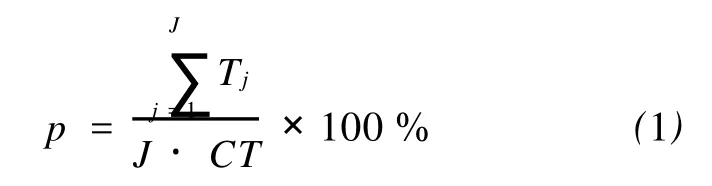
式中:J为工位的总数;Tj表示工位 j(j=1,…, J)的总操作时间;CT为装配线的节拍。

一般地,如果装配线的平衡率为50%～60%时,表明生产线缺乏管理,生产随意;当装配线的平衡率为60%～70%时,表明生产过程管理比较关注平衡问题;当装配线平衡率为70%～85%时,证明生产线的管理十分科学;当装配线的平衡率大于85%时,则认为该生产线的平衡问题得到了很好的解决。

2 单车型单边装配线平衡调度模型

2.1 模型I

在单车型单边装配线上,假设给定操作总数为 I,其序号记为 i,k,i′(i,k,i′=1,2,…,I);假设装配线总共有J个工位,其序号记为 j,j′(j,j′= 1,2,…,J);操作 i的实际操作时间记为ti。为了表征操作间的优先关系,引入直接优先集 P= {(i,k)},对于任意(i,k)∈P,表示操作 i直接优先于操作k。

定义实数变量 Startij,表示在工位 j上操作i的开始时刻,如果任务i不在工位j上,则相应变量为0。为了确定操作i是否在工位j上,引入0-1决策变量 xij,定义 xij=1表示操作 i在工位 j上,否则 xij=0;为了确定两个操作 i和k的先后关系,引入0-1决策变量Orderik,定义Orderik=1表示操作i优先于操作k,否则Orderik=0。在决策前,根据装配线的逻辑顺序和几何要求,部分操作间的优先关系(包括直接优先关系和间接优先关系)已经确定,所以对这部分操作相应的决策变量可以直接赋值,以提高计算效率。

决策变量 xij和实数变量 Startij之间存在内在的联系,即如果 xij=1,则在工位 j上操作i的开始时刻Startij应满足 Startij≥0,否则 xij=0,此关系可用下式描述:

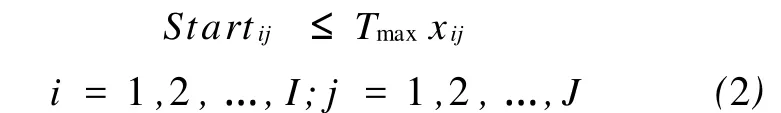
式中:Tmax为常量,表示一个较大的时间,可取作所有操作的操作时间之和。

在装配生产线上,操作i必须被执行并且只能在一个工位上进行,即应满足

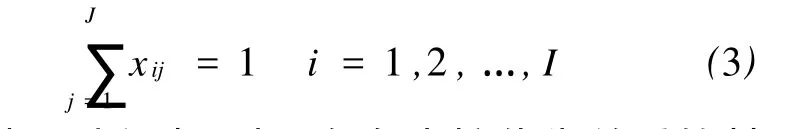
在装配过程中,对于存在直接优先关系的某两项操作i和k,显然不论它们是否在同一个工位中,都应满足

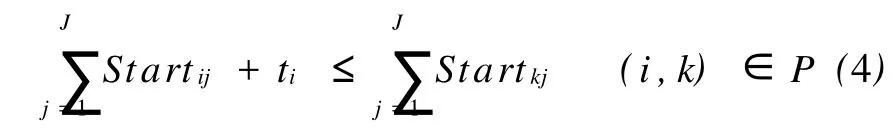
汽车装配线是流水作业,即对同一个工位上的两项不同操作i和k,其关系必须是串行的,此串行关系可利用下面两个不等式进行控制

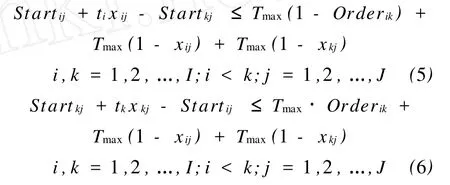
对相邻的两个工位,一般要求前一个工位结束后才能进行下一个工位,但如果空间上允许,这两个工位之间允许有一定的重叠时间,为此引入常量 Toverlap表示相邻两个工位重叠时间的上界,则前一个工位的结束时间与后一个工位的开始时间之间应满足下面不等式:

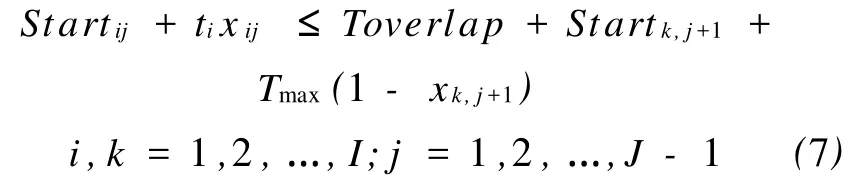
考虑到操作的不可分割性,在各个工位,工人装配汽车零件时允许有闲置时间,但此闲置时间应尽可能小,为此引入常量 Tid le表示各工位闲置时间的上界,显然各工位的实际操作时间和持续时间应满足下面不等式:

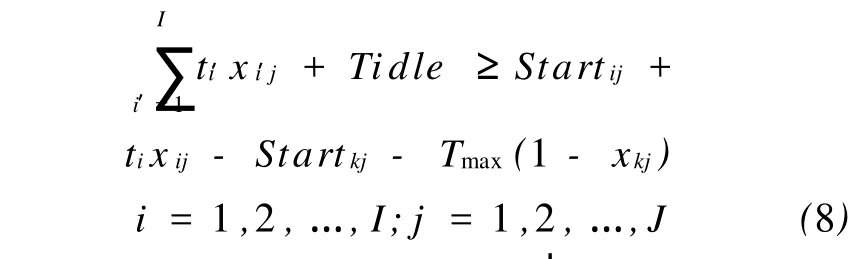
考虑到目标函数为非线性函数,引入下面不等式将其线性化:

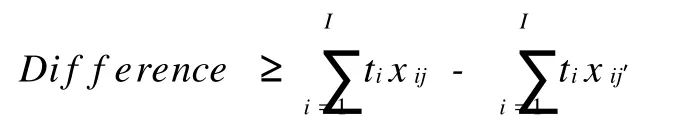
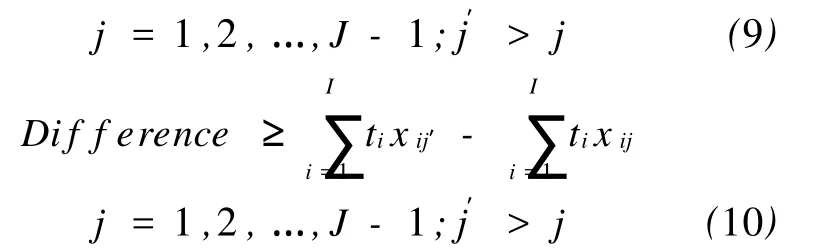
式(2)～式(10)即为单车型单边装配线平衡问题的调度模型,记为模型Ⅰ。

2.2 模型Ⅱ

在模型Ⅰ中,约束条件(8)的目的在于使得各工位的闲置时间尽可能地小,即不超过 Tid le,目标函数式(9)、式(10)的目的在于使得各工位的平衡度尽可能地高,这两个目的也可以由下式一并完成

式(2)～式(7)与式(11)称为单车型单边装配线平衡问题的调度模型Ⅱ。

2.3 模型Ⅰ与模型Ⅱ的寻优思想比较

模型Ⅰ和Ⅱ都以提高装配线平衡为目标,但其寻优思想略有不同。如图1(a)所示,模型Ⅰ通过最小化最长和最短实际工位操作时间差异,使得各工位的实际操作时间尽可能相等;而模型Ⅱ则通过最小化最大工位持续操作时间,使得各工位的操作时间达到平衡,如图1(b)所示。此外模型Ⅰ考虑的是实际操作时间长度,可以保证工位内部无闲置时间,而模型Ⅱ则最小化工位持续时间,其中包含闲置时间。

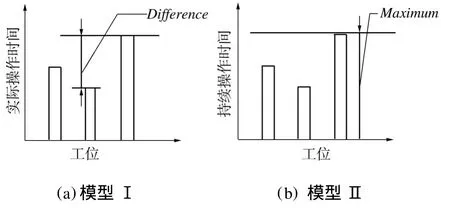
图1 模型Ⅰ和模型Ⅱ的寻优思想差异示意图Fig.1 Optim ization difference between modelⅠand modelⅡ

3 算例

假设某汽车装配线需要在3个工位上完成16项操作,各项操作的实际操作时间和操作之间的优先关系如见图2所示。

将图2中的数据分别代入模型Ⅰ和模型Ⅱ,利用GAM S软件求解,结果如表1所示。绘制装配线平衡调度方案甘特图如图3和图4所示。

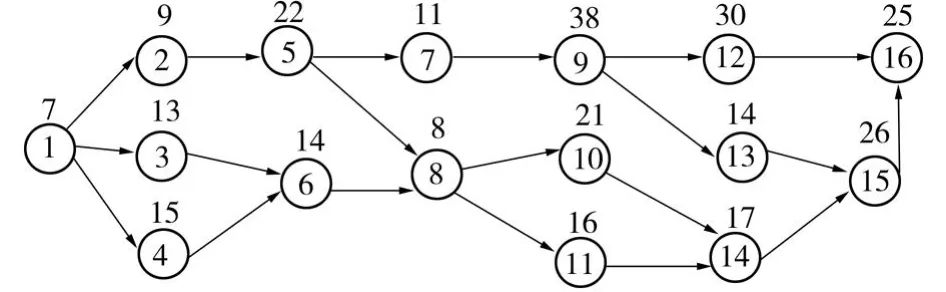
图2 单车型单边装配线操作优先关系图Fig.2 Dom inance relationship of the one-side assembly line

由表1中可见,两个模型求解所得装配线调度方案的平衡率都很高,表明模型所得单车型单边装配线调度可以达到很好的平衡。此外,模型Ⅰ能够控制工位内部的闲置时间(本例中为0),而模型Ⅱ则只能使得此闲置时间尽可能小(本例工位2中闲置时间为1),算例所得结论与前面模型的理论分析相一致,表明模型及其求解方法是有效的。

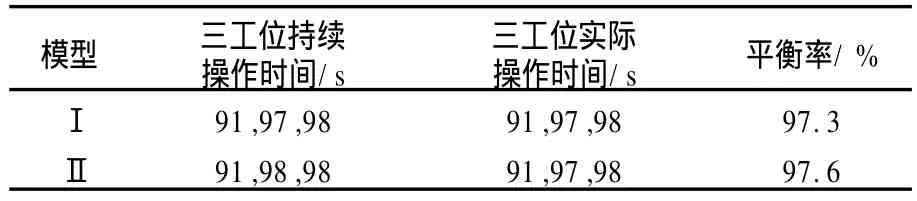
表1 模型Ⅰ和模型Ⅱ的求解结果Table 1 Solutions of modelⅠand modelⅡ

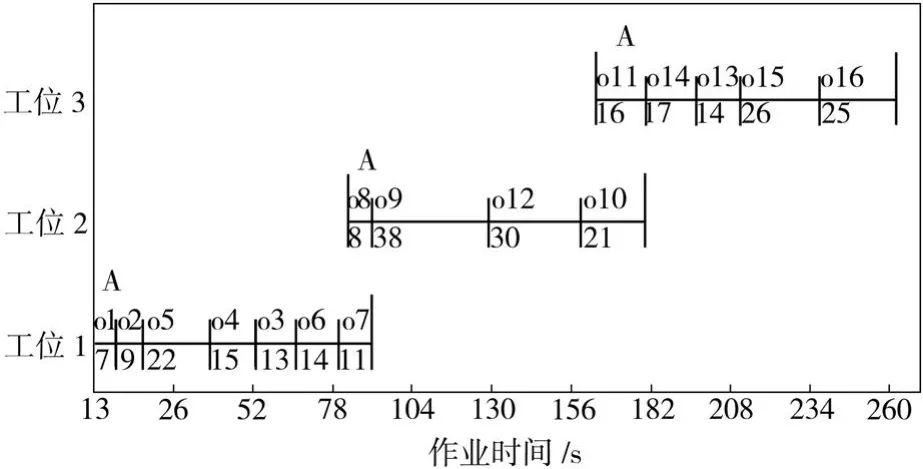
图3 模型Ⅰ所得装配线调度方案甘特图Fig.3 Gantt chart of the assembly line from model I

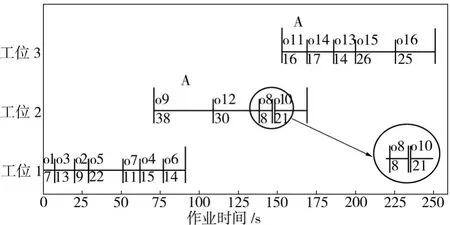
图4 模型Ⅱ所得装配线调度方案甘特图Fig.4 Gantt chart of the assembly line from modelⅡ

[1] Bartholdi J J.Balancing two-sided assembly lines:A case study[J].International Journal of Production Research,1993,31:2 447-2 461.

[2] Talbot F B,Patterson J H,Gehrlein W V.A comparative evaluation of heuristic line balancing tech-niques[J].Management Science,1986,32:430-454.

[3] Scholl A,Becker C.State-of-the-art exact and heuristic solution p rocedures for simp le assembly line balancing[J].European Journal of Operational Research,2006,168(3):666-693.

[4] Lapierre SD,Ruiz A,So riano P.Balancing assembly lines w ith tabu search[J].European Journal of Operational Research,2006,168(3):826-837.

[5] Baybars I.A survey of exact algo rithm s fo r the simp le assembly line balancing p roblem[J].Management Science,1986,32:240-253.

[6] Klein R,Scholl A.Maximizing the p roduction rate in simple assembly line balancing—a branch and bound p rocedure[J].European Journal of Operational Research,1996,91(2):367-385.

[7] 张则强,程文明,钟斌,等.求解装配线平衡问题的一种改进蚁群算法[J].计算机集成制造系统,2007, 13(8):1 632-1 637.

[8] 毛凌翔,郑永前.蚁群算法求解装配线平衡第一类问题[J].计算机系统应用,2009,19(1):140-143.

Balancing of single-model one-sided assembly line models

L i M ing1,Tang Qiuhua2,X i Zhongm in3,Xia Xuhui2,Deng M ingxing4
(1.College of Science,Wuhan University of Science and Technology,Wuhan 430065,China; 2.College of Machinery and Automation,Wuhan University of Science and Technology,Wuhan 430081,China; 3.Technical Center,Dongfeng Peugot Citroen Automobile Company L td.,Wuhan 430051,China; 4.College of Automobile and Traffic Engineering,W uhan University of Science and Technology,Wuhan 430081,China)

Balanced automobile assem bly line can raise p roduction efficiency,stabilize p roduct quality, and reduce p roduction delay.M ixed integer p rogramming assembly line scheduling model is established w ith binary variable according to the assembling specificationsof single-model one-sided line to minimize the difference between each station time and the duration time of the maximum station respectively,and two high balance rate scheduling p rogram s are obtained acco rding to the model.The experimental results show that the scheme is p romising and feasible w hen emp loyed in assembly line design.

mixed integer p rogramming;binary variable;assembly line balancing

TH181

A

1674-3644(2010)06-0620-04

[责任编辑 郑淑芳]

2010-06-17

国家自然科学基金资助项目(50875190/E051005).

李 明(1976-),男,武汉科技大学讲师.E-mail:lmzqx@163.com