隧道工程测量的精度分析与测量方案设计

李致宇,孙海燕

(武汉大学 测绘学院，湖北 武汉 430079)

由于隧道施工的特殊性，测量工作对于保证隧道施工质量以及进度都起到十分重要的作用.隧道工程由地上部分及地下部分组成，而且大型隧道工程往往分为不同的标段，由多个施工单位在若干个工作面施工完成.一个完整的、合理的测量技术方案，是协调施工的各阶段、各单位的基本保证.

隧道施工及隧道施工测量的关键技术指标是横向贯通误差.地面控制测量、地下导线测量及联系测量的误差是导致隧道贯通误差的三个主要因素.为保证贯通误差小于设计值，需从贯通误差的限差出发，对各阶段的精度指标进行整体设计，给出各阶段的测量精度要求，从而既能让各阶段的测量工作顺利进行，又能保证最终的工程质量.如果没有测量精度的整体分析，则可能由于测量精度要求偏低造成质量事故，或是由于测量精度要求过高，使得测量工作量大大增加，造成人力物力的浪费和工期的延误.本文对影响隧道贯通的不同测量阶段的精度及其对贯通误差的影响进行了详细分析，提出了基于贯通误差限差“按需分配”原则进行测量方案设计的方法.通过必要的数值计算，为多种隧道工程的测量方案设计提供比较直观的理论参考.

1 贯通误差的主要来源

贯通误差主要受地面控制测量、联系测量和地下导线测量的误差的影响.上述测量阶段是三个独立过程，所以可将其对于贯通误差的影响作为相互独立的因素予以分别研究[1].对于横向贯通中误差Mq贯可表示为：

(1)

式中mq控上为地面控制测量误差影响值，mq联为联系测量误差影响值，mq控下为地下导线测量误差影响值.

我国《新建铁路工程测量规范》中对于不同长度对向开挖隧道的横向贯通误差的限差做了明确规定，比如长度为4～8 km的隧道，横向贯通误差的限差为150 mm[2].限差通常为中误差的两倍，所以在进行技术方案设计与误差分配时应取横向贯通中误差Mq贯为限差的一半.

表1 “等影响”原则横向贯通误差分配表(mm)

测量误差对隧道贯通的影响与施工方法密切相关.从工程测量的角度看，可以将一个对向开挖段作为一个独立单元进行分析.若对向开挖段长度相差较大，测量方案设计需要对其贯通误差分别进行分析.若各段长度大致相同，则可取其中最长的一段进行分析，作为对各段贯通误差分析的代表.不论是那种情况，每个对向开挖段均为独立的分析单元，分析方法都是一致的.

对于一个对向开挖段的贯通最为不利的施工方法是通过两个竖井对向开挖.这种情况下，影响隧道贯通的测量误差因素有地面控制、两个竖井的联系测量、地下的两条支导线测量，共有三类、五个独立的误差因素.如果有一端是通过平洞或者斜井进行开挖，则应去掉相应的联系测量的误差.

常规的隧道施工测量误差分配原则是“等影响”原则[1]，即认为各个独立因素误差相同，于是每个独立因素对于横向贯通误差的影响值mq可表示为：

(2)

式中Mq贯为隧道横向中误差允许值，N为独立误差因素的个数.

根据式(2)可以计算出得到“等影响”原则下不同长度隧道(km)对于不同个数的误差因素分配到的允许误差(mm)，见表1.

由于现代测量技术及仪器设备的进步，使得有些测量工作能够以较小的代价达到很高的精度.比如地面控制测量，采用GPS技术达到毫米级精度是比较容易的，地下导线测量的精度也随全站仪测角、测距精度的提高有了较大的提高，而联系测量的方法尽管有所改进，但带来的好处主要体现在降低劳动强度和提高工作效率上，其精度与传统方法几乎没有差别.如果现在仍然采用“等影响”原则，一方面无法发挥先进技术的优势，另一方面也不能照顾到技术的薄弱环节.所以在隧道施工测量中，“等影响”原则已经不适应当前的测量技术.我们需要按照隧道工程测量不同阶段的技术特点，或者说需要按照不同的误差因素的特点进行贯通测量误差的分配.这里不妨称之为“按需分配”原则.

为了达到这一目的，就需要对各阶段的测量误差对横向贯通误差的影响进行分析，从而得到合理、高效的测量技术方案.下面对各误差因素对于横向贯通误差的影响分别进行分析并逐步阐述根据“按需分配”原则进行允许误差分配的方法.

2 地面控制测量对于横向贯通误差的影响

地面首级控制测量是隧道施工测量的第一步，后续各阶段的测量工作均以此为基础逐步展开.影响隧道横向贯通误差的地面控制测量误差可以分为两部分：

(1)洞口(近井)点坐标的误差：洞口(近井)点坐标的误差将通过联系测量与地下导线传递到贯通面，严格地讲，它对贯通误差的影响在数值上等于同一隧道开挖段两洞口(近井)点的相对误差椭圆在贯通面上的投影.影响隧道贯通误差的是控制网的相对误差，而不是其绝对误差.可以对问题作进一步的简化，若把隧道一端的洞口点视为固定点，则另一洞口点相对于该点的误差不会超过整个控制网最弱点的点位误差.因此，可以把最弱点的点位误差近似地看作为控制网的点位坐标误差对于贯通误差的影响.

(2)地面控制网边的方向误差：这种误差表现为联系测量或地下支导线的起始方位的误差.不论联系测量采用何种形式，地面控制网边起始方位误差对贯通误差的影响都是一样的.设地下单侧支导线的总长度在贯通面的垂直方向上的投影为S0，则地面控制网边的方向误差对横向贯通误差的影响值为起始方向误差与S0的乘积.控制网中某边的方向误差，可以看作为其垂直方向上控制网的边长误差.若以相对误差计，则其数值不大于控制网最弱边的相对误差，故可对控制网最弱边的相对误差作精度要求.

地面控制测量误差对横向贯通误差的影响就是上述两部分误差的合成.近似认为隧道在中间贯通，则有下式：

(3)

如果采用优化设计的方法进行地面控制网的设计，可以将隧道各开挖段两端的控制点相对误差及定向边的方向误差作为设计的精度指标.若用常规方法设计控制网，则可用前述讨论中的最弱点的点位误差和最弱边的边长相对误差作为精度指标.后两个精度指标与通常评价控制网精度的指标完全一致，在应用上更加方便.

在上述讨论中，假定洞口(近井)点为地面控制网点.如果洞口(近井)点通过加密得到，则须考虑加密误差，或者采用联合平差的方法，将首级网点与加密点进行整体分析.

图1 一井定向示意图

3 联系测量对于横向贯通误差的影响

根据隧道工程的特点，起始方位角误差对于贯通误差的影响随地下导线长度的增加而显著增加[1].如果通过平洞或斜井进行开挖，地下导线的起始方位就是地面控制网的方位角，其误差对贯通误差的影响在上一小节已有论述.若是通过竖井施工，地下导线起始点位坐标与方位角需要通过竖井联系测量得到.下文将以一井定向为例分析联系测量误差对于隧道横向贯通误差的影响.

通过一个竖井进行联系测量(见图1)，需在井筒内设置两条垂线O1与O2(悬挂两根钢丝或使用激光铅垂仪)，在地面测量角度ω及联系三角形AO1O2的图形元素(边a,b,c、角α)，在地下测量角度ω1及联系三角形O1O2A1的图形元素(边a,b1,c1、角α1)，然后计算得到A1点的坐标与方位角αA1M，此即为地下导线的起始点与起始方向.

根据上述图形所给定的几何条件和简单的平差，容易确定点A1坐标及其中误差.A1点坐标误差对隧道贯通的影响与地面控制点坐标误差的影响相同，其数值与地下导线起始方向误差的影响相比可以忽略不计，所以在联系测量的误差分析中，本文只考虑起始方位角误差对隧道贯通的影响.

地下起始方位角αA1M的误差可用下式表示：

(4)

式中(mo方)s为测边误差所引起的角度计算误差；(mo方)β为测角误差的影响.

根据图1所示几何关系，考虑地上联系三角形AO1O2与地下联系三角形A1O1O2相似且α及β为小角.利用误差传播定律[4]，可分别得到由测边、测角误差所引起的地下起始方位角误差的计算公式[1]：

(5)

式中(mo方)s为测边误差所引起的角度计算误差；ms为测边误差；其余各因子为联系三角形元素.

(6)

式中(mo方)β为测角误差的影响；m上与m上下分别为地上和地下测角误差；其余各因子为联系三角形元素.

将式(5)与式(6)代入式(4)，即可得到地下起始方位角误差.其对单侧横向贯通误差的影响就是方位角误差与单侧支导线在贯通面垂直方向上的投影长度的乘积.选取对精度有利的联系三角形元素：α=3o和a/b=1.5[1]，对于不同的角度和边长测量精度、竖井直径d(m)及隧道长度2L(m)，可算得起始方位角误差对横向贯通误差影响值(cm)，具体数值见表2.

通过表2可以看出：以一井定向为代表的联系测量，传入地下的起始方位角误差对于横向贯通误差的影响将随着隧道长度的增加而显著增长.当隧道小于4 km时，按照“等影响”原则分配允许误差并实现联系测量并不困难，但当隧道长度达到10 km时，即使采用表2中精度最高的测角、测边组合进行联系测量亦无法满足要求.比较现实的办法就是给联系测量分配更大的允许误差.

表2 地下起始方位角误差引起的单侧横向贯通误差(cm)

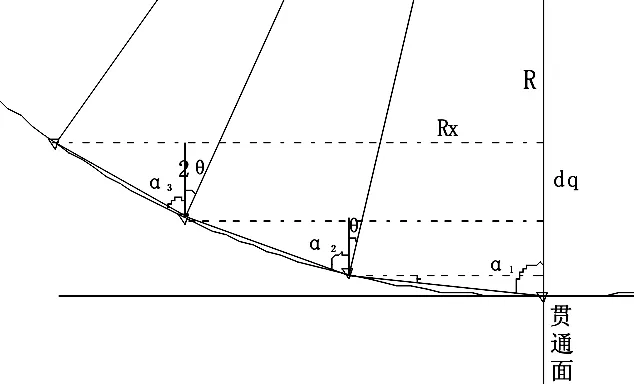
图2 曲线隧道地下导线示意图

4 地下导线测量误差对于横向贯通误差的影响

地下导线测量误差对横向贯通误差的影响可表示为：

(7)

其中mq地下为地下导线测量对于横向贯通误差的总影响；mqβ为地下导线转角测量误差引起的横向贯通误差；mql为地下导线边长测量误差所引起的横向贯通误差.

隧道贯通前，地下导线为支导线，所以式(7)可以写成[1]：

(8)

(9)

式中mq为单侧导线测量引起的横向贯通误差影响值；mβ为等精度测角中误差.

利用式(9)，选择不同的导线长度l(m)，测角误差和几种不同的隧道长度2L(m)，可得直线型隧道地下等边直伸导线测量引起的横向贯通误差(cm).计算结果见表3.

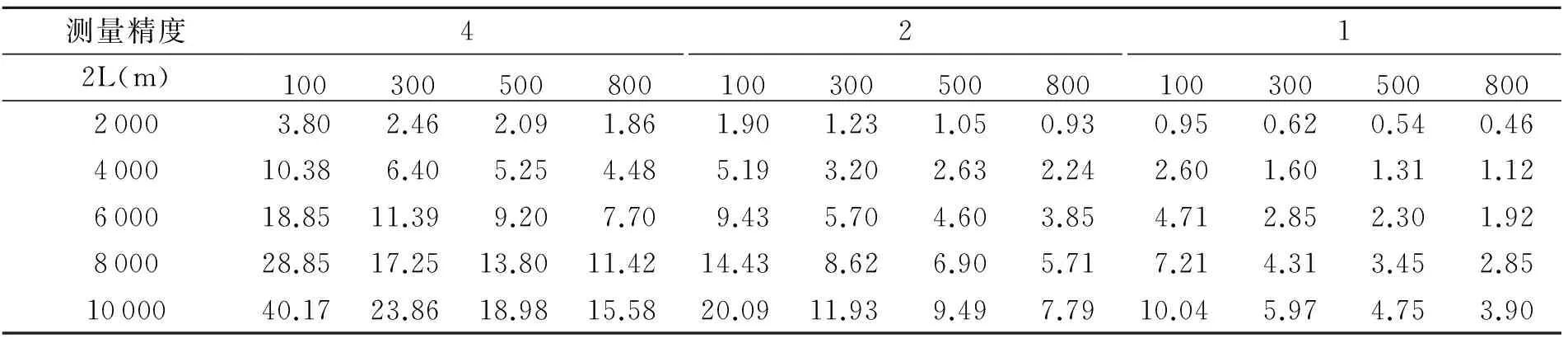
表3 等边直伸导线误差引起的单侧横向贯通误差(cm)

若隧道为曲线，则测角误差与测距误差都会影响贯通.以图2所示的圆曲线型隧道为例，设隧道的转角α=30°，隧道中线全长2L，隧道洞宽20 m，圆曲线半径为R=(2L/α).根据圆曲线的半径及隧道宽度，导线的边长l通常在100m至800m之间.仍假设在隧道中央贯通，即贯通长度为L.单侧支导线的边数为N(近似以导线长度代替隧道中线的长度)，导线点均位于隧道中线上.

由图2及式(7)、(8)知，由测角误差和测边误差所引起的单侧横向贯通误差分别为：

(10)

(11)

式中mβ为等精度测角中误差；R为圆曲线半径；θ如图2所示为圆心角；ml为导线测边误差；l为导线长度.则不同的测角和测边精度、导线长度l(m)对于不同长度2L(m)隧道横向贯通误差的影响(cm)，可利用式(10)和(11)分别进行计算，相应得到表4和表5.表中的数字-1表示不宜布置与之对应长度的导线边.

表4 曲线型隧道测角误差引起的单侧横向贯通误差(cm)

表5 曲线型隧道测边误差引起的单侧横向贯通误差(cm)

式(10)、(11)及表4、5的计算表明，对于曲线型隧道，导线测量的角度误差和边长误差均影响贯通.当隧道转角比较大时，控制边长测量的误差，对于保证隧道贯通亦有较大的作用.这是与直线型隧道不同的地方.

不论是直线型隧道还是曲线型隧道，导线各边长测量误差对于贯通的影响是独立的，影响值与该边在贯通面上的投影成正比，但与该边在导线中的位置无关.导线转角测量误差对于贯通的影响则与其所处的位置有关，离隧道贯通面越远，转角测量的误差对贯通误差的影响越大，其数值与该角顶点到贯通面的垂直距离成正比.尽量加长导线边并适当提高靠近洞口的导线转角测量精度，可大幅度减小贯通误差.当精度要求较高时，可以采用不等权的方式设计地下导线的观测方案，适当提高靠近起点的转角的测量精度.

5 算例

设一长度为8 km的直线型隧道，横向贯通误差的限差为20 cm.一侧采用竖井、一侧采用斜井进行对向开挖，贯通面位于隧道的中间.根据上述讨论，按照允许横向贯通中误差为10 cm可作如下精度设计.

表6 测量精度设计与误差分配表

本例中的隧道一侧采用竖井，另一侧采用平洞(或斜井)进行对向开挖，独立误差因素为4个.按照“等影响”原则，从表1可知每个独立误差因素可分配3.7 cm的允许影响值.此时根据表2与表3的估算，联系测量与地下导线测量均须采用最高精度施测才能满足要求.表6跟据“按需分配”原则给出了三套测量精度设计与允许误差分配方案，在满足允许贯通误差的前提下，误差分配照顾到了施工测量的薄弱环节，避免了允许误差分配不足或分配浪费现象的发生.

6 结语

本文详细分析论述了影响隧道贯通的各个测量环节的误差因素的数值及特点.据此可以从整体上进行测量方案的设计，使得既能保证隧道安全贯通，又能使各环节的测量工作顺利完成.在误差分析的基础上，根据“按需分配”原则进行允许贯通误差的分配，不再拘泥于“等影响”分配原则，可以比较灵活地制定施工测量方案，从而以较小的工作量完成隧道施工测量任务.这对于保证质量、节省工期和测量费用都有重要的意义.

[1]李青岳,陈永奇.工程测量学(第2版)[M].北京:测绘出版社,1995:194-245.

[2]铁道部.新建铁路工程测量规范TB0101-99[M].北京:中国铁道出版社,1999:29-31.

[3]姚连璧,沈云中,胡丛玮，等.铁路隧道GPS网布设的精度分析[J].武汉测绘科技大学学报,1997(2):180-183.

[4]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003:23-58.

[5]张项铎,张正禄.隧道工程测量[M].北京:测绘出版社,1998:38-76.