两种常见坐标系向Authorware窗口坐标系的转化
2010-01-18于万国
于万国
(河北大学,河北保定071002)
在课堂教学中,经常在直角坐标系或极坐标系下绘制函数曲线或图像,但在Authorware中,如果将函数公式直接运用到图形的绘制上,会发现在演示窗口上绘制的图形并未按照直角坐标系中的规律绘制.原因就是Authorwre窗口坐标系与直角坐标系有明显的区别,本文从Authorwre窗口坐标系的特点入手,研究了直角坐标系、极坐标系向Authorwre窗口坐标系的转换,关键是直角坐标系向窗口坐标系的转换,因为极坐标可以先换算成直角坐标,再由直角坐标向窗口坐标转换.供经常用Authorware制作图形的读者参考.
1 Authorware窗口坐标系的特点
首先,窗口坐标系是一种绝对坐标系,坐标轴的原点在演示窗口的左上角,计算机可以识别、位置不可更改,窗口坐标系的坐标负值都不在可视范围内[1].而直角坐标系是一种相对坐标系,其原点的位置可以根据需要确定在窗口的任意位置上,其位置可以移动.
其次,窗口坐标系坐标轴的正方向分别为:横坐标水平向右递增,纵坐标垂直向下递增.而直角坐标系的纵坐标按照一般习惯总是垂直向上递增的 (当然也可以人为地设定向下).如图1所示.
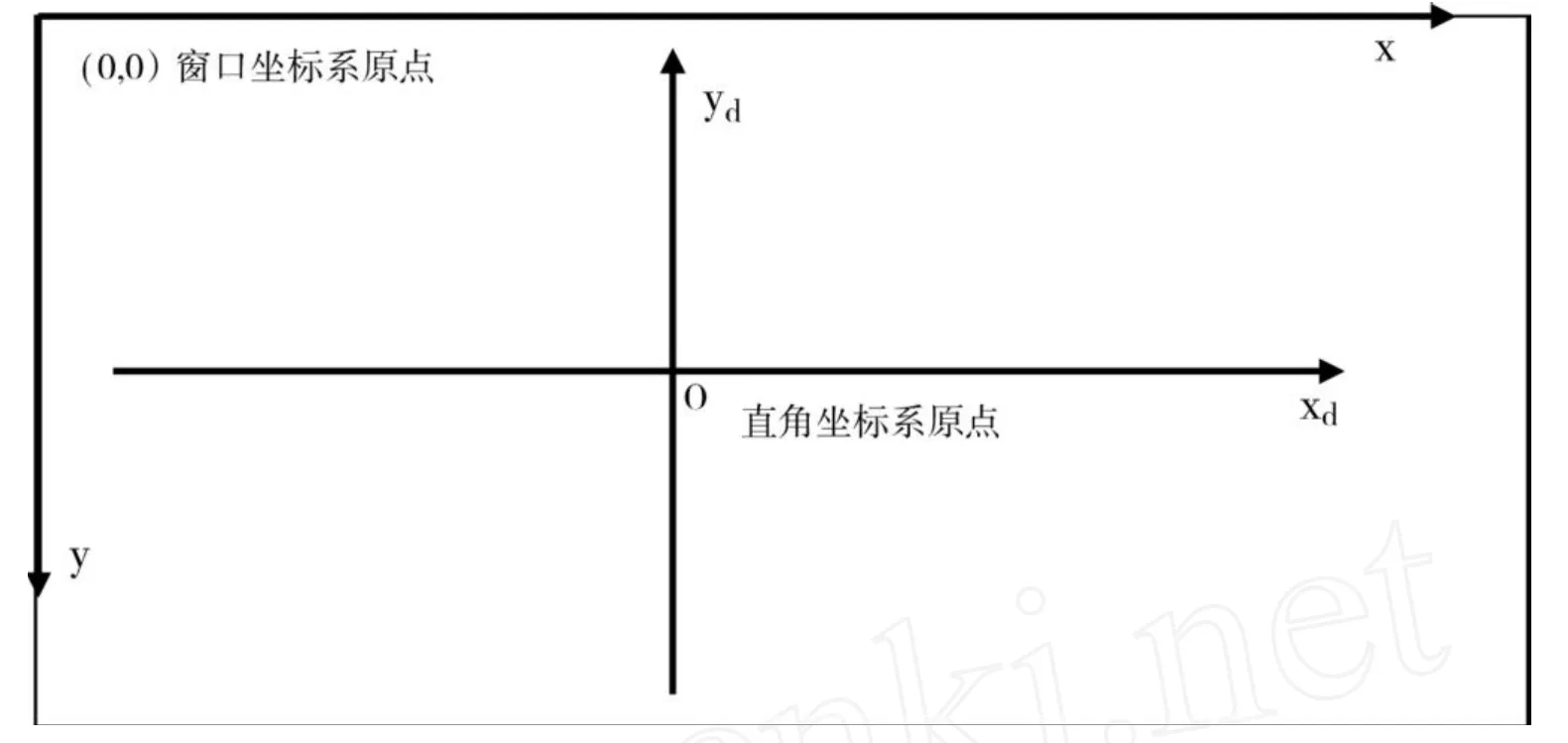
图1 Authorware窗口坐标系与直角坐标系
再次,Authorware窗口坐标系的单位长度是像素,且窗口坐标系的可视长度是一定的,它取决于窗口分辨率的大小,如窗口分辨率的大小为800×600,就表示横坐标的长度为800个像素,纵坐标的长度为600个像素.而直角坐标系的单位长度是可以根据需要人为设定的,其坐标轴是可以无限延长的.制作图形演示课件一个重要的参量就是可视长度,程序中一切用于显示的运算结果 (诸如函数的曲线、图形的位置等)都希望限制在可视长度范围内,从而使运算结果要说明的数学问题能够完整反映在演示窗口上.因此,为了显示的需要,在直角坐标系、极坐标系下运算的结果都要向Authorware演示窗口坐标系转换.
2 直角坐标系向窗口坐标系的转换
其变换的基本原则是将窗口坐标系看作是一个绝对坐标系,把直角坐标系看作是在窗口坐标系下经过一系列变换后所得到的相对坐标系.函数的变换也受这一系列坐标系变换过程的制约.其基本过程可以分为三个步骤 (以直角坐标系的原点在窗口中心为例):
第一步:平移 设窗口坐标系坐标变量为 x、y,窗口分辨率为 (i×j).将窗口坐标系平移到窗口中心,创建一个新坐标系Ⅱ,其坐标变量为 x1、y1,那么显然有
x1=x-i/2
y1=y-j/2
公式中的j/2和i/2是求得窗口坐标轴长度的一半.这个坐标系还不是直角坐标系,其坐标系统的纵坐标是向下递增的.
第二步:翻转 将坐标系Ⅱ以坐标轴 xd为基准进行上下翻转,使坐标系统的纵坐标向上递增,形成新坐标系Ⅲ,其坐标变量为 x2、y2,那么
x2=x-i/2
y2=- (y-j/2)
这个坐标系就是坐标原点在窗口中央的直角坐标系.
设该直角坐标系函数公式为:y2=f(x2),
则窗口坐标系下函数公式变换为:y=-f(x-i/2) +j/2.
第三步:缩放 由于窗口坐标系的横、纵轴长度和单位是一定的,所以经常会出现函数曲线图像超出窗口显示范围或函数图像过小的现象,这不利于窗口上的教学演示.为了取得较好的教学演示效果,还应进一步对坐标系进行缩放变换,形成新坐标系Ⅳ.
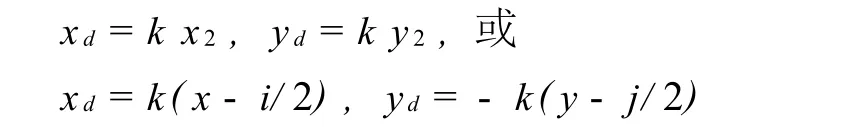
设k为描述坐标系缩放程度的参量,设 xd、yd为坐标系Ⅳ的坐标变量,那么这个坐标系就是缩放后的坐标原点在演示窗口中央的直角坐标系.改变k值就可以改变坐标系坐标变量值的缩放程度.
根据上述进行推广,设直角坐标系的原点在窗口坐标系中的坐标为任意点 (x0,y0),那么
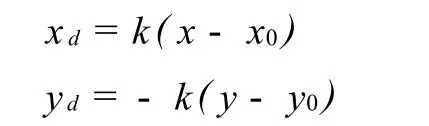
如果在直角坐标系中函数公式为:

则在窗口坐标系下函数公式为:

编程者应根据公式 (2)来编制程序,绘制出实际函数图像,但观察者感受到的是直角坐标系函数公式 (1)的图像.
通过上述平移、翻转和缩放三个步骤,就可以将直角坐标系中的函数公式 (1)变换成窗口坐标系中的函数公式 (2)了.坐标系变换的过程如图2所示.
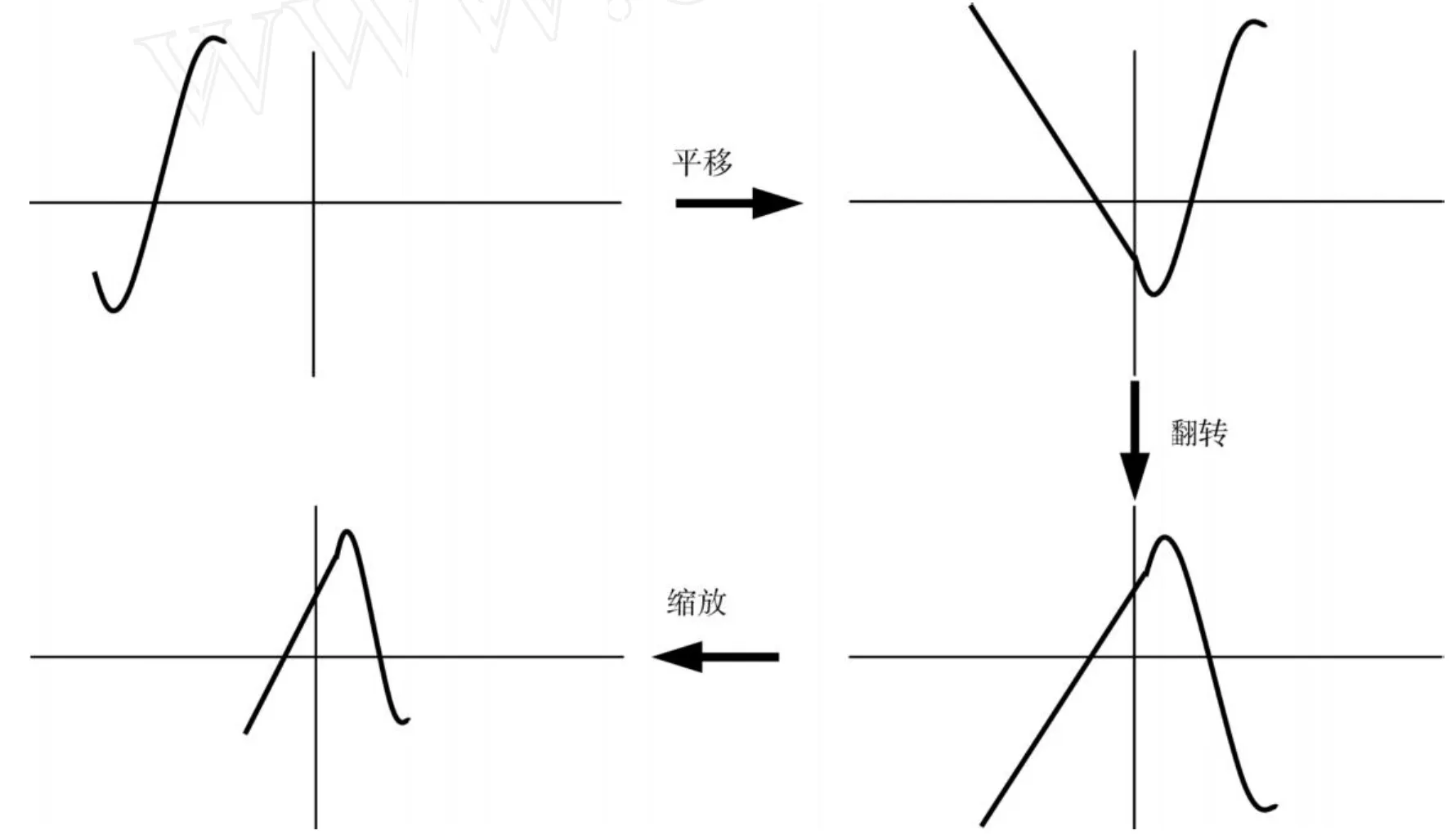
图2 图示坐标系转换的过程
例如画正弦曲线,程序代码如下:
x0:=400 ------定义直角坐标系原点x0,y0)
y0:=300
a:=350
b:=200
SetLine(2)
Set Frame(1,RGB(0,0,0))
Line(2,x0-a,y0,x0+a,y0) ------画直角坐标轴X轴
Line(2,x0,y0+b,x0,y0-b) ------画直角坐标轴 Y轴
Set Frame(TRUE,RGB(255,0,0)) ------设置绘制的正弦曲线为红色
repeatwithx:=-2*Pi*50to2*Pi*50 ------循环画线
y1:=SIN(x/50)
yw:=SIN((x+1)/50)
Line(2,x+400,300-50*y1,x+400,300-50*yw) ------画线
end repeat[2]
解释:函数曲线的绘制大多是先将函数自变量的连续数值均匀分割,取出均匀的分立值,与其对应的各个因变量组成一对对的坐标值,然后利用直线绘制函数连接相邻的坐标点,最后这些直线连接起来的宏观效果就成为一条函数曲线.这个例子正是如此,同时它也用到了直角坐标系向窗口坐标系的转换技术,该程序定义窗口大小为800*600,将直角坐标系的原点设在窗口中心,坐标为 (x0,y0),显然x0=400,y0=300,对于y=sin(x)在直角坐标系下几个坐标值,如(-2∏,0),(-3∏/2,1),(-∏/2,-1),(∏/2,1),(3∏/2,1)五个点坐标,再向窗口坐标系转换过程中,首先将坐标缩放50倍,得么 (-100∏,0),(-75∏,50),(-25∏,-50),(25∏,50),(75∏,5),然后代入公式xd=x-x0,yd=-y+y0求得在窗口坐标系的坐标 (x,y),分别为 (400-100∏,300),(400-75∏,300-50),(400-25∏,300+50),(400+25∏,300-50),(400+75∏,300+50),经过这样的转换在窗口坐标系下看到的正弦曲线就和在直角坐标系下看到的正弦曲线一样了.绘制出来的效果如图3所示.函数图像绘制中的一些复杂的数学公式都可以通过上面的方法完成其数学公式的坐标系转换.

图3 正弦曲线
3 极坐标系向窗口坐标系的转换
对于使用极坐标绘图的情况,操作的方法是先利用极坐标方程 r=f(θ),由极角θ算出极径r,然后使用参数方程:
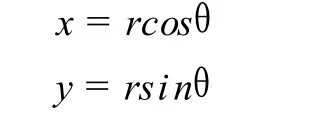
换算成直角坐标,最后再转换为窗口绝对坐标,最终绘图是使用窗口绝对坐标进行的[3].
设窗口坐标系的坐标为 x、y;转换坐标系的原点在窗口坐标系中的坐标为 x0、y0,极坐标的坐标变量为 r和θ
那么,根据前面推导的结果,可以得出:
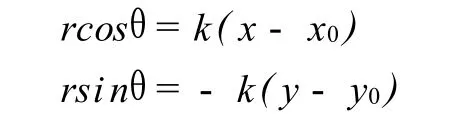
继续推导,可以得出:
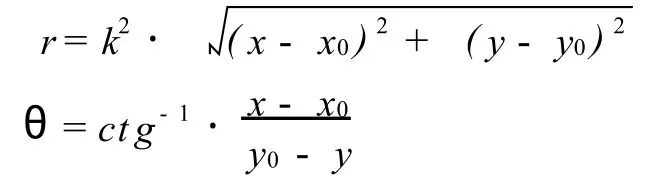
总之,所有教学课件中窗口展示的函数及其图像对于观察者来说大都是相对于直角坐标系的,但程序中Authorware却只认识窗口的绝对坐标系,所有基于程序的函数都是在窗口绝对坐标系中绘制的.因此需要将直角坐标系中所表现的图像函数根据上面的转换公式变换为窗口坐标系下的图像函数,这样才能使观察者感受到正确的图像.
[1] 牟奇春,普敏.多媒体软件开发 [M].西安:西安电子科技大学出版社,2007:1-60
[2] 朱仁成,于秋平.Authorware 7多媒体制作课堂实训 [M].西安:西安电子科技大学出版社,2006:20-96
[3] 钟玉琢.多媒体计算机技术基础及应用 [M].北京:高等教育出版社.1999:52-83
