方钢管混凝土柱抗震性能影响因素的研究

郑 杰,刘继明,毛林涛,周 飞,纪荣荣

(青岛理工大学土木工程学院,山东青岛 266033)

方钢管混凝土柱抗震性能影响因素的研究

郑 杰,刘继明,毛林涛,周 飞,纪荣荣

(青岛理工大学土木工程学院,山东青岛 266033)

确定了方钢管混凝土中钢材和混凝土材料的本构关系。利用有限元分析了低周反复荷载下试件宽厚比、长细比、轴压比和内部混凝土抗压强度等因素对构件抗震性能的影响。为方钢管混凝土框架柱的抗震设计提供参考,推动方钢管混凝土结构在实际工程中更为广泛的应用。

方钢管混凝土; 本构关系; 抗震性能

近年来钢管混凝土结构在我国得到了广泛的应用,方钢管混凝土是钢管混凝土结构的一个组成部分,与圆钢管混凝土结构处于同等地位。较之圆钢管混凝土结构,方钢管混凝土结构具有抗弯性能好、节点构造形式简单、外形规则等优势,在高层超高层建筑、地下结构、桥梁及港口工程等建设中得到了广泛的应用。作为组合结构,内填的混凝土改变了钢管的屈曲模式,阻止了钢管的内向屈曲,提高了钢管混凝土柱的稳定性和承载力;而外包钢管的约束作用使承载时的核心混凝土处于三向压应力状态,改善了混凝土的受压性能[1]。另外,在钢管混凝土的施工过程中,钢管还可以作为浇筑其核心混凝土的模板。就目前而言,圆钢管混凝土结构柱技术较为成熟,我国做了很多研究,也有相应的规程可以遵循,而方钢管混凝土结构的研究还不甚成熟。我国属于多地震国家之一,随着方钢管混凝土在我国地震区高层建筑中的推广应用,对方钢管混凝土结构的抗震性能进行研究显得尤为重要。

1 反复加载情况下材料的应力 -应变关系模型

1.1 钢材的应力-应变关系模型

本文在进行方钢管混凝土构件滞回性能的研究时,采用如图 1[2]所示的钢材应力-应变关系,可以较好地反映其滞回特性。循环荷载作用下钢材的本构模型是由骨架曲线和加载、卸载两部分组成,即弹性段(oa)和强化段(ab)。模型中考虑了钢材的强化作用和包辛格(Bausinger)效应,即正向屈服应力的提高会促使反向屈服应力的降低。弹性段刚度为ES,强化段刚度取0.01ES,加卸载刚度采用钢材初始弹性模量。d点的反向加载线与通过(0,-0.35)点平行于ab段直线。继续反向加载,进入软化段 de,其模量最小取值为 KS=0.1ES,继续反向加卸载过程用直线段a′c′d′来表示,其模量最小取值为KS=0.1ES。直线段de和de的模量用Eb来表示,其模量取值按式(1)确定。

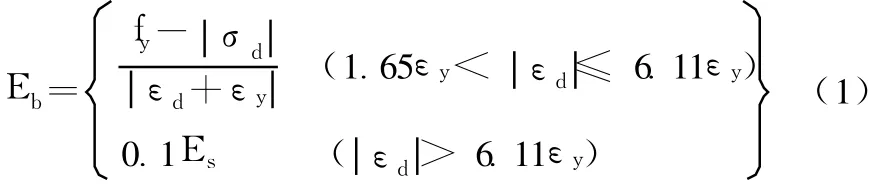
式中:σd和εd分别为软化段起始点d点和d'点的应力和应变值。

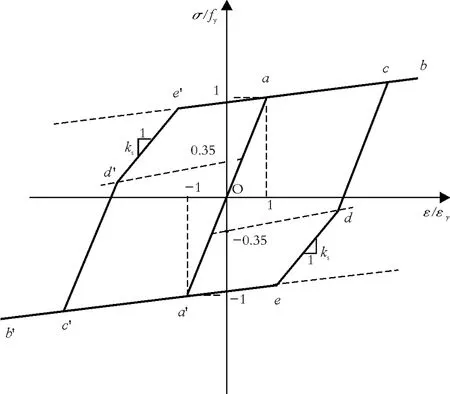
图1 反复荷载作用下钢材的应力-应变曲线

1.2 混凝土应力-应变关系模型

在反复循环荷载作用下,有关研究者进行过大量钢筋混凝土中混凝土材料应力 -应变滞回关系曲线的试验研究,发现混凝土的骨架曲线基本上接近于单向加载的应力-应变曲线,因此提出钢筋混凝土结构在反复循环荷载作用下,其混凝土材料的应力 -应变滞回关系骨架曲线可用单向加载应力-应变曲线来代替。由于对方钢管混凝土动力性能的研究开展得尚不充分,而针对其核心混凝土材料应力 -应变滞回关系的试验研究未见有报道,因此在确定方钢管混凝土的核心混凝土应力 -应变滞回关系骨架曲线时,采用单向加载的应力-应变关系曲线代替,如图2所示。E.S.Chen和0.Buyukozturk于1985年提出了混凝土边界面模型是一种功能较强的模型[3],可以用于混凝土三向受力的情况,如混凝土的非线性应力 -应变关系,循环荷载作用下的刚度退化现象等,如图 3。

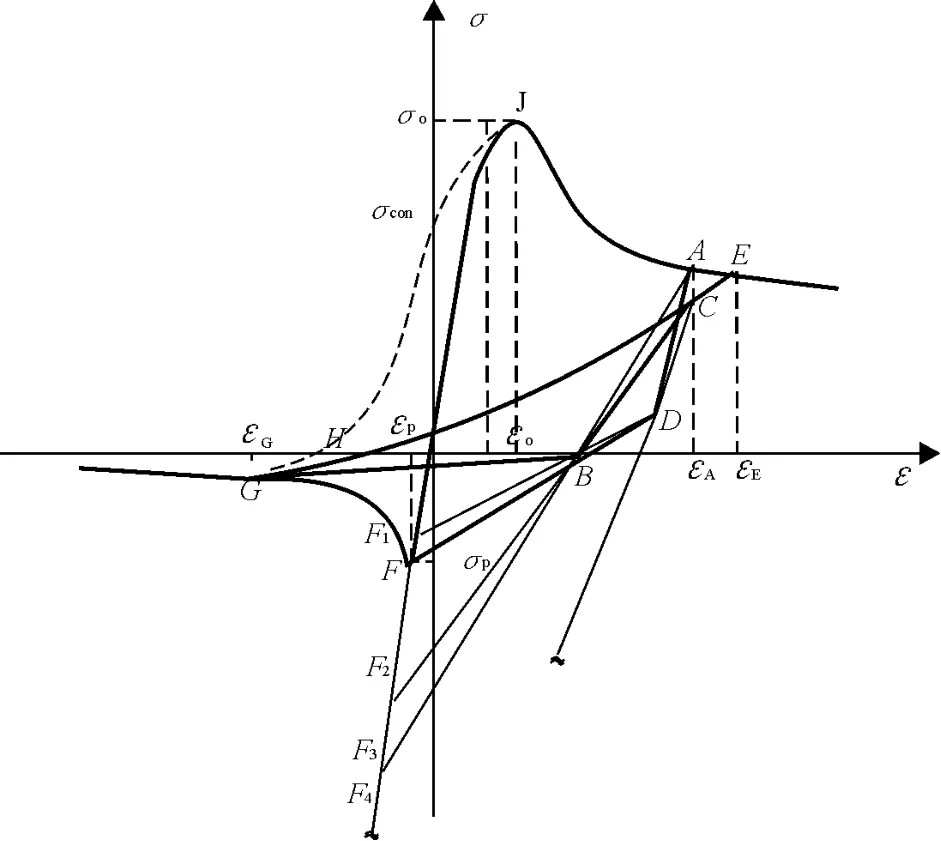
图2 混凝土的应力-应变曲线

图 3 混凝土边界面模型

受压区混凝土的应力-应变关系按式(2)确定[4]:

式中:ξ为约束效应系数;fc为混凝土圆柱体轴心抗压强度。

受拉区混凝土的应力-应变关系按式(3)确定:

σp=0.26(1.25fc)2/3;εp为峰值拉应变,εp=43.1σp(με)。

2 有限元分析

2.1 有限元研究对象

图4 方钢管混凝土模型

通过ANSYS有限元软件主要分析宽厚比、长细比、轴压比和内部混凝土抗压强度等因素对构件抗震性能的影响。由方钢管和内填混凝土组成方钢管混凝土模型如图 4所示,混凝土单元采用Solid65;钢管单元采用Solid45。混凝土材料的应力-应变关系采用Hognestad表达式,通过数据表形式输入到ANSYS中。在计算过程中首先对柱子底部施加约束,柱顶施加恒定轴压力。反复荷载通过定义荷载步的办法得以实现。

2.2 各参数对抗震性能的影响

2.2.1 宽厚比的影响

构件的宽厚比即代表了截面的含钢率,因此,宽厚比的大小直接影响试件的极限荷载。在轴压比和混凝土强度相同的情况下,宽厚比小的试件其极限强度大,宽厚比大的试件其极限强度反而小。宽厚比与含钢率成反比。随着宽厚比的减小,构件弹性阶段刚度和水平承载力都有所提高,下降段的下降幅度也略有减小。但对曲线形状的影响则不大,主要影响曲线的数值(图5)。

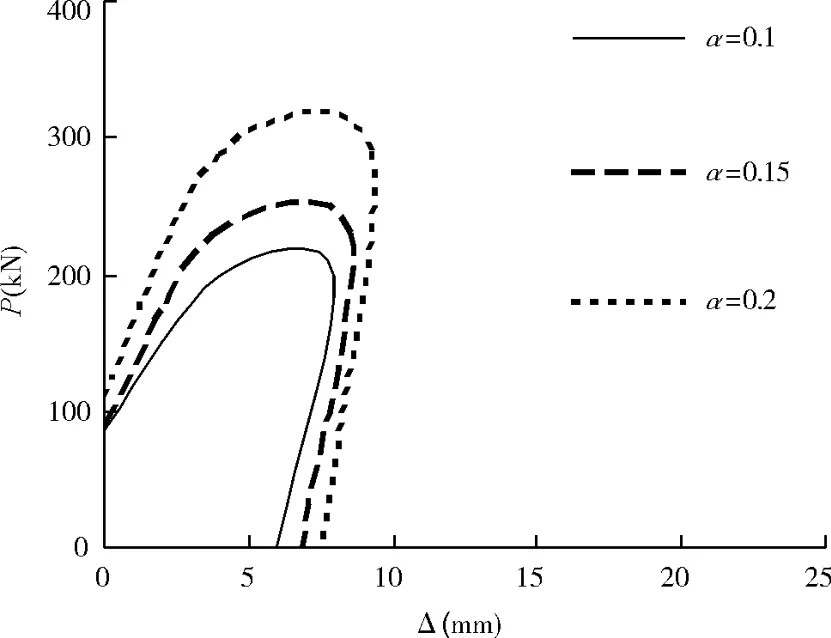
图5 含钢率对骨架曲线的影响

2.2.2 内部混凝土强度的影响

内部混凝土的强度对试件的延性有较大的影响,此外还影响试件的极限承载力。采用较低混凝土强度的试件的极限强度较低但具有良好的耗能能力和较小的强度退化;采用较高强度混凝土的试件取得了较高的极限强度,但同时它的耗能能力较差且强度退化较大。混凝土强度的改变对构件在弹性阶段刚度和水平承载力等的影响都较小,随着fck的增大,构件位移延性有减小的趋势。目前方钢管混凝土结构的应用趋向于采用高强混凝土,这就提醒我们在设计中应采取其它措施以提高其延性(图6)。

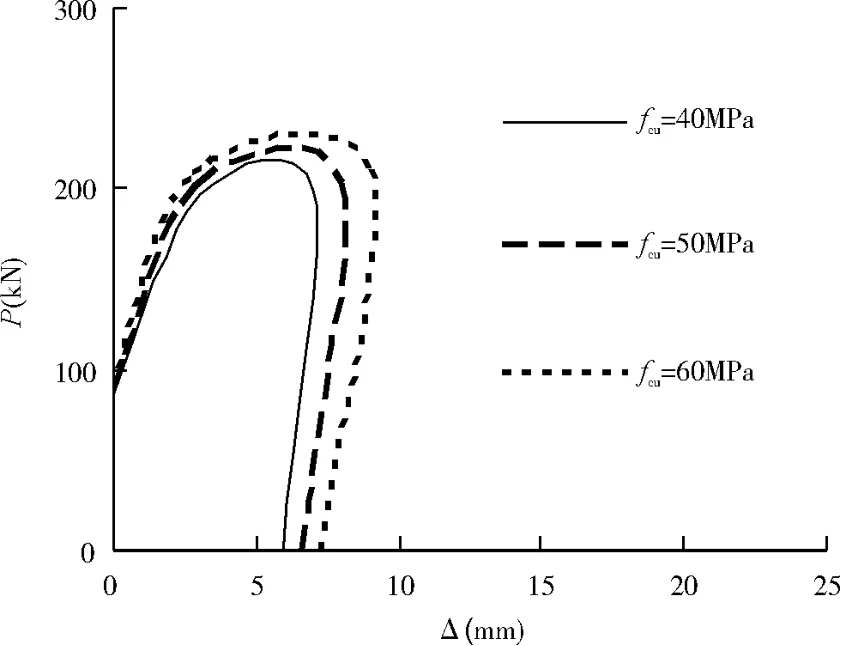
图6 混凝土强度对骨架曲线的影响

2.2.3 轴压比的影响

轴压比的大小对试件的延性和耗能能力有较大的影响且直接影响结构的抗震能力。根据参数的分析,轴压比对抗震性能的影响最大。可以看出,在宽厚比和内填混凝土强度相同的情况下,随着轴压比的增大,试件的延性和耗能能力急剧下降。轴压比是影响钢管混凝土柱延性的重要因素,轴压比越大则延性越差。轴压比对骨架曲线的形状影响较大:轴压比越大,杆件的水平承载力越小,强化阶段的刚度也越小。当轴压比达到一定数值时,其曲线将会出现下降段,而且下降段的下降幅度随轴压比的增加而增大,构件的位移延性则越来越小。另外,轴压比对曲线弹性阶段的刚度几乎没有影响,这是因为在弹性阶段,构件的变形小,P-△效应并不明显,而且随着轴压比的增大,核心混凝土受拉开裂面积会减少,这一因素又会使构件的刚度略有增加(图7)。

图7 轴压比对骨架曲线的影响

2.2.4 长细比的影响

随着长细比的增加,弹性阶段和强化阶段的刚度越来越小,水平承载力也逐渐减小。构件的长细比不仅会影响骨架曲线的数值,还会影响骨架曲线的形状(图 8)。

2.2.5 钢材屈服极限的影响

图8 长细比对骨架曲线的影响

钢材屈服极限fy对P-△骨架关系曲线的形状影响不大,但随着fy的增大,构件的位移延性有减小的趋势(图 9)。

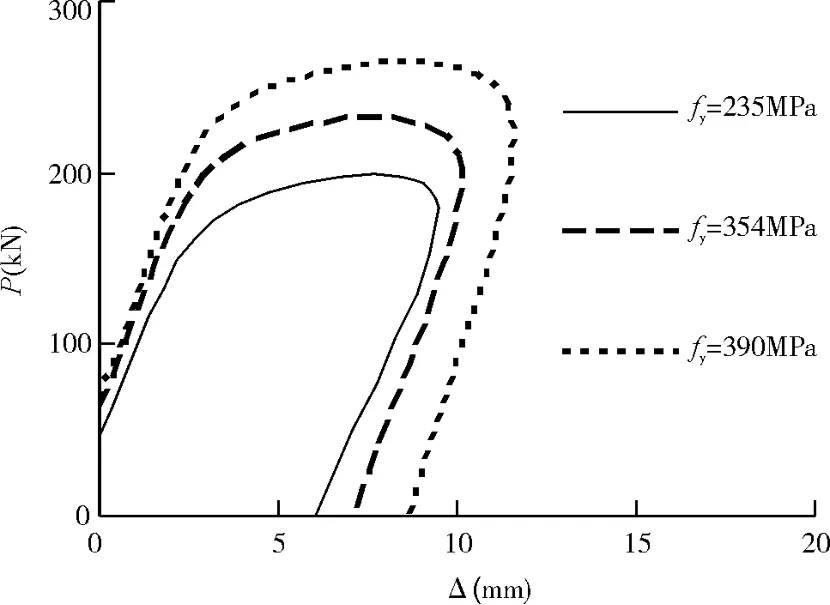
图9 钢材屈服极限对骨架曲线的影响

3 结束语

本文确定了反复加载情况下材料的应力 -应变关系模型,着重分析了低周反复荷载下试件宽厚比、内部混凝土抗压强度、轴压比、长细比、和钢材屈服极限等因素对构件抗震性能的影响。其中轴压比对方钢管混凝土结构的抗震性能影响最大,因此设计中应充分考虑轴压比的限制。目前对方钢管混凝土组合结构抗震性能的研究仍迫切需要更多试验研究,以便为更准确地建立方钢管混凝土结构性能水准提供依据。

[1] 张建辉.方钢管混凝土框架柱的抗震性能分析[D].天津大学,2004

[2] 韩林海.钢管混凝土结构—理论与实践[M].北京:科学出版社,2004:244-248

[3] 钟善桐.高层钢管混凝土结构[M].哈尔滨:黑龙江科学技术出版社,1999:46-50

[4] 韩林海.钢管混凝土结构[M].北京:科学出版社,2000:180-200

TU323.1

A

2010-02-03

郑杰(1986～),女,硕士研究生;刘继明(1963～),男,教授。