椭球约束下线性模型协方差扰动的影响分析

郝会兵,胡家喜

(孝感学院数学与统计学院,湖北孝感 432000)

椭球约束下线性模型协方差扰动的影响分析

郝会兵,胡家喜

(孝感学院数学与统计学院,湖北孝感 432000)

讨论了椭球约束下协方差阵扰动模型和数据删除模型对线性回归参数的影响问题,给出了在椭球约束下G-M模型与椭球约束下一般线性模型及在椭球约束下数据删除模型中回归参数的估计之间的关系。

椭球约束;协方差阵扰动;线性模型

1 引言

考虑 Gauss-Markov(G-M)模型

其中 X是已知的n×p列满秩的矩阵,Y为n×1观测向量,β为p×1的未知参数向量,ε为n×1随机误差向量,σ2为未知参数。文献[1-2]分别对G-M模型(1)剔除一组或若干组观测值的扰动方式作了较为详细的讨论。

当 G-M条件不满足时,模型(1)就变成一般的线性模型

其中V≥0,文献[3-5]研究了模型(2)参数的估计与回归诊断问题,得到了一系列的结果。本文讨论在椭球约束条件下满足G-M条件的回归模型

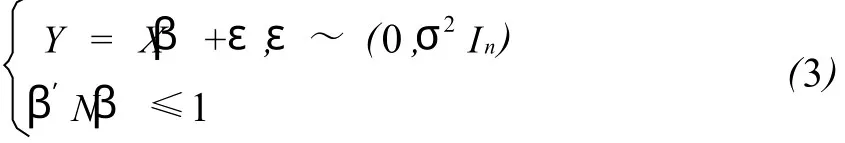
与椭球约束条件下一般的回归模型

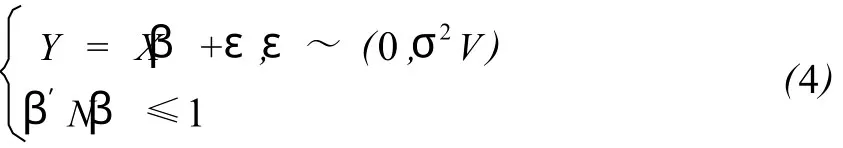
及椭球约束条件下数据删除的回归模型

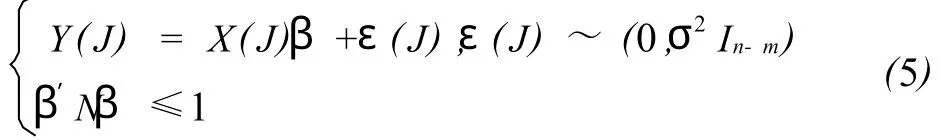
之间的关系及影响分析问题,得到一些有意义的理论结果。其中 N为大于0的 p阶对角阵,J={i1,i2,…,im}为指标集,Y(J),X(J)和ε(J)分别为模型(5)中Y,X与ε删除指标集J中各行后得到的向量或矩阵。

由文献[6-7]可知,在模型(3)中,考虑

1)若S(β)的无条件极小值满足约束条件β′Nβ=1,则该极小值就是我们的所求解。

2)若 S(β)的无条件极小值满足β′Nβ＞ 1,则极小值一定在椭球边界上取得,所以约束问题转化为在椭球面上求解的约束问题

所以实际上我们在考虑模型(3)、(4)和(5)时可将不等号改为等号来研究。

2 主要引理及结论

引理1[1]模型(1)中β的最小二乘估计^β为

引理2[3]模型(2)中β的广义最小二乘估计

引理3模型(3)中β的岭型估计为

证明由文献[6]可知

引理4模型(4)中β的广义岭型估计(V)为

证明由文献[6]可知

由上述引理,可得如下定理:

定理1假设在模型(2)中,若矩阵可逆,则

其中 T=X′X,H=X(X′X)-1X′

证明因为V=In+,由In-(In+及引理2,有

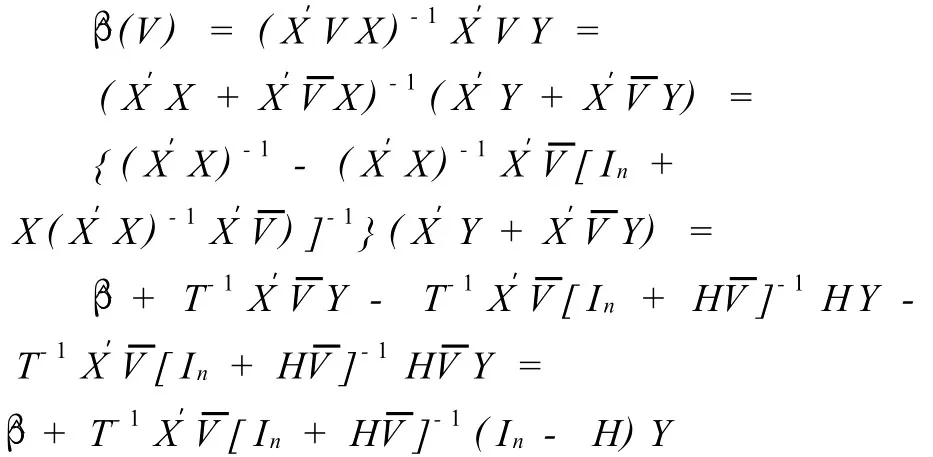
定理2模型(4)中,若矩阵可逆,则

证明因为由引理4与定理1可得

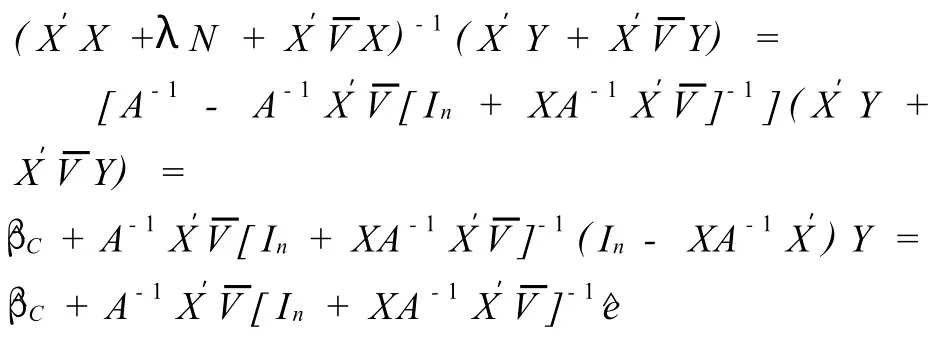
定理3模型(4)中,若V ＞0,V =In+则有

其中 dj为第j个元素为1,其余元素都是0的列向量。

证明因为

而

且

故

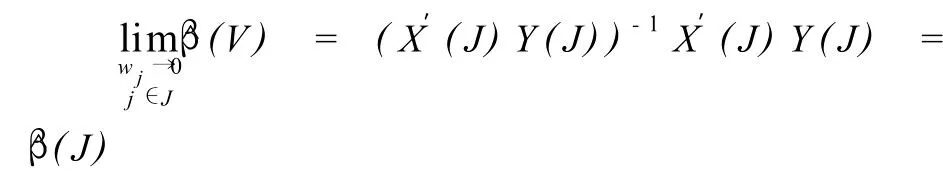
同时

所以

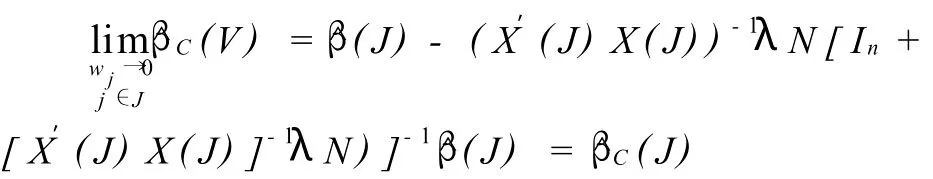
且 wj→0,j∈J时,方差扰动就等价于删除了J中的数据。

推论1模型(4)中,若

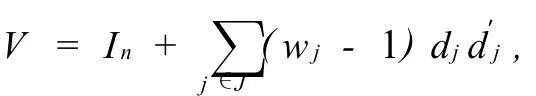
0＜ wj≤1,j∈J,则有

其中 XJ,分别是由 X,在J中各行所构成,IJ为 m 阶单位阵,

证明不失一般性,不妨设 J={1,2,…,m},则

同时有

与

所以

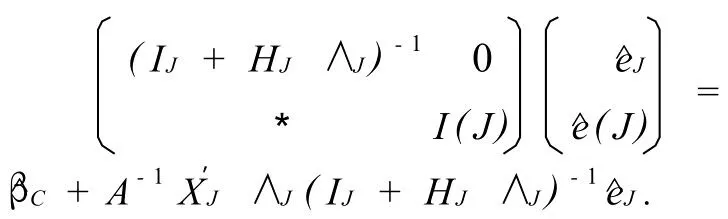
故

推论2若j∈J,则有

[1] 陈希孺,王松桂.近代回归分析[M].合肥:安徽教育出版社,1987.

[2] Cook R D,Weisberg S.Characterization of an empirical influence functions for detecting influential cases in regression[J].Technometrics,1980,22(5):495-508.

[3] 王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1987.

[4] Rao C R.Linear Statistical inference and its Applications[M].New York:1973.

[5] 朱秀娟,李宁.协方差扰动模型的影响分析[J].应用概率统计,1993,9(4):365-370.

[6] 杨婷,杨虎.椭球约束与广义岭型估计[J].应用概率统计,2003,19(3):232-236.

[7] 杨莲,杨虎.椭球约束下线性模型的[J].工程数学学报,2007,24(1):60-64.

Influence Analysis of Covariance Matrix Disturbance in Linear Model under Ellipsoidal Restriction

Hao Huibing,Hu Jiaxi
(School of Mathematics and Statistics,Xiaogan University,Xiaogan,Hubei 432000,China)

In this paper,we study the issue of the influence with covariance matrix disturbing model and data missing data.The relationship of the regression parameter among some linear models with respect to ellipsoidal restricted conditions,such as G-M model,deneralized linear model and linear model with deleted data,ismade explicitly.

ellipsoidal restriction;covariance matrix disturbance;linear model

O211.1

A

1671-2544(2010)03-0034-03

2010-04-02

郝会兵(1979— ),男,湖北云梦人,孝感学院数学与统计学院讲师,硕士。胡家喜(1957— ),男,湖北汉川人,孝感学院数学与统计学院副教授。

(责任编辑:周 游)