用Riccati方程方法解Burgers方程

范梦慧,龚伦训

(1.贵州民族学院物理与电子信息科学学院,贵州贵阳 550025; 2.贵州师范大学物理与电子科学学院,贵州贵阳 550001)

0 引 言

非线性物理现象越来越受到广大学者的关注,利用光纤研究许多非线性物理现象,寻求非线性方程的解,是一个重要的研究方向.一些新方法不断被学者们提出来,如渐进法、格林函数法、Jacobi椭圆函数展开法、特殊函数求解法等[1-4].

Burgers方程是非线性的耗散方程,其也被许多文献选为典型范例[5,6],一些学者对非线性Burgers方程的精确解做了研究[7].本文利用Riccati方程方法[8],并用数学软件Mathematica求解Burgers方程,得到了Burgers方程的冲击波解及相应的孤立波解,并利用Matlab作图对其加以说明.

1 方法简介

对于有两个变量 x和t的非线性波动方程,

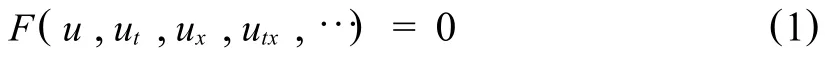
当波沿正x方向以速度c传播时,可做如下行波变换,

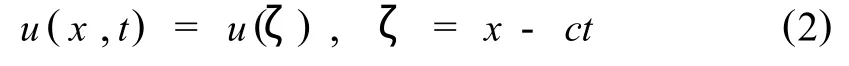
式中,c是波速.

将方程(2)代入方程(1)得到非线性常微分方程,

设方程(3)的形式解为,

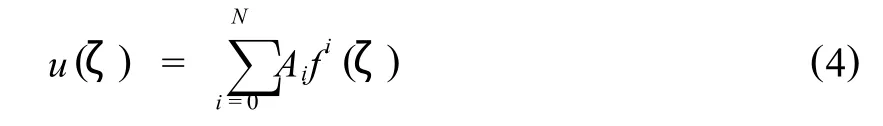
式中,Ai为待定常数,N由f(ζ)的非线性项和最高阶导数项平衡而得,并同时满足,

这里,“′”是d/dζ,r、p、q是待定常数,它们的取值确定函数f(ζ)的具体形式.

(1)当 p2-4rq＞0,且 pq≠0(或qr≠0),

(2)当 p2-4rq＜0,且 pq≠0(或qr≠0),

当然,r、p、q还可取其他不同的值,相应的f(ζ)也有其他形式的解,具体可参阅文献[7].

将式(4)、(5)代入式(3),然后合并 fi(ζ)的同类项,并令系数为零,得到系数Ai的代数方程组,解这个代数方程组可确定此系数.

2 构造Burgers方程的解

Burgers方程是非线性的耗散方程,其一般形式为[5,6],

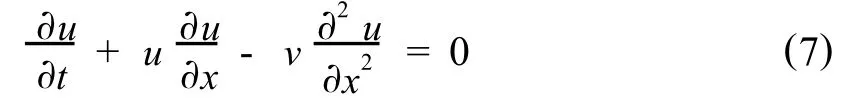
式中,v＞0为耗散系数.

设式(7)有如下形式的行波解,

把式(8)代入式(7)得,

式(9)的非线性项为,

最高阶导数项为,

根据非线性项与最高阶导数项平衡得N=1.所以式(9)的解可以表示为

把式(12)和式(5)代入式(9),再合并fi的同类项,且令前面系数为零,得到如下代数方程组,

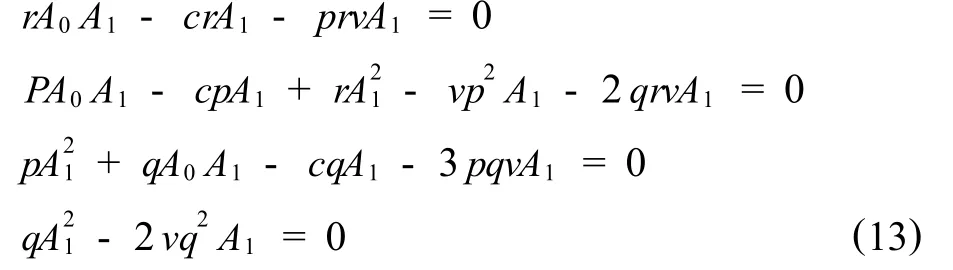
利用计算软件Mathematica求出方程组(13)的解如下,

将式(14)代入式(12),再选择合适的参数 r、p、q来确定f(ζ)的具体形式,可得到式(9)的一些行波精确解.其中,当 p-4rq＞0,且 pq≠0(或 qr≠0),A0=c+pv,A1=2qv,有,

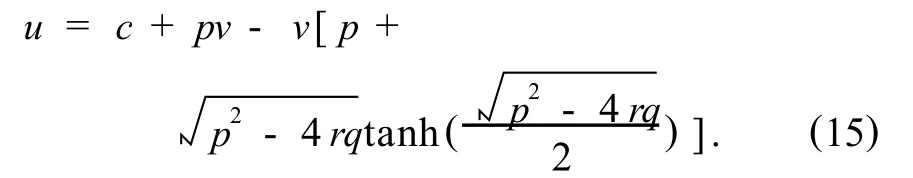
当取r=1,p=1,q=0.2,c=2,v=20,-30≤ζ≤30,用数学软件Matlab对式(15)作图,结果如图1所示.此时,图1显示式(15)是一个冲击波解.

如将 u对ζ求导数一次,得

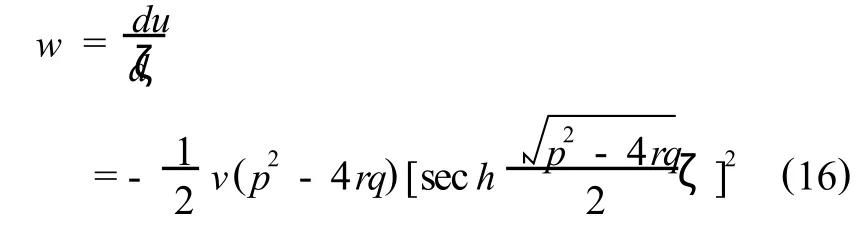
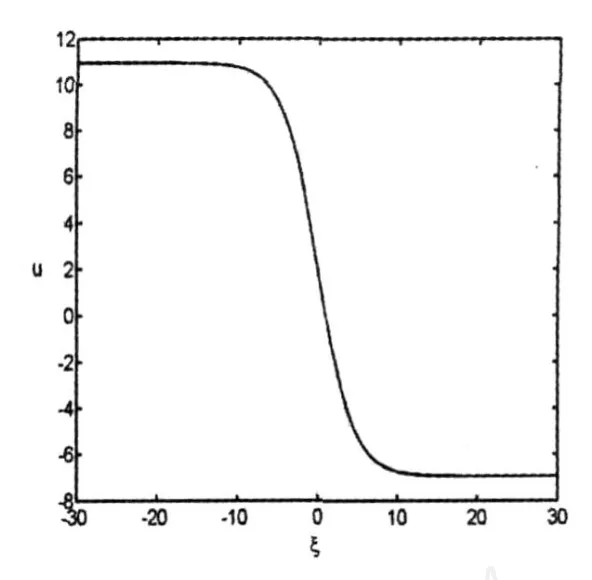
图1

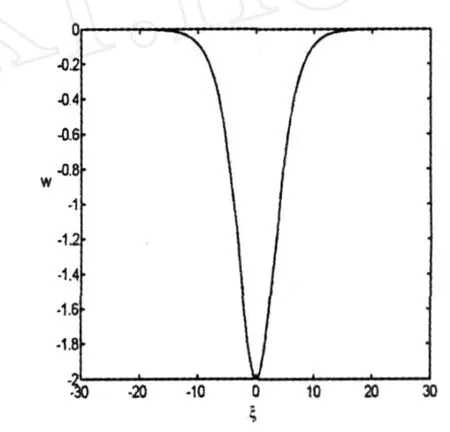
图2

3 结 论

本文采用Riccati方程方法,利用数学软件求解Burgers方程,得到Burgers方程的冲击波解和相应的孤立波解,方法简便,并绘图说明其解.此外,r、p、q还可取其他不同的值,便还能得到一些精确解,这里不一一列举.

[1]叶晓林.非线性单摆的三级近似解[J].大学物理,1993,12 (1):26-27.

[2]孙春峰.非线性单摆的格林函数解法[J].大学物理, 2004,23(1):9-11.

[3]佘守宪.非线性振动、非线性波与Jacobi椭圆函数[J].大学物理,2004,23(1):3-8.

[4]夏清华.含项非线性振子运动的研究[J].大学物理, 2005,24(4):6-7.

[5]刘式适,刘式达.物理学中的非线性方程[M].北京:北京大学出版社,2007:168-169.

[6]郭玉翠.非线性偏微分方程引论[M].北京:清华大学出版社,2008:40-43.

[7]贺 锋,赵 凡.用三角级数和Maple软件求Burgers方程的精确解[J].大学物理,2009,28 (3):8-9.

[8]Xie F D,Yuan Z T.Computer Algebra and Solutions to the Karamoto-sivashinsky Equation[J].Commun Theor Phys,2005,43(1):39-44.