有害物品运输风险度量过程中的计算误差分析

郭晓林，李 军

（1.西南交通大学 经济管理学院，成都 610031；2.成都信息工程学院 管理学院，成都 610225）

0 引言

由于有害物品的普遍使用，其运输问题也成为一个常见的问题。有害物品或称危险品包括爆炸物品、气体、可燃液体和固体、氧化物、有毒或传染性物质、放射性物质、腐蚀性物质和有害废料等（郭晓林等，2006）。对于大多数工业社会的成员来说，没有有害物品的生活是不可想象的。遗憾的是，大多数的有害物品不是在生产地使用，它们需要运输相当长的距离。据估计，在美国每年有害物品的运输量将达到15到40亿吨，公路上行使的车辆中每十五辆就有一辆是运输有害物品的（Erkut和 Verter,1998）。

有害物品运输与其它物品运输的区别在于运输过程中事故发生的相关风险。有害物品会对环境和人类健康产生极大的伤害，因为接触到他们的有毒化学成分将导致植物、动物和人的损伤甚至死亡。这种危险已被社会所认识，很多情形下，对有害物品的流动有着严格的规章制度管理。因而有害物品的承运人比其它一般物品的承运人在发生事故方面有着更好的记录。不过，虽然发生事故的情况相对较少，但事故还是时有发生。

正因如此，有害物品运输仅以成本最小化为目标通常是不合适的。早在上世纪80年代人们就已经意识到这一点，并明确提出在对有害物品运输线路进行安排时，必须考虑路径运输风险[2]。事实上，我们常常将有害物品运输问题归结为以运输成本和运输风险为目标的双目标问题。因此，如何合理度量运输风险便成为求解有害物品运输问题的基础。也正因如此，以Erkut为代表的大批学者对如何度量有害物品运输风险进行了大量的研究，并提出了多个度量模型(Erkut&Ingolfsson,2005），其中应用较为广泛的是所谓的传统风险模型。在有害物品运输风险度量过程中，为了计算的方便，都不同程度地作过一些假设或近似处理，但这种假设或近似处理是否会导致计算结果的不可信或无法应用却没有进行专门的讨论。本文拟在回顾传统风险模型的基础上，分析使用这一模型进行风险度量时可能产生计算误差的主要情形，并应用数字例子，就其误差对运输风险的计算结果的影响程度进行评估。最后，还将讨论几种常用的风险度量模型存在的计算误差情况。

1 有害物品运输传统风险模型回顾

有害物品运输风险就是所谓路径运输风险，一般而言，一条路径由若干边组成，而每一边又由若干基元路段构成。因此，Erkut和Verter（1998）从基元路段风险开始，系统地对路径运输风险进行了分析和总结。

1.1 基元路段风险

所谓的基元路段是指一定长度（如1公里）的路段。根据传统风险的定义方法，运输有害物品通过基元路段d的风险可以表示为：

其中：pd表示运输有害物品通过基元路段d时发生事故的概率；Cd表示基元路段d两侧一定区域内的人口数。

1.2 边的风险

在基元路段运输风险基础上，可以继续讨论有害物品运输网络中一条边的风险计算问题。路网中一条边是由n条基元路段的组成，且所有基元路段具有相同的事故发生概率p以及影响人口C。运输工具要么在第一公里内发生事故，要么将安全到达第二公里。如果到达第二公里内，要么在第二公里内发生事故，要么将安全到达第三公里，依次类推。假设一旦发生事故运输行为便结束。那么此边上的运输风险可以表示为：

显然，若给定p,n,C,很容易计算出（2）式的值，并将其作为边的属性值（权）运用于路径选择问题。但是，采用以下近似可以大大简化（2）式的计算：

这一近似有其合理的依据，因为p几乎是百万公里分之一的量级。作了此近似后，在此边上运行的运输风险则变为：

如果记pi=边i上发生事故的可能性=（边i中单一基元路段上发生事故的可能性）×（边i含有的基元路段数）；Ci=沿着边i的危险圈中的人口数。那么边i上的运输风险可以表示为：

1.3 路径风险

用（1）～（5）式表示了基元路段以及边上的运输风险后，接下来要讨论的是，怎么表示从起点到终点的整条路径的风险。由于路径可以看作是若干边组成的集合，车辆在路径上的行驶则可以看作是做一系列的随机试验。那么，与此运行相关的期望后果，也就是路径运输风险，可以表示为：

为了简化计算，作类似于（3）（也即 1-pi≈1，对于任意 i）的假设。这样，沿着路径r运输有害物品的运输风险可以表示为（Erkut和 Verter,1998）：

2 路径运输风险度量中的误差分析

在路径运输风险度量过程中，为了计算的方便，常常会采用一些隐含假设或近似处理。这些做法将给计算结果带来一些误差是显而易见的，但是是否会导致计算结果失去意义却需要进行详细分析后才能判断。

2.1 影响后果误差

在应用（7）式进行路径风险度量时，对事故影响后果的估计通常是在确定影响区域面积的基础上乘上相应的人口密度得到。以爆炸物品运输为例，对事故影响后果的估计首先需要根据爆炸物品的运载量确定一旦发生事故时的影响半径，然后根据人口普查数据，找出路段所在行政区的人口密度，最后用影响区域的面积乘以人口密度便得出事故影响后果。由于人口密度是由人口普查得出的人口总数除以该行政区域的面积得出，没有考虑人口的具体分布状况。这有可能导致某些路段的影响后果过分高估或低估，比如有可能出现在某些路段的影响半径范围内根本无人居住，但其影响后果仍按人口密度乘以影响区域面积来计算，这显然大大高估了这一路段的影响后果。另外，这一处理方式也默认影响区域内的人口（无论离事故中心远还是近）将有相同的受伤害的概率，显然也不完全符合实际情况。这也会导致对影响后果的高估或低估。对整个路网而言，我们无法建立一个包含每一路段的任何影响半径内所覆盖的实际人口数的数据库，也无法确定每一路段附近的人口分布状况。因此，这种处理虽然与实际情况存在一定的误差 (有时这一误差可能很明显)，但这是使风险度量得以继续进行的无奈选择。

导致影响后果估计误差的另一情形是：由于上下班等缘故产生相当的人口短期迁移，使得一定区域内精确人口数与具体的时间密切相关。因此，如果有害物品运输是安排在白天通过某一地区，那么利用人口普查数据估计风险圈内风险人口也会出现误差，这是数据的可得性导致的局限。因而，如果白天的人口数据可以获得，或者它们可以被精确估计，那么，当处理白天有害物品运输问题时，就应该用它们来代替人口普查的数据。如果有害物品运输可能发生在白天或者晚上，那么，最好使用白天和晚上人口的加权综合或者其最大值。对于这一情形，还引出了具有事变特性的有害物品运输问题。魏航（2006）等人对此作了比较详细的研究。

2.2 近似计算误差

正如Erkut和Verter(1995）指出的那样，几乎所有有关有害物品运输的研究都使用了与（3）式类似的近似处理，但是并不一定对此进行了明确的说明。因为采用此近似处理后，能顺利使用最短路算法求解风险最小化问题，从求解实现的角度看，近似处理的优点是显而易见的，它能使问题变得易于处理。但是，利用这一近似将给其解带来的误差也是事实。这种近似处理由于忽略风险表达式中的高阶项会高估事故发生的概率，并且，行驶路线越长，高估的程度越高（Erkut和Verter,1998）。现在我们要考虑的是这种高估是不是足以使利用近似得出的结果无效，或者说误差是不是在我们可接受的范围内。

我们可以通过一个数字例子来观察一下这个问题的答案。考虑一条含有n个基元路段的边。假设每一基元路段上发生事故的概率均为pi=p（对于所有i），事故发生后的影响后果Ci=C（对于所有i）那么n公里的边上的运输风险为：

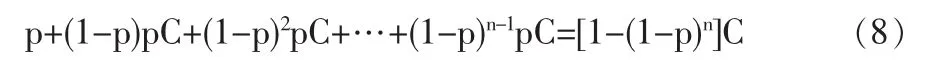
如果使用（3）式进行近似计算，那么n公里的边上的运输风险为：

此计算过程中的绝对误差Ea为：

相对误差Er为：

表1计算了基元路段数分别为 500、1000、1500、2000、2500、3000，事故发生概率分别为 1/10000（每公里）、1/100000（每公里）、1/1000000（每公里）、1/10000000（每公里）时，由于近似计算所导致的边运输风险的相对误差。从表1可以看出，基元路段上发生事故的概率越小，近似计算导致的（相对）误差也越小；边所含基元路段数量越多，近似计算所导致的（相对）误差也越大。表1中的第2列数据意味着当事故发生概率为1/10000（每公里）时，边运输风险的实际值与近似值之间的相对误差随边所含基元路段数量的不同在2.454%至13.602%之间变化，这一误差水平是值得我们注意的。值得庆幸的是，实际的事故发生概率比1/10000（每公里）要小得多，如美国伊利诺伊州的这一数据为5.91×10-6（每公里）(Harwood etal,1993)。而可能的边的长度可以从平均运距来推断，出于成本及运输时间方面的考虑，公路运输通常在中短距离市场有优势。2007年我国公路运输的平均运距仅为69公里 （漆先望等，2009）；美国的这一数据为289英里（张剑飞等，2005）。也就是说，实际的边的长度不会超出表1中的最大边长度。这样，当基元路段事故发生概率不超过1/1000000（每公里）时，边运输风险的实际值与近似值之间的相对误差则在0.002%至0.15%之间变化。这一误差水平，在大多数情况下是可以接受的。由于路径运输风险是边运输风险的和，两者的相对误差水平应在同一数量级水平，因此，当边运输风险的计算误差在一个可以容忍的范围内时，路径运输风险的计算误差也将在一个可以容忍的范围内。

表1 近似计算边运输风险引起的相对误差

2.3 离散化处理误差

在讨论近似计算误差时，我们注意到了近似计算所产生的误差并不像我们想象的那么严重。但是，在边的事故发生概率计算中，还存在另外一种误差：事故过程的离散化处理。有害物品运输活动被看作随机试验，边上有多少基元路段，试验就被重复做多少次。但是，事实上，有害物品运输是连续活动。当基元路段为1公里时，m公里长的边含有m条基元路段，该边上的运输风险为：

假设希望通过使用更短的基元路段使行程更细化来提高运输风险计算的精确度，把原有的基元路段再分成k段，则每一段上事故发生的可能性则为p/k，m公里长的边上的运输风险则为：

对这个级数取极限,则有：

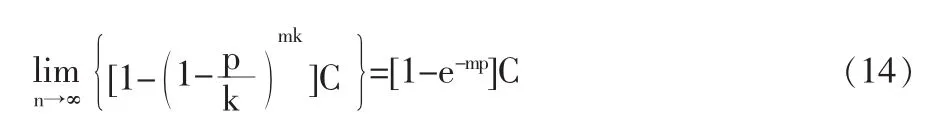
从计算结果来看，基元路段为1公里时m公里的边上的运输风险与基元路段为无穷小时m公里的边上运输风险有所不同，其相对误差可表示为：

表2中计算出了基元路段为1公里和无穷小时一定长度边上运输风险的计算误差。

表2 基元路段为1公里和无穷小时一定长度边上运输风险的相对计算误差

从表2可以看出，边越长，离散化不同处理导致的相对计算误差越小；事故发生概率越小，相对计算误差也越小。尽管相对计算误差受边长和事故发生概率的影响，但其大小主要由事故发生概率决定，而对边长的变化不够敏感（如当每公里事故发生概率为1/1000000时，相对误差在6位小数上是相同的）。总体看来，表中最大的相对误差仅为0.004988%，而当每公里事故发生概率落在1/100000和1/10000000时，相对误差更是小于0.0005%。由此可以看出，对于边运输风险的计算问题，不同的离散化处理方式不会导致明显的计算误差。

3 几种常用模型的计算误差分析

以上分析的是传统风险模型的计算误差问题。事实上，常用的运输风险度量模型除了传统风险度量模型外，还有以下几种(Erkut和Ingolfsson,2005）（见表3）。在这些模型中同样存在不同程度的计算误差问题。为了叙述的方便，把由于影响后果度量的不精确而导致的路径风险计算误差称为第1类误差；由于对事故概率进行近似计算引发的路径风险计算误差称为第2类误差；而由于离散化处理引发的路径风险计算误差称为第3类误差。

表3 几种常用风险度量模型

其中，pi=边i上发生事故的可能性；Ci=沿着边i的危险圈中的人口数；Di=沿着边i的矩形区域中的人口数；q、k分别为决策者的风险态度参数。

由于模型Ⅰ仅考虑到沿路径r的影响人口，没有考虑各边上发生事故的概率，因此，该模型只可能出现第1类计算误差，而不会出现第2类和第3类计算误差。

而模型Ⅱ与模型Ⅰ则刚好相反，由于该模型不含有影响人口这一变量，因此只会出现第2类和第3类计算误差，而不会出现第1类计算误差。对于此模型中，第2类和第3类计算误差的大小可以用类似于前述分析方法来估计。经过分析不难知道，此模型中第2类和第3类计算误差的大小与传统风险度量模型的完全一致。

对于模型Ⅲ，由于模型中含有风险态度参数q,出于对大事故规避的考虑，此参数往往大于1，这使得各边对应的影响后果在路径风险度量中所起的作用更大。从而导致由于影响后果度量的不精确引发的路径风险计算误差比采用传统风险模型时更大。而对于第2类和第3类计算误差，此模型中一定存在。若视Ci、q为常数，其大小与传统风险模型中的计算误差也是一致的。

几种常用风险度量模型计算误差情况见表4。

表4 几种常用风险度量模型计算误差情况

表4中，第1类误差=由于影响后果度量的不精确而导致的路径风险计算误差；

第2类误差=由于对事故概率进行近似计算引发的路径风险计算误差；

第3类误差=由于不同的离散化处理引发的路径风险计算误差；

显著=误差水平比传统风险模型中的误差水平更高；

相当=误差水平与传统风险模型中的误差水平相当。

4 结论

在应用传统风险度量模型对有害物品运输风险进行度量时，有可能在影响后果计算、近似计算、离散化处理等方面出现计算误差。如果人口数据信息足够充分，那么应该用精确的人口数据取代人口普查数据。对事故发生概率采用近似计算也会导致一定的计算误差，但由于有害物品运输事故发生概率通常非常小，使得这种误差的相对比率往往事实上会在一个可以容忍的比较小范围内。不同的离散化程度处理虽然也会产生一定的计算误差，但是这种误差比近似计算产生的相对误差还要小得多，因此我们有足够的理由忽略它。总之，对影响后果、近似计算以及离散化的不同处理方式，都会产生一定的计算误差。影响后果估计的误差有可能比较明显，且纠正成本较高。而后两类误差实际上很小，不会影响计算结果的应用。

对于其它几种常见的风险度量模型，其计算误差的情形与传统风险度量模型基本一致。影响后果估计导致的误差（如果存在的话）通常比较显著，而事故概率的近似计算以及不同的离散化处理导致的误差则会在一个可以容忍的范围内。

[1]Erkut,E.,Verter,V.Modeling of Transport Risk for Hazardous Materials[J].Oper.Res，1998，46.

[2]Erkut,E.,Ingolfsson,A.Transport Risk Models for Hazardous Materials:Revisited[J].Operations Research Letters,2005，33.

[3]Glickman,T.S.Benchmark Estimates of Release Accident Rates in Hazardous Materials Transportation by Rail and Truck[J].Transportation Research Record,1988，1193.

[4]Harwood,D.W.,Viner,J.G.,Russell,E.R.Procedure for Developing Truck Accident and Release Rate for Hazmat Routing[J].Journal of Transportation Engineering,1993，119(2).

[5]郭晓林，李军.基于事故分级的有害物品运输路经风险度量模型研究[J].中国安全科学学报，2006，16(6).

[6]国家法制办.淮安市人民检察院诉康兆永、王刚危险物品肇事案[EB/OL].http://www.chinalaw.gov.cn/article/fgkd/xfg/aljx/200904/2009 0400132325.shtml，2009.

[7]漆先望等.扩大铁路南通道开辟对外开放捷径[EB/OL].www.sc.cei.gov.cn/DOWNLOADS/10037.doc，2009.

[8]魏航.时变条件下有害物品运输的路径选择研究[D].成都：西南交通大学，2006.

[9]张剑飞，袁宇等译.运输管理[M].北京：机械工业出版社，2005.