关于正定矩阵的广义几何平均不等式

王子瑜

（1.华东师范大学，上海 200241；2.铜陵学院，安徽 铜陵 244000）

关于正定矩阵的广义几何平均不等式

王子瑜1，2

（1.华东师范大学，上海 200241；2.铜陵学院，安徽 铜陵 244000）

文章研究正定矩阵的相关不等式，利用单位正定线性函数性质，得到不等式：，进一步推出一系列矩阵的广义几何平均不等式，同时推广了逆Cauchy-Schwarz矩阵不等式和逆H lder矩阵不等式。

单位正定函数；正定矩阵；Kronecker积

定义1.1 设A为n阶半正定矩阵，A的特征值为λ1≥λ2≥…≥λn，f为包含的 λ1，λ2，…，λn的连续函数，A＝U*diag（λ1，λ2，…，λ）nU，定义

一、引言

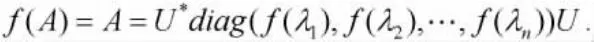
二、主要结论

［1］Rajendra Bhatia.Matrix Analysis[M].New york:Springer-Verlag,1997.

［2］Jean-Christoph Bourin,Eun-Young Lee,Masatoshi Fujii.A matrix reverse Holder inequalitity[J].Linear Algebra and its Application,437(2009)2154-2159.

［3］Tukayuki Furuta.Operator inequalities associated with A logA via Specht ratio[J].Linear Algebra and its Application,375(2003)251-173.

［4］Eun-Yong Lee.A matrix reverse Cauchy-Schwarz inequality[J].Linear Algebra and its Application,430(2009)805-810.

［5］Masatoshi Fujii,Eun-Young Lee.A difference counterpart to a matrix H觟lder inequality[J].Linear Algebra and its Application,432(2010)2565-2571.

［6］C.-K.Li,R.mathias.Matrix inequalities involving a positive linear map[J].Linear Algebraand its Application.41(1996)221-231.

［7］XingzhiZhan.MatrixInequlities[M].Berlin:Springer-Verlag,2002.

O151.21

A

1672-0547（2010）04-0064-02

2010-07-11

王子瑜(1966-)，男，安徽池州人，铜陵学院数学与计算机科学系副教授，研究方向：矩阵理论及其应用。