抽象积分方程的加权伪概自守解

张荣娟,褚衍彪,宋晓秋

(中国矿业大学 理学院,江苏 徐州 221116)

本片篇章讨论了如下抽象积分方程的加权伪概自守解的存在性与唯一性

其中 t∈R,f,g,h1,h2,C:R→R是连续的函数,Q:R×R×R→R也是连续的.

1.准备工作

对每个 t∈R成立,且

对于每个 t∈R成立.

记 R到 X的概自守函数的集合为 AA(X).

定义 1.2 函数 f∈C(R×X,X)称为概自守的,若对任意序列存在 {αn}与函数 g:R×X→X,使得

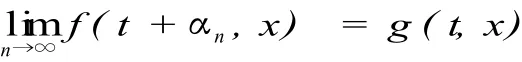
对每个 t∈R成立,且

对于每个 t∈R成立.

记 R×X到 X的概自守函数的集合为 AA(R×X,X).

引理 1.3[1]如果取函数 f∈AA(X)的上确界范数,即 ‖f‖AA(X)=‖f‖, 则为 Banach空间.

引理 1.4[1]如果 f:R→X为概自守函数,则 f有界.

引理 1.5[2]设 f∈AA(R×X,X),若存在常数L＞0,对一切 x,y∈X和 t∈R,使得 f满足 L ip sch itz条件

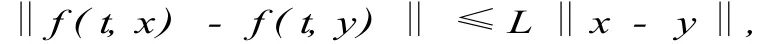
如果 h∈AA(X),则 f(t,h)∈AA(X).

记 U为ρ:R→(0,∞)在 R上局部可积,且ρ＞0的函数的集合.对任意的ρ∈U,给定r＞0,设

Ub={ρ∈U∞:ρ有界且

显然:Ub⊂U∞⊂U

对任意的ρ∈U∞,记

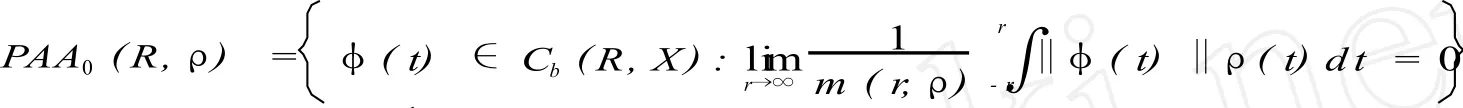
定义 1.6 函数 f∈Cb(R,X)称为加权伪概自守的,如果存在函数 g∈AA(X)及φ∈ PAA0(R,ρ),使得

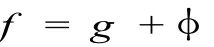
记 R到 X的加权伪概自守函数的集合为W PAA(R,ρ).

定义 1.7 函数 f∈Cb(R×X,X)称为加权伪概自守的,如果存在函数 g∈AA(R×X,X),φ∈PAA0(R ×X,ρ),使得

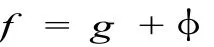
记 R×X到 X的加权伪概自守函数的集合为W PAA(R×X,ρ).

引理 1.8[3]设ρ∈U∞,如果取函数 f∈W PAA(R,ρ)的上确界范数,即

则 (W PAA(R,ρ),‖·‖WPAA(R,ρ))为 Banach空间.

引理 1.9[3]加权伪概自守函数 f=g+φ的分解是唯一的.即如果

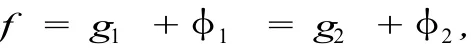
其中 g1,g2∈AA(X),φ1,φ2∈ PAA0(R,ρ),则 g1=g2,φ1=φ2.

引理 1.10[3]设 f∈W PAA(R×X,ρ),若存在常数L ＞0,对一切 x,y∈X和 t∈R,使得 f满足 Lip schitz条件

如果 h∈W PAA(R,ρ),则 f(t,h)∈W PAA(R,ρ)

2.主要结果

假设以下条件成立:

C1f,g是加权伪概自守函数,且存在常数 0＜α ＜1,对任意 x,y∈R,满足 |f(x)-f(y)|≤α|x-y|;

C2函数 hi(i=1,2)是连续的,u(hi)∈W PAA(R,ρ)当且仅当 u∈W PAA(R,ρ);C3函数 Q:(t,x,y)→Q(t,x,y)是加权概自守的且关于 t是连续的,Q =Q1+Q2,其中;

对任意的 v∈W PAA(R,ρ),有 Q2(.,v(.),v(h2(.))∈L1(R),存在 0≤K≤1使得|Q(t,x,y)-Q(t,w,z)|≤k|x-w|+(1-k)|y-z|;

C4t→C(t) ∈ PAA0(R,ρ),C是 L1可积的且

证明:因为 u(t)是加权伪概自守的,由 C2知 u(h2)∈W PAA(R,ρ);

由 C3易知 Q(s,u(s),u(h2(s))也是加权伪概自守的.

设 Q=Q1+Q2,其中 Q1∈AA(R2,R),Q2∈PAA0(R2,R,ρ)

则Γu=Γ1(u)+Γ2(u)

下证Γ1(u)是概自守的.

因为 Q1是概自守的,设 Q1(s,u(s),u(h2)))=h(s),所以,存在函数 g(s)使得

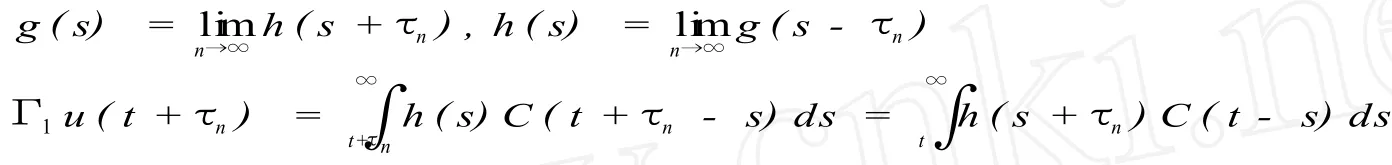
‖h(s+τn)C(t-s)-g(s)C(t-s)‖ =|C(t-s)|‖h(s+τn)-g(s)‖

由 C4知 C(t-s)是有界的,所以存在一M使得上式 ＜M(h(s+τn)-g(s))

当 n→∞时,对任意固定的 s∈R,有 h(t+τn)C(t-s)→g(s)C(t-s)

另外 ‖h(s+τn)C(t-s)‖ ＜M‖h‖

由 L ebesgue控制收敛定理得

同理可证:

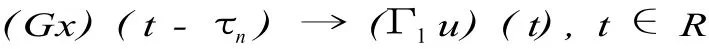
则Γ1u是概自守的.

下证Γ2

因为 t→C(t)∈PAA0(R,ρ),Q2(.,u(.),u(h2(.))∈L1(R)

所以 K=0,既Γ2(u)∈PAA0(R,ρ).

综上所述:函数Γu(t)是加权伪概自守的.

定理 2.2 当α+C0＜1时,积分方程 (1)有唯一的加权为概自守解.

证明:令 u∈W PAA(R,ρ),定义一个非线性算子

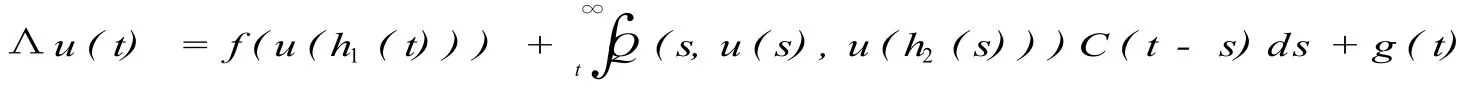
由引理 1.10和 C2易知 f(u(h1(.))∈W PAA(R,ρ),

由定理 3.2知,Λu(t)∈W PAA(R,ρ)

任意取 u,v∈W PAA(R,ρ)

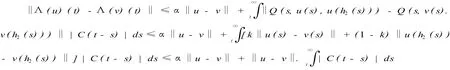
因此 ‖Λ(u)(t)-Λ(v)(t)‖≤ (α +C0)‖u-v‖

当α+C0＜1时,Λ为压缩映射,又W PAA(R,ρ)是完备的,由 B anach不动点定理知,Λ有唯一的不动点 u(t)∈W PAA(R,ρ),使得Λu(t)=u(t).

故方程 (1)有唯一的加权为概自守解.

[1]N’Guérékata G.M.,Almost Automorphic Functions and Almost Periodic Functions in Abstract Spaces[M].Kluwer Academic/Plnum Publisher,New York-Berlin-M oscow,2001.

[2]Diagana T.,Henriquez H.R.,Hern′andez E.M.,Almost automorphic mild solutions to some partial neutral functional-differential equations and Applications[J],Nonlinear Analysis,2008,69:1485-1493.

[3]B lot J,Mophou G.M.,N’Gu′er′ekata G.M.,D.Pennequin,Weighted pseudo almost auto-morphic functions and Applications to abstract differential equations[J].Nonlinear Analysis,2009,71:903–909.

[4]Jing-huai Liu,Xiao-qiu Song,Almost Automorphic and Weighted Pseudo Almost Automorphic solutions of Semilinear E-volution Equations[J].Journal of Functional Analysis,Volume258,2010:196-207.