弧面分度凸轮CAD 技术研究

牟小云

（陕西理工学院机械工程学院，陕西 汉中 723003）

弧面分度凸轮机构（Roller Gear Cam Mechanism）：又称滚子齿式凸轮分度机构，它主要是由装在箱体内的一个空间凸轮和在径向放射状等分地装有滚子的从动盘组成。该机构由输入轴上的弧面凸轮与输出轴分度盘上的滚子无间隙垂直啮合，由凸轮廓面实现分度盘转位和分度盘静止、定位自锁，从而将输入的连续回转运动转化为输出的间歇回转运动。它具有结构简单、刚性好、重量轻、承载能力强、运转平稳、定位准确等特点，可用于高速场合，是目前工作性能最好的间歇转位机构，广泛应用于包装、食品、印刷、烟草、冲压等自动、半自动加工机械，还用于各种机械手、自动生产线。但众所周知，弧面分度凸轮工作轮廓面是空间不可展曲面，很难用常规的机械制图方法绘制，且计算非常复杂，所以在具体绘制时多采用计算机辅助绘图。本文采用编程语言 VC++、逆向工程软件Imerageware、CAD/CAM 集成软件UG 及来共同完成弧面分度凸轮的三维实体模型的绘制。

1 弧面分度凸轮廓面点坐标的计算

1.1 设计计算原理

弧面分度凸轮的设计计算目前一般按照空间包络曲面的共轭原理进行设计计算[1-3]，建立其数学模型。由凸轮和转盘的相对位置和啮合关系建立如图1所示的四套右手坐标系。其中图1(a)为面对2X 箭头看，滚子在距2O 为r 处垂直于X2轴的截面；图1(b)为面对 Z1箭头看，通过凸轮中心1O并垂直于1Z半径为1pr的凸轮截面。

图1 弧面分度凸轮机构的坐标系

各坐标系均用右手直角坐标系，其中：

（1） O0X0Y0Z0——与机架相连的定坐标系；

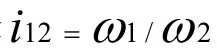
（3） O1X1Y1Z1——与凸轮1 相连的动坐标系；

（4） O2X2Y2Z2——与转盘2 相连的动坐标系。

在图1所示坐标系下可得到公轭接触点K2（K1、K2分别为凸轮与转盘滚子圆柱面的公轭接触点）在坐标系O2X2Y2Z2中的坐标

式中 r 、Ψ —— 滚子圆柱形工作面的方程参数；

Rr—— 滚子半径。

凸轮与滚子的共轭接触方程

式中 φ ——滚子的位置角；

P ——凸轮的旋向系数，左旋为+1，右旋为-1；

C——凸轮与分度盘的中心距。

通过坐标变换得凸轮工作廓面在坐标系O1X1Y1Z1方程如下

式中 φ——滚子位置角

φ = φ0+ pφi

式中0φ ——滚子的起始位置角

iφ ——滚子的角位移，ifSφ φ= ，S 是所选运动规律的量纲，fφ 转盘分度期转位角，iφ 恒取绝对值，0 ≤ φi≤φf。

图中的1L、2L；2R、3R 分别为凸轮分度期工作廓面，L 面为槽左侧脊的右侧，R 面为槽右侧脊的左侧。

1.2 设计计算步骤

在上面公式的基础之上，可得到凸轮廓面点的计算步骤如下：

（1） 按选定的运动规律由每一凸轮转角θ求得转盘相应的角位移iφ 和角速度比（2ω /1ω ），求得棍子的位置角φ。一般取θ ＝1°～2°为一个计算步长。

（2） 选定中心距C 后，把求得的φ 和2ω /1ω 带入共轭接触方程，得到每个θ 滚子圆柱面上共轭接触点的曲面参数r 和ψ 间的制约关系。

（3） 每个θ 时设定一系列的r 值，由上述的制约关系求得相应的ψ ，同一个r 有两个ψ ，ψ ≤90°用于凸轮轮廓R，ψ ≥180°用于凸轮轮廓L。

（4） 把同一θ 时r 和ψ 的每组对应值代入 辊子的坐标方程中，即可求得滚子圆柱面上共轭接触点的坐标X2、Y2、Z2。

（5） 把上述每一θ 时求得的φ 和X2、Y2、 Z2带入凸轮坐标方程式，即得到相应的凸轮工作轮廓的三维坐标值X1、Y1、Z1。

（6） 当凸轮转角θ ＝fθ →360°，转盘停歇，故θ=0 和θ ＝fθ 时的X1、Y1、Z1即为凸轮定位环面的三维坐标值。

1.3 计算实例

本文依据上述步骤，以表1给定条件采用VC++语言编程，来计算单头8工位弧面分度凸轮工作廓面点(分度部分)的坐标。

表1 弧面分度凸轮的给定参数

图2 是计算1L 廓面的程序流程图。

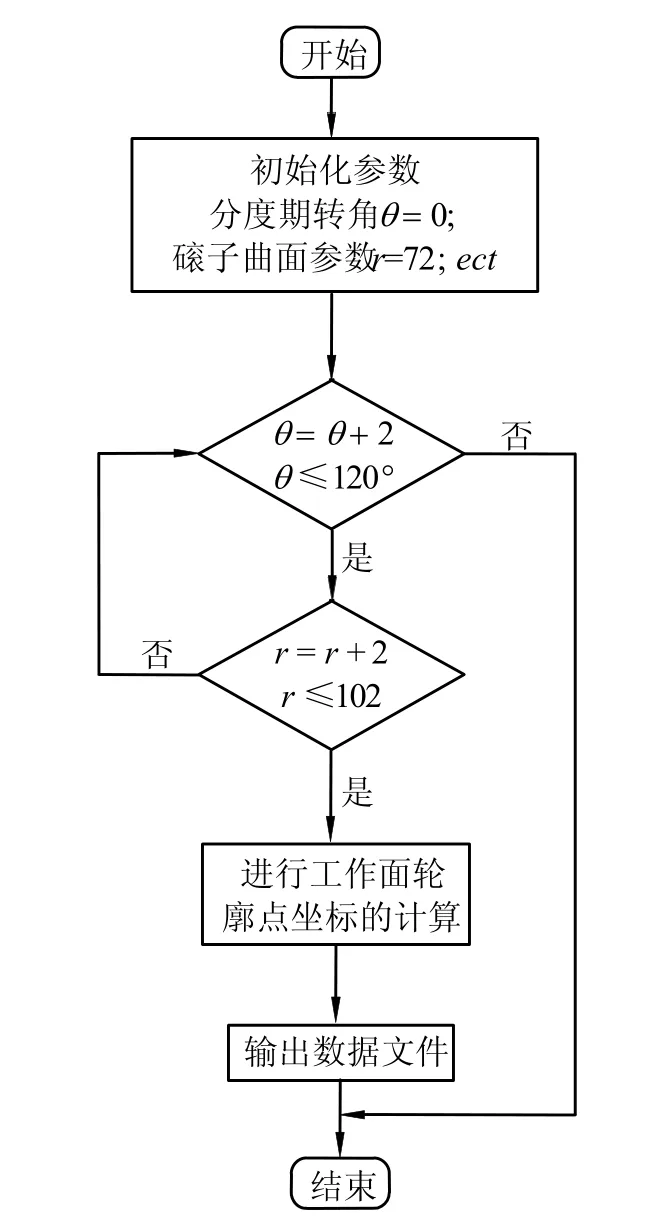
图2 计算廓面点的程序流程图

表2 是曲面1L 廓面的部分三维坐标数据，同理可得曲面2L、2R、3R 的廓面坐标。

2 三维模型的建立

Imageware是美国UGS公司出品的的逆向工程软件，特别适于构造复杂曲面。它可以接受三坐标测量仪器测出的模型表面点阵数据、ASCII、*.dat等多种类型，因此可以将VC计算出的数据保存为文本文件，直接导入Imageware 中，或以*.dat数据直接导入，得到点云如图3所示，然后由点云拟合成曲面。

为了便于后续设计仿真及加工，有必要生成弧面分度凸轮的实体模型。所以在这里选用UG软件，Imageware 是UG 软件中专门为逆向工程设计的模块，两个软件在曲面构造原理上非常类似，通过Imageware 生成的工作曲面，可以直接以*.imw 等文件直接导入UG，如图4 所示，其余曲面可在此基础上采用“扫掠”等命令生成，缝和后自动生成实体，最后求并得到凸轮实体模型如图5(a)所示，图5(b)是弧面分度凸轮机构装配图。

表2 曲面1L 的部分三维坐标数据

图3 Imageware 中的点数据

图4 导入UG 中的曲面

图5 UG 下弧面分度凸轮

3 结 论

这里用VC++计算弧面分度凸轮的点云坐标，然后用Imageware软件生成曲面，最终在UG下生成弧面分度凸轮的实体模型，这样把逆向工程软件和目前流行的三维绘图相结合，减少了不必要的软件开发工作，而且避免了由廓面数据点直接进入UG，而受UG读入行数限制要缝合曲面的过程[4-5]，提高了工作曲面的建模精度（逆向工程软件由点云拟合曲面的精度可达0.01mm）。同时由三维绘图软件构造出弧面分度凸轮及其装配体的三维实体模型，补充了逆向工程软件只能生成曲面模型的不足[6]，为弧面分度凸轮的虚拟设计和虚拟加工提供有效参考，也为后续参数化设计及后续先进加工技术（如：快速原形技术等）奠定基础。

[1] 尹明富, 褚金奎, 吕传毅. 鼓形滚子弧面分度凸轮廓面设计[J]. 机械设计, 2002, 19(2)： 50-52.

[2] 袁恩会, 张 淳, 董继先. 弧面分度凸轮轮廓曲面在计算机上的生成[J]. 西北轻工业学院学报, 2001, 19(1)： 41-43.

[3] 吴文山, 王 莉, 周林航, 等. 基于UG 软件的弧面分度凸轮机构的造型理论与设计[J]. 轻工机械, 2007, 25(4)： 47-50.

[4] 张高峰, 杨世平, 陈华章, 等. 弧面分度凸轮的三维CAD[J]. 机械传动, 2003, 27(6)： 38-40.

[5] 葛文杰, 张王全. 基于Pro/ E 的弧面分度凸轮机构参数化设计与仿真[J]. 机械设计, 2005, 22(1)： 11-14.

[6] 梁延德, 宋丽娟. 弧面分度凸轮的三维建模[J]. 机械设计与制造, 2006, (8)： 142-143.