基于Helmholtz 方程的过渡曲面设计
2010-01-01包崇兵韩旭里
包崇兵, 韩旭里
(中南大学数学科学与计算技术学院,湖南 长沙 410083)
过渡曲面设计在CAD/CAM 中具有重要的地位。其目的是在相关曲面之间生成光滑的过渡曲面,在数学上,过渡曲面的构造可以看作为如 下问题:给定边界为Ω∂ 的有界区域Ω,求解该区域上满足给定边界条件的曲面 ( , )u vX 。典型的边界条件是以X 和它的一些导数在 Ω∂ 上的 值的形式给出,给定导数的阶数取决于过渡曲面与原曲面的连续阶。此外,在某些指定的意义下,对过渡曲面还可能有更进一步的要求,如:光滑、不振荡及与原实体不相交等。
PDE 几何造型方法的思想就起源于将过渡曲面的构造问题看作一个偏微分方程的边值问题[1-7],这种方法简单易行,只要选定原曲面上的过渡线并计算出过渡线处原曲面的跨界导矢,就可用PDE 方法构造出所需要的过渡曲面,实际应用中,通常在三维欧氏空间构造一张曲面 X =X ( x ( u , v ), y ( u , v ), z ( u , v))表示曲面上的点,x = x ( u , v)是参数 u ,v 的函数,参数( u , v )可以视作平面区域Ω 中的点。X 可以视作由Ω 到三维空间 R3中的映射 X : Ω →R3,当 u ,v 分别为常数时的v线,u 线就定义为曲面上的坐标系。 到目前为止PDE 几何造型方法主要针对调和方程和类双调和方程进行研究。
Bloor 等人自20 世纪80 年代将PDE 方法作为一种曲面设计工具引入CAGD 领域以来,对PDE 方法的过渡曲面构造进行了大量的研究,使得该方法可以方便地构造出大量实际问题中的曲面实体。比如:船体、飞机外形、螺旋桨叶片等。国内北京航空航天大学的朱心雄教授等对基于偏微分方程的曲面造型方法开展了研究,并取得了一定的研究成果。然而,到目前为止用偏微分方程进行曲面设计时,人们通常采用如下形式的类调和方程:
二阶偏微分方程

其中 Bloor 等的文献以及国内的一些文献中, 通常将右端项 ( , )f u v 取为零,而仅通过调节形 状参数a 及边界条件来达到调节生成曲面形状的目的。文献[1]、[2]中,讨论了二阶和四阶偏微分方程在过渡曲面设计中的应用进行了研究,分别用解析解和数值解的方法进行了求解,并讨论了形状参数a 对过渡曲面形状的影响。
文献[8]中讨论了Helmholtz 方程的各种解析解的形式及其解的特性,大量文献研究了 Helmholtz 方程的求解及其在机械工程、声学、热能、电磁学等方面的应用。就目前还没有看到有文献将Helmholtz 方程应用于几何造型设计,因此本文给出了如下所示的椭圆型偏微分方程,对其在过渡曲面设计中的应用进行了研究,并讨论了形状控制参数对生成曲面形状的影响。
Helmholtz 方程
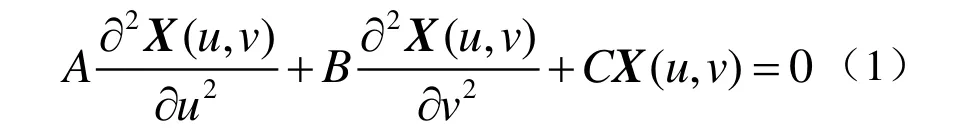
及周期边界条件
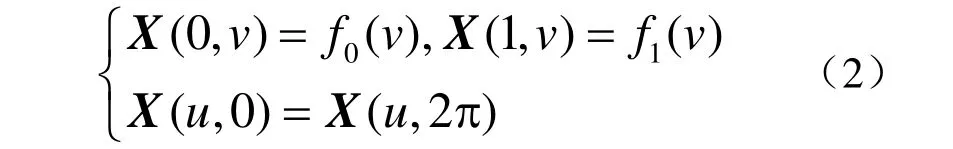
为了得到GC1连续的过渡曲面,将Helmholtz 方程进行如下的扩展,叫做bi-Helmholtz 方程

及周期边界条件
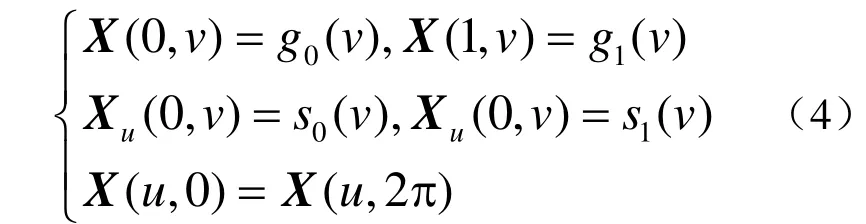
其中 ( , )u vX 为所求曲面,求解区域Ω= {0 ≤ u ≤ 1,0 ≤ v≤ 2 π}, f0( v )和 f1( v)及0( )g v 和1( )g v 为给定的边界曲线,0( )s v 和1( )s v 为对应边界曲线处的跨界导矢,A, B , C , D ,E 为给定的常数。
1 偏微分方程边值问题的差分解法
偏微分方程边值问题有诸多数值解法,如差分法、有限元法、边界元法等,它们有各自的优点和适用范围,而差分方程最为简单、适用面广、易于求解。
对 区 域 Ω= {0 ≤ u ≤ 1,0 ≤ v≤ 2 π}分割:将0 ≤ u≤ 1范围内的u 轴等分为m 段,每段的长度为: Δu = 1/m;同理将v 轴分割成n段,每 段 长 为: Δv = 2 π /n ,离 散 网 格 点( ui, vj), i =0,1, …, m , j =0,1, … ,n ,对方程(3)进行离散化,其中 ( , )u vX 可以是 , ,x y z 中的任何一个分量。采用中心差分近似,以,i jX表示X ( u , v)在( ui, vj)处的值,对 i =2, …, m−2, j = 2, … , n−2。由于

代入式(3)即得差分方程

在区域Ω 上共有( m − 2) × ( n− 2)个内点,因此可以建立( m − 2) × ( n− 2)个方程。但是,当 m ,n 较大时,可以采用迭代方法解决这个问题,迭代法首先把边界条件变形为如下形式
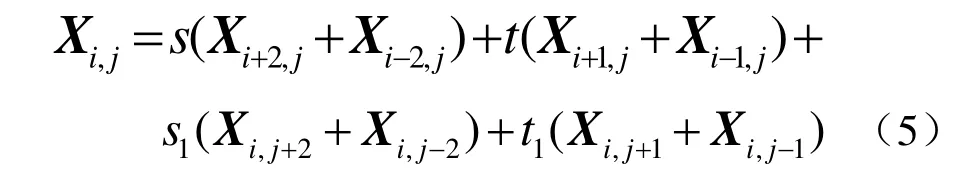
其中

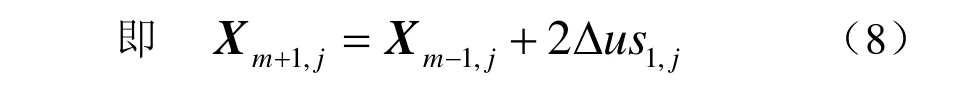
结合边界点,可以得到

迭代算法需要迭代初值的先验知识,采用边界值的平均作初值具有较好的效果,联立(5)~(10)和周期边界条件,可以得到问题的数值解。分别对 , ,x y z 分量求解即可构造出所要曲面。
2 过渡曲面的构造
用偏微分方程边值的方法来构造过渡曲面,其具体步骤如下:
(1) 首先根据过渡曲面与原曲面之间的连续阶来确定合适的偏微分方程。例如:若考虑两 曲面之间进行0GC 拼接,可采用二阶偏微分方 程

若两曲面之间进行 GC1拼接则需要四阶偏微分方程

(2) 确定所需要的过渡曲线,把过渡曲线作为过渡曲面的边界,然后根据偏微分方程的阶数以及原曲面来确定应采用什么样的边界条件以及边界条件值。例如:对二阶偏微分方程,可采用未知函数在边界线上的值作为边界条件;而对于四阶偏微分方程,则采用未知函数在边界线的值和一阶偏导数值作为边界条件。
(3) 通过解析方法或者数值方法求解偏微分方程来生成过渡曲面。
下面用实例来说明如何通过求解偏微分方程来构造所需的过渡曲面。
2.1 构造GC 0 连续的过渡曲面
考虑( , )u v 平面上一个圆与其上方一个球面的 零 阶 过 渡, 假 设 ( u , v )在 区 域Ω = {0 ≤ u ≤ 1,0 ≤ v≤ 2 π}内, ( x , y)平面上的圆以原点为圆心,半径为R;球的半径为 r,球心在 (0,0, z0);取某与平面z = H (0 ≤ H ≤ z0)的交线为过渡线,则其边界条件如下

选择二阶偏微分方程(11),其边界条件由 式(13)给出,当r =2, R=3,04z = , H=3, 通过 数值解的方法得到上述问题的解,由于Helmholtz方程具有很好的光滑性,所得过渡曲面也将具有很好的光滑性。如图1 所示:当参数A 增大时,曲面的形状由上往下向外部膨胀,当参数B 增大的时候,曲面的形状向内部收缩,当参数C 增大时,曲面的形状由下往上向外部膨胀。因此,可以调节参数 , ,A B C 来控制过渡曲面的形状。
由上可知,不同的参数选取,曲面的形状有着明显的变化。在对过渡曲面的拼接处要求不是很高的时候,比如构造上下两个圆之间的过渡曲面时,选择GC0连续有着简洁而计算速度快的优点。当要对两个曲面进行光滑拼接时,就需要构造GC1连续的过渡曲面。

图1 过渡曲面
2.2 构造GC1 连续的过渡曲面
用B样条或Bézier方法构造曲面之间的一阶或二阶过渡曲面,其控制顶点必须满足一定的条件。而用PDE方法构造一阶连续的过渡曲面,则仅需给定过渡曲面在两张原始曲面上的边界及跨界导矢,为了得到GC1连续的过渡曲面,选择四阶的偏微分方程(12),并给出边界条件和跨界导矢,而后求解偏微分方程即可。
2.2.1 圆柱面和平面上一圆的一阶过渡
要求在一个圆柱面和一个圆之间构造一阶连续的过渡曲面,圆所在平面的法矢与圆柱的轴不平行。为简单起见,设圆柱的轴为x 轴,其半径为r。取圆柱面与平面z H= 的截线为过渡线 之一,另一过渡线取球面 x2+ y2+ z2=R2与平面z Cy= 的交线。则可得边界条件和边界切矢 如下

使用方程四阶偏微分方程
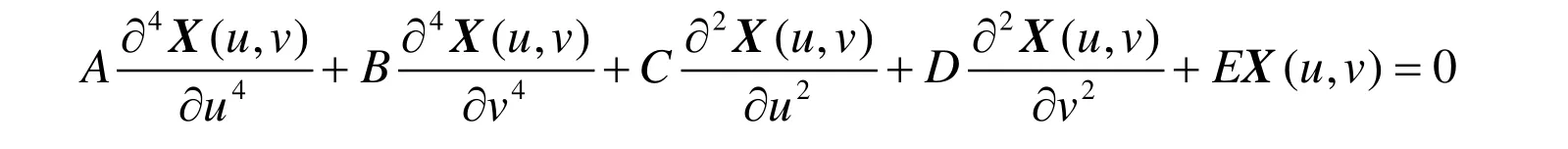
通过数值解的方法可以得到问题的解,当r=2, H=4, R=2, C=2, s=-2 时,所得曲面如图2 所示。
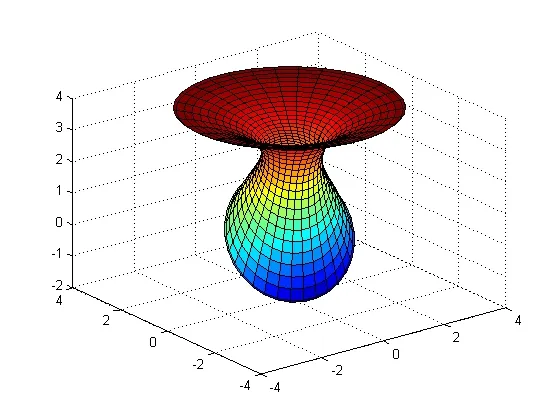
图2 圆柱面斜切面和平面上一圆的GC1 过渡
2.2.2 平面上一圆与其上方一个球面的一阶过渡
在2.1 节中讨论了( , )u v 平面上一个圆与其上 方一个球面的零阶过渡,本节在给出上述边界条件的基础上,再给出跨界切矢

选择四阶的偏微分方程( 12 ), 当r = 2, R = 3, z0= 4, H = 3时,可得一阶过渡曲面如图3 所示。
3 曲面形状控制
通过调整边界条件中的切矢的大小和方向及方程中的系数,可以控制曲面的整体形状,这种控制不是局部控制,因而不影响曲面的整体美观性,不过由于采用了数值解法,边界控制就更加灵活了,在2.1 节中重点讨论了方程中的系数对曲面形状的影响,本节以一个简明的例子对控制方法加以说明。
构造通过圆心分别为(0,0,0)和(0,0,8),平行于xy 平面的两个圆的过渡曲面,经适当参数化后可得边界条件

若 r = R= 0,则所构造曲面即是两个圆之间的过渡曲面,其他情况是构造自由曲面,本例用以 说明边界条件对曲面形状的影响,通过调整,r R 而得到不同形状的带状曲面。如图4 所示。
4 结 论
本文阐述了二阶和四阶Helmholtz 方程的一类周期边界问题的差分解法及其在过渡曲面设 计中的应用,它不同于传统的PDE 方法中的二阶和四阶的偏微分方程,比传统的二阶和四阶偏微分方程有了更多的自由项。因此,在曲面设计的时候,就有更多的形状控制参数可进行调整,文中重点讨论了方程中的系数对曲面形状的影响。当对曲面的拼接要求不是很高的时候,可以用二阶Helmholtz 方程构造GC0连续的过渡曲面,有着形式简洁而计算量小的优点,而当需要对曲面进行光滑拼接的时候,则可以用四阶的bi-Helmholtz 方程构造GC1连续的过渡曲面。并简要说明了边界切矢条件对曲面形状的影响及其在曲面形状设计中的应用,由于采用数值解法,可以构造较为复杂的曲面,曲面设计也较为直观。设计者只需要给出边界曲线和边界切矢并通过控制边界曲线和边界切矢以便构造和修改曲面形状。
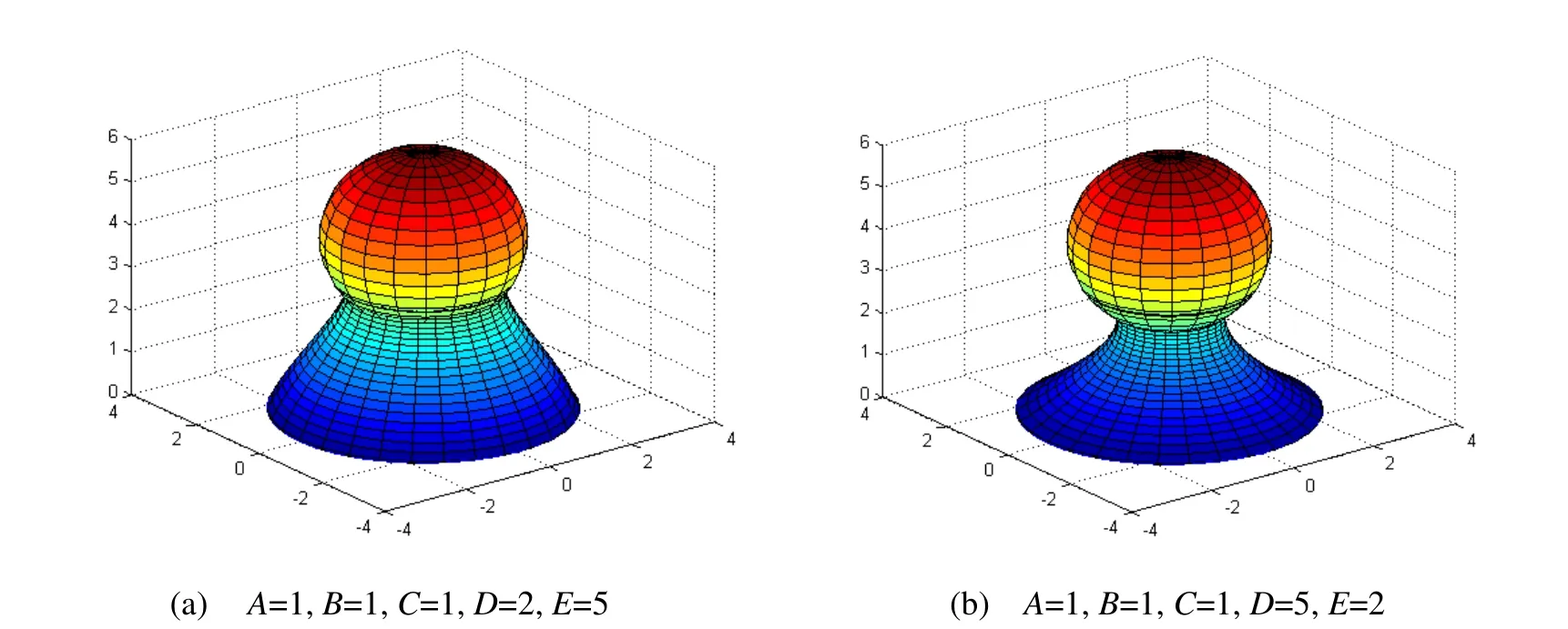
图3 平面上一个圆与其上方一个球面的GC1 过渡
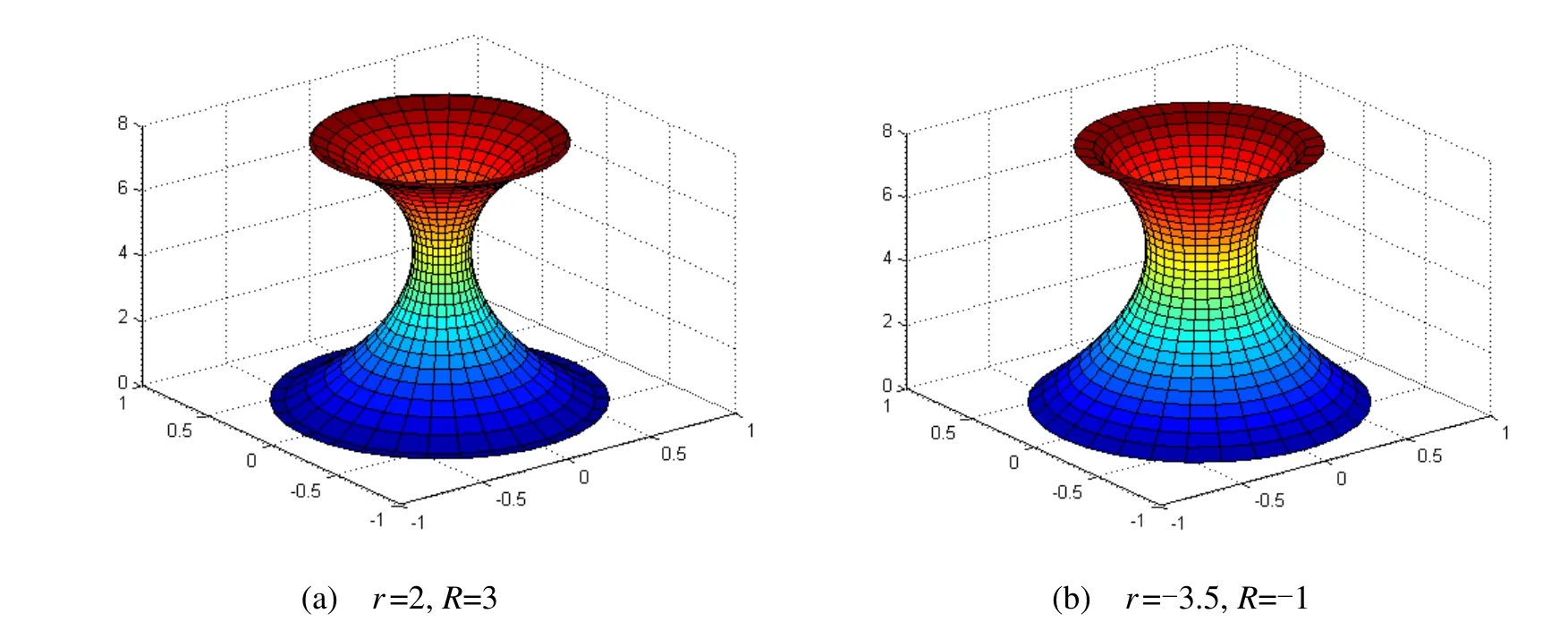
图4 相同边界不同切矢的不同的GC1 过渡曲面
[1] 马 玲, 张 鲜, 朱心雄. 用偏微分方程构造过渡曲面[J]. 工程图学学报, 1995, (1): 1-8.
[2] 马 玲, 张 鲜, 朱心雄. 用偏微分方程数值解构造过渡曲面[J]. 工程图学学报, 1995, (2): 8-14.
[3] 朱心雄, 马 玲. 偏微分方程曲面造型方法及其应用[J]. 航空制造工程, 1997, 176(8): 29-31.
[4] 朱心雄等. 自由曲线曲面造型技术[M]. 北京: 科学出版社, 2000. 256-270.
[5] Bloor M I G, Wilson M J. Generating blend surfaces using partial differential equations [J]. Computer Aided Design, 1989, 21(3): 165-171.
[6] Bloor M I G, Wilson M J. Blend design as a boundary-value problem [C]//Theory and Practice of Geometric Modelling, 1989: 221-234.
[7] Bloor M I G, Wilson M J. Using partial differential equations to generate free-form surfaces [J]. Computer Aided Design, 1990, 22(4): 202-212.
[8] Andrei D Polyanin. Handbook of linear partial differential equations for engineers and scientists [M]. Chapman &Hall/CRC, 2002. 436-456.
