B-样条曲线升阶的几何收敛性

朱 平 ， 汪国昭

（1. 浙江大学数学系计算机图像图形研究所CAD&CG国家重点实验室，浙江 杭州 310027； 2. 东南大学数学系科学计算实验室，江苏 南京 211189）

B-样条具有表示设计自由型曲线曲面的强大功能，是几何形状描述的主流方法之一。升阶是B-样条曲线经常遇到的问题。通过升阶，可以增加B-样条曲线的自由度。同时升阶算法也在B-样条曲线合并、构造张量积曲面有着广泛的应用。尤其在表示和设计组合曲线，B-样条曲线的升阶是必不可少的手段之一。两条或若干条不同次数的B-样条曲线要顺序连续成为一条组合B-样条曲线，用一个统一的方程表示，必须对其升阶，统一其次数。有鉴于此，很多国内外学者都提出了B-样条曲线的快速升阶算法[1-5]。在CAGD 中，许多曲线曲面生成都可以解释为割角的过程，这样的好处是提供了一个很简便的几何构造法[6-7]。但是，除文献[8]外，所有升阶算法都不能解释为几何割角的过程。文献[8]通过提出双次数B-样条解决了这个问题，使得B-样条的升阶有了几何意义，其方法就是不断嵌入节点，生成双次数B-样条曲线。那么通过这种方式升阶，其割角的控制多边形是否像Bézier 曲线[9]那样收敛到原始的B-样条曲线呢？本文通过证明给出了答案。根据本文的结论，B-样条曲线就可以像Bézier 曲线那样割角生成。

1 B-样条曲线的升阶割角

B-样条曲线的定义如下[10]：

其节点向量为

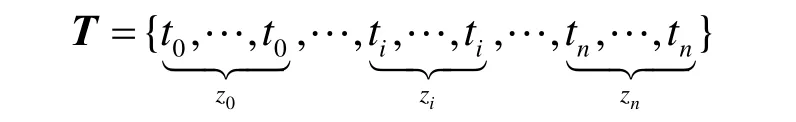
{ Pi}0是控制顶点，{ Ni,k(t )}是定义在T 上k 次 B-样条基函数。

定义在jT 上的双次数B-样条定义如下[8]

这里 lj= z0+ z1+ … + zj+j 。

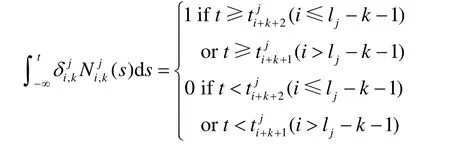
由双次数B-样条的变换公式[8]，很容易将B-样条升阶解释为一个几何割角的过程。下面，通过定理说明通过这样的割角形成的控制多边形序列最终收敛到初始的B-样条曲线。

2 B-样条曲线升阶的收敛性定理

根据文献[8]，将k 次B-样条曲线 ( )tP 升阶至k+ 1次是通过依次嵌入节点定义的双次数B-样条基函数变换实现的。同时，这个变换过程也是对控制多边形割角的过程。下面证明对B-样条初始曲线不断地升阶，其控制多边形最终将收敛到初始B-样条曲线。

为了叙述方便，引入一些记号：

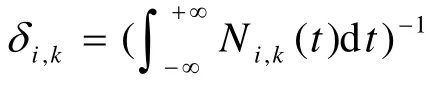
（2） Ni,K( t )是升阶后定义在 T ′上的K 次B-样条基函数。 T ′是升阶后的节点向量

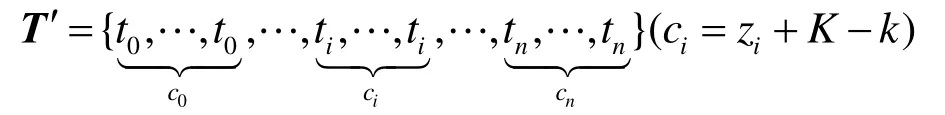
（3） ( ti, ti+1)为节点区间，若 ti＜ ti+1，则 称为非零节点区间。

2.1 基函数的积分估计

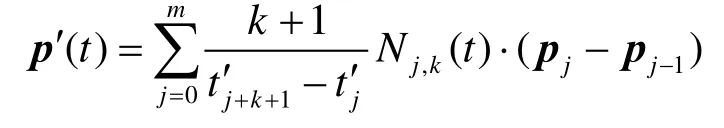
看出 p′ (t )是完全定义在T 上。这样，令Ni,k(t ) = p′ ( t)以及基函数的线性无关性，得到

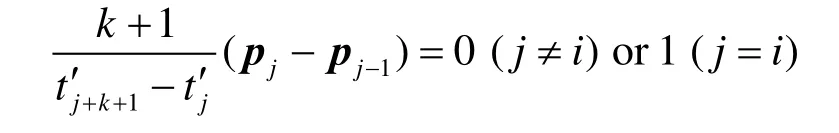
根据 Ni,k( t ) = p ′( t)，知道 p( t ) = 0(t ＜)。则再由基函数的局部性和线性无关性， 得到p−1= …= pi−1=0。那么推得 取t=+∞，可知定理成立。

2.2 控制多边形的收敛性

证明设B-样条曲线

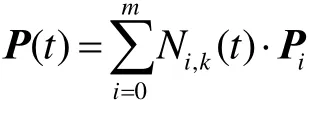
如果对 T ′的每个 ti(i = 0,… , n)分别嵌入一次节点，相当于升阶一次得到新的控制多边形为 Γ3， 容易知道

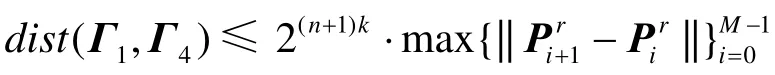
3 图 示

以下为对B 样条控制多边形进行升阶各角得到的B 样条曲线（见图1～图4）。

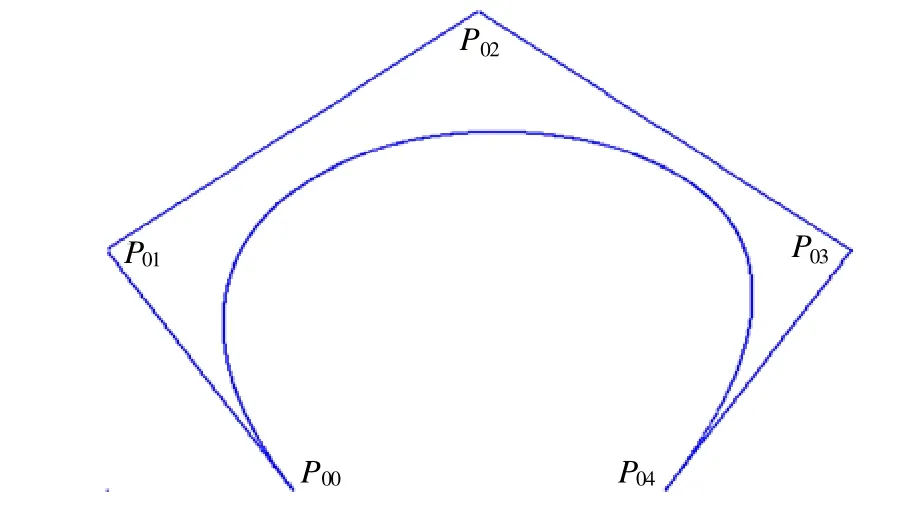
图1 初始控制多边形及B-样条曲线

图2 升阶一次以后的控制多边形

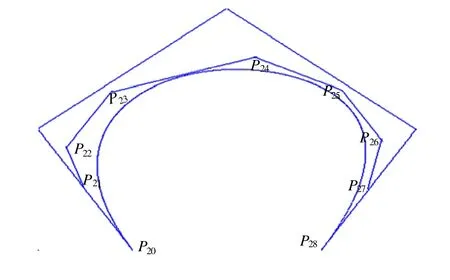
图3 升阶两次以后的控制多边形

图4 升阶五次以后的控制多边形

4 结 论

文献[8]通过插入节点将B-样条曲线的升阶解释为割角的过程，使升阶有了几何意义。本文也可以看成是升阶收敛的又一种证明方法，是对文献[8]的一个补充，通过证明得出了升阶最后逼近收敛的结论，这样就可以像Bézier 曲线那样对控制多边形割角生成B-样条曲线。

[1] HUANG Qixing, HU Shimin, Martin R. Fast degree elevation and knot insertion for B-spline curves [J]. Computer Aided Geometric Design, 2005, 22(2): 183-197.

[2] 孙景楠, 王仁宏. B-样条曲线升阶算法中问题及其解决办法[J]. 大连理工大学学报, 2003, 43(4): 397-398.

[3] 于丕强, 施锡泉. B-样条曲线升阶的新研究[J]. 应用数学, 2003, 16(1): 29-33.

[4] Liu W. A simple, efficient degree raising algorithm for B-spline curve [J]. Computer Aided Geometric Design 1997, 14(7): 693-698.

[5] Prautzsch H, Piper B. A fast algorithm to raising the degree of B-spline curves [J]. Computer Aided Geometric Design, 1991, 8(4): 253-266.

[6] de Boor C. Cutting corners always works [J]. Computer Aided Geometric Design, 1987, 4(2): 125-131.

[7] Paluszny M, Prautzsch H, Schäfer M. A geometric look at corner cutting [J]. Computer Aided Geometric Design, 1997, 14(5): 421-447.

[8] WANG Guozhao, DENG Chongyang. On the degree elevation of B-spline curves and corner cutting [J]. Computer Aided Geometric Design, 2007, 24(2): 90-98.

[9] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M]. 北京: 高教出版社; 海德堡: 施普林格出版社, 2001. 8-9, 28-29.

[10] Piegl L, Tiller W. The NURBS book (2nd ed.)[M]. Berlin: Spring, 1997. 81-82.