逆行地球同步轨道特性探索

刘 赞，高益军

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京 100190）

逆行地球同步轨道特性探索

刘 赞1，2，高益军1

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京 100190）

为了探索逆行地球同步轨道在主要环境力作用下的轨道特性，给出了适合进行数值仿真的轨道动力学模型，并以先进的RKDP方法进行求解.对所得仿真数据利用求和取平均的方法去除摄动力产生的短周期效应，通过分析去短周期项后的数据揭示出了逆行地球同步轨道的演变特点.

逆行地球同步轨道；轨道动力学；RKDP方法；轨道特性

逆行地球同步轨道（RGSO，retrograde geosynchronous orbit）特指轨道周期等于地球自转周期、轨道倾角等于180°的轨道.由于它一天之内可以在地球同步轨道高度绕地球飞行两圈，故可以考虑用它对一系列不同经度位置的重要静止轨道卫星执行一些有价值的任务，这是静止轨道（GEO，geostationary orbit）或类静止轨道卫星所难以胜任的.

然而，国内外很少见到有讨论逆行地球同步轨道的文献，本文旨在对其轨道特性进行初步的探索，希望对相关工作的开展有所启发.

当地球卫星轨道倾角等于180°时，各类常见摄动运动方程均会出现不同程度的奇异性［1-2］.为此，首先给出轨道动力学模型，然后采用先进的数值方法（RKDP法）求解该动力学方程，最终通过对数值仿真解的处理和分析揭示出逆行地球同步轨道的演变特性.

1 轨道动力学模型

地球卫星的轨道动力学模型由轨道动力学方程和环境力模型组成.

轨道动力学方程描述了轨道运动状态与航天器的质心所受的外力之间的动力学关系.轨道运动状态由轨道根数定义，而选择不同的轨道根数，往往方程的具体形式、适用性及方便性也不尽相同.综合适用性和方便性的考虑，本文选用航天器在J2000地心平赤道坐标系下位置和速度矢量的笛卡尔分量作为动力学方程所用轨道根数.这个做法有三个好处：动力学方程形式简单并适用于任意类型航天器轨道；利用现有算法可方便地实现笛卡尔根数与其他各类常见根数之间的转换［2］；日月引力及太阳光压可直接表达在J2000地心平赤道坐标系中，而地球引力在地固坐标系中的分量又可利用现有的算法准确地转换到J2000地心平赤道坐标系下［1］.

1.1 轨道动力学方程

卫星运动一般方程的矢量形式为

式中，r、F0和Fε分别表示卫星的地心距矢量、地球的球形中心引力和各种轨道摄动力的合力.

对于逆行地球同步轨道有摄动力合力

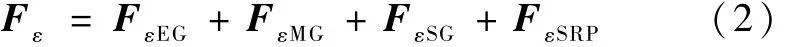
式中，FεEG、FεMG、FεSG和 FεSRP分别表示地球非球形引力摄动、月球引力摄动、太阳引力摄动和太阳光压力摄动产生的摄动力.

在J2000地心平赤道坐标系下，矢量方程（1）可以改写为如下标量形式：

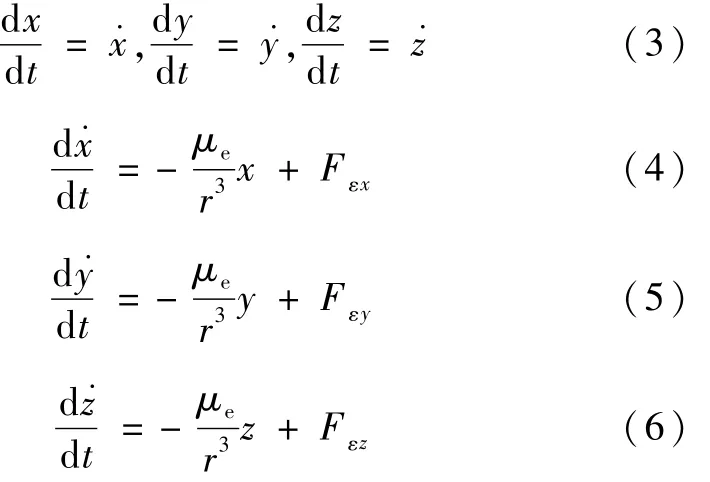
方程（4）～（6）右端第一项和第二项分别对应方程（1）右端第一项和第二项在 J2000地心平赤道坐标系下的分量.r表示地心距，而 x、y和 z是 r在 J2000地心平赤道坐标系下的分量.该方程组适用于对任意类型的轨道进行数值仿真计算.计算所得笛卡尔根数可用文献［2］中4.9节的算法转换成经典轨道根数的形式；相应的，以经典轨道根数给出的初值可用该文献4.8节的算法转换成笛卡尔根数的形式.

1.2 环境力

1.2.1 地球非球形引力

在地固坐标系下，由地球引力模型EGM96所给地球引力势函数可导出地球非球形引力在地心距方向、地心纬度圈切线方向和地心经度圈切线方向产生的摄动力分量为

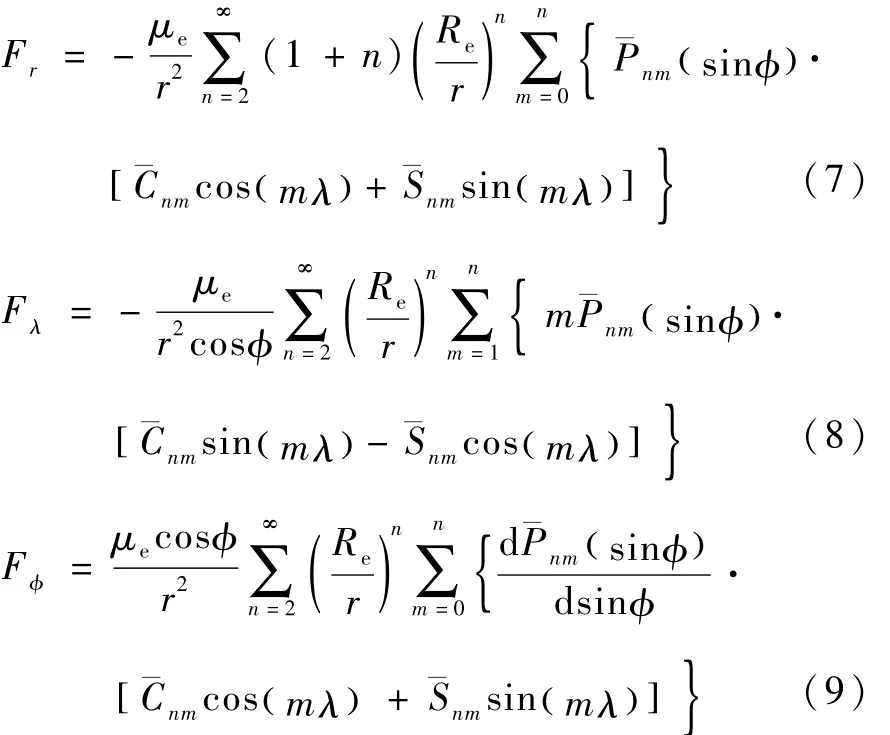
式中，Re表示地球赤道半径，λ和φ分别表示航天器地心经度和地心纬度.μe、和分别为地球引力常数和归一化地球引力系数，其值可参考地球引力模型EMG96（sinφ）为归一化缔合勒让德多项式.ˉPnm（sinφ）及其对sinφ的导数的计算可采用递推算法［1，4］.采用归一化的量和参数是为了提高计算的精度.对地球同步轨道而言，至多只需考虑到12阶12次的地球引力球谐项［5］.

受岁差、章动的影响，航天器在地固坐标系中的坐标（x′，y′，z′）与其在 J2000地心平赤道坐标系中的坐标（x，y，z）之间存在如下关系：

式中（HG）表示从J2000地心平赤道坐标系到地固坐标系的坐标变换矩阵，其具体形式见参考文献［1］的 1.4节.

易得航天器的地心经纬度为

地球非球形引力在地固坐标系下的分量矩阵（Fr，Fλ，Fφ）与 J2000地心平赤道坐标系下的分量矩阵（FεEGx，FεEGy，FεEGz）之间有如下转换关系：

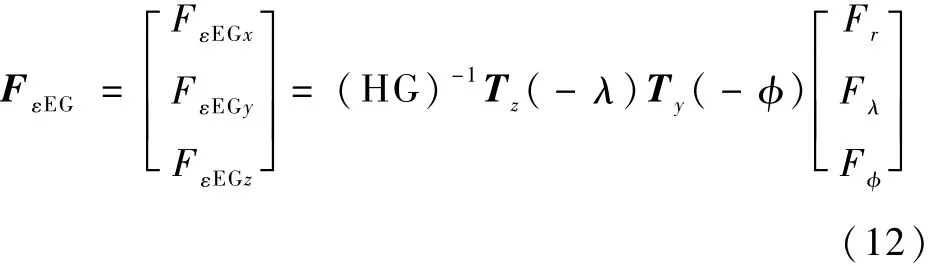
式中（HG）－1是（HG）的逆矩阵，坐标轴旋转矩阵 Tz（－λ）和 Ty（－φ）形式如下：

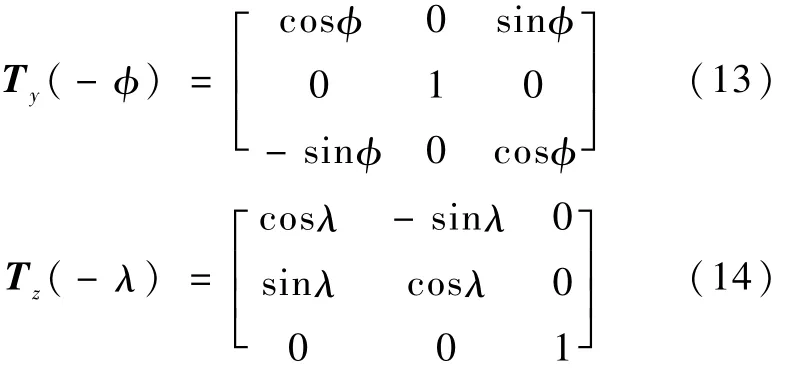
1.2.2 日月引力引起的摄动力

太阳引力产生的摄动力FεSG及月球引力产生的摄动力 FεMG分别为［1］

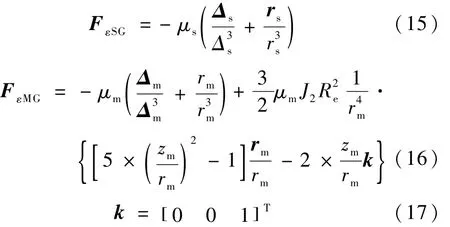
式中，rs和rm分别为太阳和月亮相对地球的位置矢量，rs和rm是它们的模；k为 J2000地心平赤道坐标系Z轴方向的单位矢量，zm则是rm在该方向上的分量；μs和 μm分别为太阳和月球的引力常数.Δm和Δs分别为航天器相对太阳和月球的位置矢量，Δm和Δs是它们的模.太阳位置矢量的计算可参考文献［6］，而高精度月球位置矢量可由DE405星历文件解算得来.由于各位置矢量可直接表达在J2000地心平赤道坐标系下，故不需对 FεSG和 FεMG的分量矩阵做任何变换.

1.2.3 太阳光压产生的摄动力

太阳光压产生的摄动力为［1］

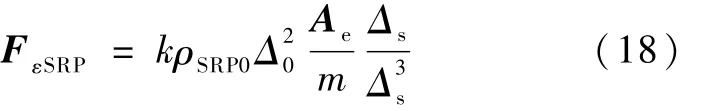
式中，k为与卫星反射率相关的系数，Ae为卫星等效截面积，m为卫星质量，Δ0是日地平均距离，ρSRP0是Δ0处太阳光压强度.该摄动力也可直接表达在J2000地心平赤道坐标系下，无需进行坐标变换.

1.3 求 解

用特殊摄动法求解卫星轨道运动方程比较实用的算法有Gauss Jackson方法（简记为GS法）、RKF7（8）方法［7］、Bulirsch Stoer外推法［8］（简记为 BS法）及 RKDP方法［7-9］.文献［10］显示圆轨道情况下（定步长），GS法速度最快，而 BS法的速度则慢许多，RKDP方法的速度介于两者之间.GS法和BS法的计算精度均能达到10－8，而 RKDP方法则可达到10－6.大椭圆情况下（变步长），RKDP方法速度最快，BS法次之，而GS法则不太适应变步长的积分.此时，RDKP方法的计算精度仍能达到10－6，而 BS法只能达到10－5.

实际上，经过多年的发展，从某些软件的表现来看即便是近圆轨道，变步长的BS法和RKF7（8）方法也要比定步长的GS法快，尤其是变步长的RKF7（8）方法.RKF7（8）方法的优异表现证明了高阶RK方法加入步长控制机制后在计算速度上有很强的竞争力.这印证了前人所做的分析［7］，RK方法阶次越高稳定域越快，而稳定域更宽则意味着可以选取更大的步长.

本文采用先进的八阶 RKDP方法［7，9］，它采用PI控制器进行步长控制［11-12］，既能提高运算速度又能克服刚性问题.此外，它还具有密集输出［7，9］（dense output）能力，可以快速地输出积分轨迹.它最初由Dormand和 Prince在 70年代提出［13］，经过进一步的研究工作［11-12，14-17］才形成现在的八阶算法［7，9］.为了使误差系数最小，Dormand和 Prince对算法中公式的系数进行了优化并采用嵌入式RK公式对进行内部误差估计［14-17］.本文利用该方法对二体轨道进行了长达十年的积分，全局误差的量级为微米级，完全能满足轨道特性分析的要求.

此外，仿真表明，对于RGSO而言，只需考虑到3阶以下地球引力球谐项就可以使轨道预测精度达到10m级.这一结论对于简化近似解析解的求取是非常有帮助的.

2 逆行地球同步轨道仿真分析

通过分析仿真数据，本节给出了逆行地球同步轨道各根数在三种主要摄动力作用下的演变规律，包括长期项和长周期项.长期项指非周期性的变化趋势项，长周期项指周期比轨道周期长的周期性变化趋势项.虽然偏置效应也是一种非周期性趋势项，但由于它不随时间变化，故单独列出.

本节所给各图的数据都经过了去短周期项处理，故反映的是长期项和长周期项效应.

2.1 半长轴的演变规律

地球非球形引力作用下，半长轴有厘米级的周期变化项和米级的负向偏置.月球引力作用下，半长轴有10 m级的周期变化项和百米级的正向偏置，周期项周期等于月球轨道周期.太阳引力作用下，半长轴有米级的周期变化项和百米级的负向偏置，周期项周期为一个季度.太阳光压作用下，半长轴有分米级的周期变化项和10m级的正向偏置.

典型值见图1.

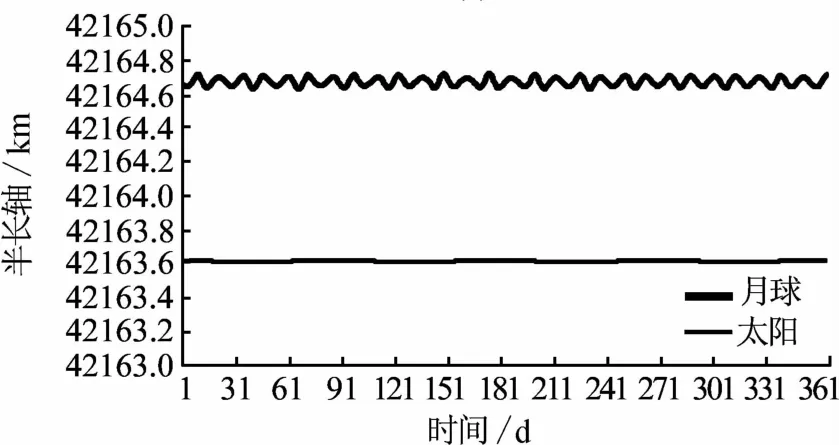
图1 半长轴的演变规律

2.2 偏心率的演变规律

地球非球形引力作用下，偏心率主要有10－5级的偏置.月球引力作用下，偏心率有10－5级的周期变化项，周期等于月球轨道周期.太阳引力作用下，偏心率有10－6级的周期变化项及10－5级的偏置.太阳光压作用下，偏心率有10－4级的周期变化项及正向偏置，周期项周期为一年.日月引力及太阳光压的摄动效应见图2.

2.3 倾角的演变规律

地球非球形引力及太阳光压对倾角的影响几乎为零.月球引力作用下，倾角有10－3级的长期变化项和10－3级的周期变化项.太阳引力作用下，倾角有10－3级的长期变化项和10－2级的周期变化项，周期项周期为半年.

图2 偏心率的演变规律

当地球同步轨道倾角较大时，地球非球形引力对倾角的影响不容忽视.实际上，在它与日月引力的耦合作用下，地球同步轨道倾角变化没有长期变化项，但考虑到RGSO卫星的寿命期有限，尤其从它的定义出发，应该将周期为五十多年的长周期项视为长期变化项.典型值见图3.

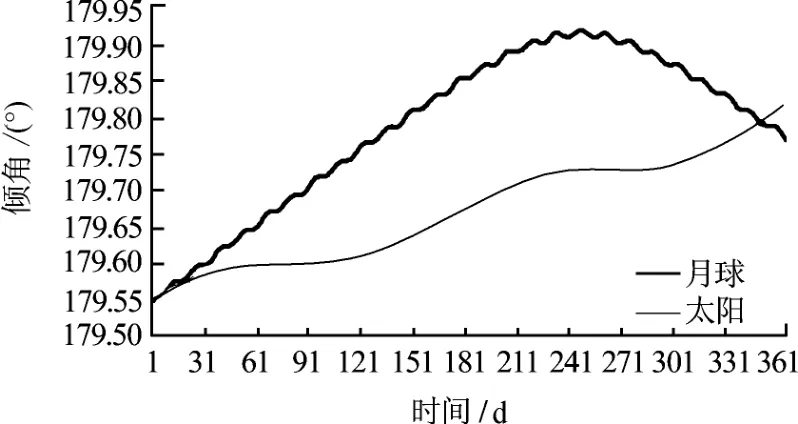
图3 倾角的演变规律

2.4 升交点赤经的演变规律

地球非球形引力作用下，升交点赤经有10－2级的长期变化项.日月引力摄动对升交点赤经的影响与初始条件有关.然而，由升交点赤经和倾角定义的倾角矢量却有着与初始条件“无关”的变化趋势，且只有当轨道节线初始方向与该变化趋势方向一致时才能获得稳定的升交点赤经.太阳光压作用下，升交点赤经有10－5级的周期变化项.

图4（b）中月球相关曲线的大斜率段对应图3中月球相关曲线在180°附近的那段，这时升交点赤经快速变化并由一种平稳状态进入另一种平稳状态.

图4（b）表明，当初值为 270°时，升交点赤经将处于相对稳定的状态.

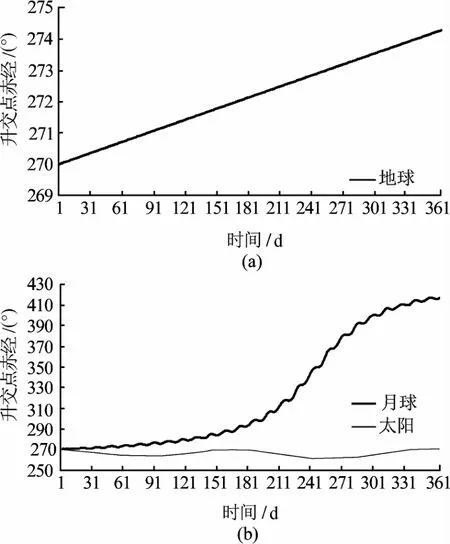
图4 升交点赤经的演变规律

2.5 近地点幅角的演变规律

地球非球形引力作用下，近地点幅角有10－2级的长期变化项.月球引力作用下，近地点幅角有10－2级的长期变化项和100级的周期项，周期项周期等于月球轨道周期.太阳引力作用下，近地点幅角有100级的偏置和100级的周期变化项，周期项周期为半年.太阳光压作用下，近地点幅角有100级的偏置效应和101～102级的周期项，周期项的周期为一年.实际上，各摄动力对近地点幅角的周期项效应均与偏心率的初值有关，偏心率初值越小，周期项变化的幅值越大.

图5（b）中月球相关曲线的大斜率段与图4（b）中对应段相关，因为近地点幅角是从升交点起量的.

3 结 论

不考虑短周期效应，在主要环境力作用下，逆行地球同步轨道的演变过程有如下特点：半长轴受日月引力影响，正向偏置0.3 km后基本保持不变，即轨道周期基本恒定；偏心率受太阳光压影响有一个10－4级的周年变化，受月球引力影响有一个10－5级的周月变化；倾角受日月引力影响以0.85（°）／年的平均速度增加或减小，变化方向与升交点赤经初值有关且当倾角等于180°时改变变化方向；升交点赤经主要受日月引力影响，同时在地球非球形引力作用下缓慢东进；近地点幅角受太阳光压影响做周年变化，其幅值与偏心率初值有关，而变化区间所在象限则与偏心率矢量的初值有关.

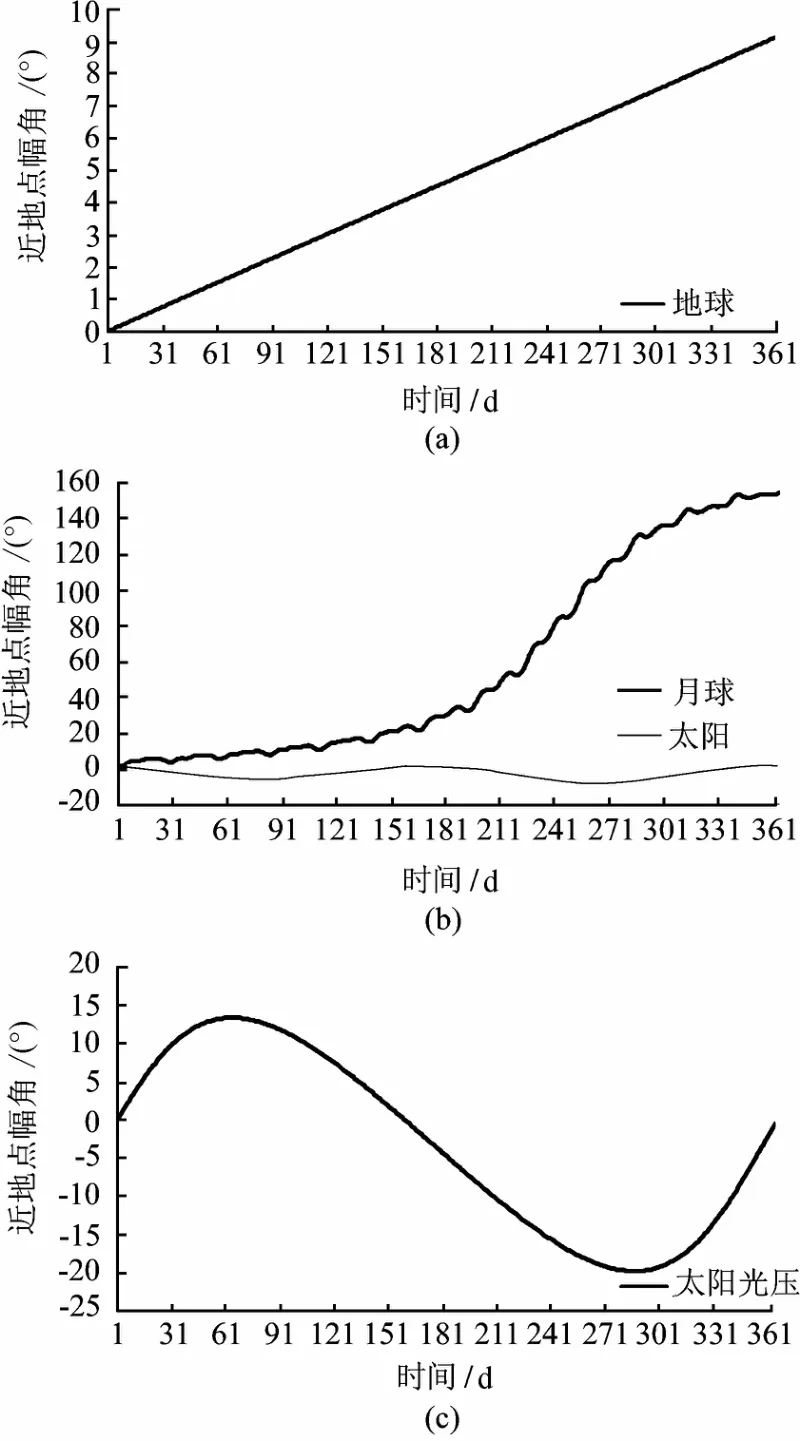
图5 近地点幅角的演变规律

［1］刘林.航天器轨道理论［M］.北京：国防工业出版社，2000

［2］Vladimir A C.Oribtal mechanics［M］.3rd ed.Reston：American Institute of Aeronautics and Astronautics Inc.，2002

［3］章仁为.静止卫星的轨道和姿态控制［M］.北京：科学出版社，1987

［4］张强，刘林.关于勒让德多项式的算法问题［J］.紫金山天文台台刊，1996，15（4）：259-283

［5］David A V.An analysis of state vector propagation using differing flight dynamics programs［C］.The AAS／AIAA Space Flight Mechanics，Copper Mountain，Colorado，USA，Jan 2005

［6］郗晓宁，王威.近地航天器轨道基础［M］.长沙：国防科技大学出版社，2003

［7］Hairer E，Norsett S P，Wanner G.Solving ordinary differential equations I：non－stiff problems［M］.2nd ed.New York：Springer，1993

［8］Stoer J，Bulirsch R.Introduction to numerical analysis［M］.3rd ed.New York：Springer，2002

［9］Willam H P，Saul A T，William T V，Brian P F.Numerical recipes：the art of scientific computing edition［M］.3rd ed.New York：Cambridge University Press，2007

［10］Ken F.Numerical integration of the equations of motion of celestial mechanics［J］.Celestial Mechanics and Dynamical Astronomy，1984，33（2）：127-142

［11］Gustafsson K.Control theoretic techniques for stepsize selection in explicit Runge-Kutta methods［J］.ACM Transactions on Mathematical Software，1991，17（4）：533-554

［12］Soderlind G.Digital filters in adaptive time-stepping［J］.ACM Transactions on Mathematical Software，2003，29（1）：1-26

［13］Dormand J R，Prince P J.New Runge-Kutta-Nystrom algorithms for simulation in dynamical astronomy［J］.Celestial Mechanics and Dynamical Astronomy，1978，18（3）：223-232

［14］Dormand JR，Prince P J.A family of embedded Runge-Kutta formulae［J］.Journal of Computational and Applied Mathematics，1980，6（1）：19-26

［15］Dormand J R，Prince P J.Runge-Kutta triples［J］.Computers＆ Mathematics with Applications，1986，12A（9）：1007-1017

［16］Dormand J R，Prince P J.Runge-Kutta-Nystrom triples［J］.Computers＆ Mathematics with Applications，1987，13（12）：937-949

［17］Dormand J R，Prince P J.Practical Runge-Kutta processes［J］.SIAM Journal on Scientific and Statistical Computing，1989，10（5）：977-989

Study of Characteristics of Retrograde Geosynchronous Orbit

LIU Zan1，2，GAO Yijun1
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

To study evolving characteristics of a retrograde geosynchronous orbit influenced by major environmental forces，an orbit dynamics model suitable for numerical simulations is given and solved by the advanced RKDP method.Numerical solutions are periodically summed and averaged to get rid of shortperiodic-term effects.By analyzing polished data，its orbit characteristics are revealed to us.

retrograde geosynchronous orbit； orbital dynamics；RKDP method；orbit characteristics

V448

A

1674-1579（2009）04-0052-05

2008-11-04

刘 赞（1983—），男，湖南人，硕士研究生，研究方向为轨道动力学与控制（e-mail：liuzan＠yahoo.cn）.