深空探测转移轨道自主中途修正方法研究*

2009-12-12张晓文王大轶黄翔宇

空间控制技术与应用 2009年4期

关键词：制导修正探测器

张晓文，王大轶，黄翔宇

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

深空探测转移轨道自主中途修正方法研究*

张晓文1，2，王大轶1，2，黄翔宇1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

针对深空转移轨道，提出以B平面参数为终端参数，采用脉冲控制和线性制导的自主中途修正方法.由自主导航系统定期确定探测器的当前位置和速度，之后利用精确动力学积分递推状态至B平面，得到打靶误差，若误差超出目标精度范围又在自主修正系统修正能力范围内，则立即利用以B平面参数为终端参数的线性制导公式并结合牛顿迭代计算出修正轨道的速度增量.利用中心差分公式计算终端参数对控制参数的敏感矩阵.蒙特卡罗仿真表明，在小偏差前提下该方法能够达到制导目标.

中途修正；B平面；转移轨道；深空探测

自主中途轨道修正是深空探测器实现自主控制的关键技术之一.深空探测器进入转移轨道后，由于存在入轨误差、导航误差和机动执行误差等因素影响不可避免偏离设计轨道，因此需要对其进行中途修正.自主中途轨道修正是指深空探测器在无地面干预情况下利用导航信息自行计算修正轨道所需控制量，然后由推进系统执行的过程.

目前对于中途轨道修正的研究和应用大多基于地面测控方式［1-4］，而对自主执行方式极少涉及.基于地面测控的中途修正事先经过大量的数学计算和仿真分析，精心设计修正方案后上传至探测器执行相应机动.由于星上存储和计算资源有限，显然不能将基于地面测控的中途修正方式直接移植用于自主中途修正，因此有必要研究专门的简化算法.1998年发射升空的“深空一号”探测器首次尝试了基于小推力连续式的自主中途修正技术［5］，为这一领域的研究提供了有益参考.

本文深入研究了转移轨道段的自主轨道修正问题，提出了以B平面参数为终端参数基于速度脉冲控制的自主中途修正方法.

1 中途修正问题

深空探测中途修正并不是把轨道修正为标称轨道，因为从燃料消耗角度考虑这样做不合算.中途修正是在有误差的位置上施加一个合适的速度增量，使探测器沿着一条新的转移轨道飞行来满足对最终状态的要求［5］.

中途修正时刻探测器的初始参数记为P，一般为位置和速度.探测器最终飞抵目标区域的终端参数记为Q.则深空转移轨道终端状态与初始状态的关系可表示为函数

中途修正问题就是利用一定的制导方法使探测器到达目标区域的实际状态Q与期望状态Qnom之间的误差ΔQ小于设定阈值

深空飞行轨道的终端参数常见形式是目标轨道的倾角和近心距，或是B平面参数.

2 B平面参数

Kizner［6］发现建立在目标天体B平面上的参数与探测器飞行轨道状态参数之间存在很好的线性关系.大量的理论分析和工程实践表明，深空探测器的飞行轨道可以用B平面参数来描述目标散布，并且用迭代方法修正B平面参数的误差具有很好的收敛性，较之轨道倾角和近心距等直观目标参数更容易计算得到速度增量［7］.

B平面一般定义为过目标天体中心并垂直于接近目标天体的双曲线渐近线的平面.记进入轨道的渐近线方向的单位矢量为.若目标天体引力影响可以忽略，渐近线方向矢量可以取为探测器的相对速度方向.

B矢量定义为由B平面原点指向轨道与B平面交点的矢量，记为.B平面参数定义为在轴的分量 BT和在轴的分量 BR，则 BT和 BR为

此外，探测器沿飞行轨道到B平面的距离通常用等价的到达时间tTOF来描述.

3 中途修正的线性制导方法

将实际轨道在标称轨道附近泰勒展开保留线性项，得到如下线性控制方程：

式中：K为终端状态对控制参数的敏感矩阵，有K＝∂Q／∂P T；ΔP为控制量.

解控制方程（5）的方法取决于控制量的维数m和终端参数的维数n.采用不同方法求解得到如下3种结果［5］.

（1）n＝m

此时方程组中方程的数量与控制参数的数量相同，最容易求解.只需对敏感矩阵K简单的求逆便可得到控制方程的唯一解ΔP，即

（2）n＞m

此时控制参数的数量少于方程组中方程的数量，利用最小二乘方法求解控制量ΔP.使下面性能指标取得最小值的ΔP便是所求解：

使J最小的控制方程的最小二乘解为

此最小二乘收敛解只能保证性能指标J和残余误差ΔQ最小，不能保证ΔQ一定小于阈值et.

（3）n＜m

此时控制参数的数量多于终端状态维数.在ΔQ＝KΔP的约束下，选幅值最小的修正量ΔP为控制方程的解.性能指标如下：

式中，λ是拉格朗日乘子.利用变分法求得此方程的解为

4 基于B平面参数的中途修正方法

B平面参数的误差定义如下：

以B平面参数作为终端参数，只考虑BR和BT的误差ΔB R和ΔB T时，残余误差为

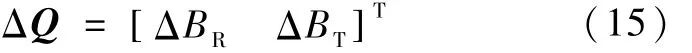
所需速度增量计算公式如下：

用这个修正量来修正初始状态，然后再重新计算残余误差、敏感矩阵和速度增量.这样反复迭代到末端状态满足一定的精度.用迭代后状态减去迭代前状态就是实际要执行的速度增量.此过程属于牛顿迭代算法.

若限定到达时间tTOF，则残余误差为

所需速度增量计算公式如下：

实际要执行的速度增量同样通过迭代求解.式（18）中敏感矩阵的表达式如下：

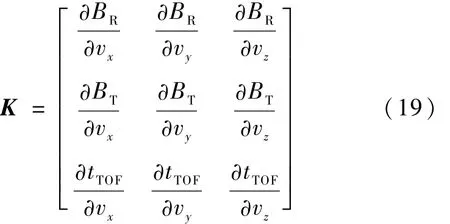
计算敏感矩阵K主要有利用数值差分的方法和利用状态转移矩阵的方法.首先介绍数值差分方法，以计算敏感矩阵第1个元素为例，给出中心差分公式如下［5］：

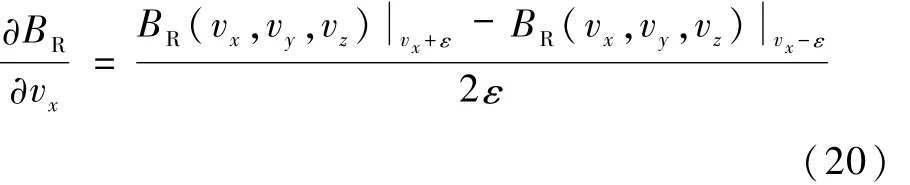
式中，ε是小幅值摄动量，即速度增量，也是差分运算的步长.摄动量ε的取值是利用数值差分方法计算敏感矩阵的关键.

下面介绍利用状态转移矩阵计算敏感矩阵的方法.设状态变量为X＝[r ]vT，其中r和v是探测器的位置和速度，式（5）可以化为

即

式中：X i是探测器在初始时刻的状态；X f是探测器在终端时刻的状态；Φf为终端轨道状态相对初始状态的状态转移矩阵.在式（22）中除Φf外，其余两个偏导矩阵具有确定的表达式.而Φf则需要通过对矩阵微分方程和轨道动力学方程进行数值积分才能计算出来.

首先分析不限定到达时间tTOF的情况.B平面参数Q＝[ BRBT]T与转移轨道终端状态 Xf的解析表达式如下：

则

修正时刻状态对控制变量的导数为

其次分析限定到达时间tTOF的情况.由式（14）可知

到达时间误差ΔtTOF是在标称值附近的小偏差量，因此可以利用二体问题的公式近似表示.中心天体取为在交会时刻对探测器作用力最大的天体.已知t时刻探测器的位置和速度，则由活力公式求出半长轴a为

式中：μ是中心天体的引力常数；r＝‖r‖；v＝‖v‖.偏心率e和t时刻的偏近点角E的计算公式如下：

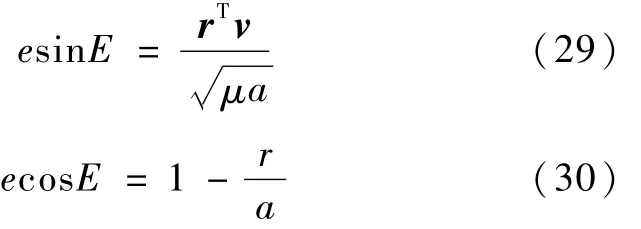
由开普勒方程可得

式中，τ是过近心点时刻.已知轨道上两点的状态（r0，v0）和（r1，v1）就可由上述公式求出转移时间

由式（27）～（32）可以建立终端状态和到达时间的解析关系，继而求得到达时间对终端状态的导数

最后，B平面参数Q＝[ BRBTtTOF]T与转移轨道终端状态Xf的解析表达式如下：

5 自主中途修正方法

在前面研究的基础上，提出以B平面参数为终端参数的深空转移轨道自主中途修正方法，其步骤如下.

1）计算B平面误差.深空探测器进入转移轨道后，利用自主导航系统的周期性确定当前位置和速度，并传递给自主制导系统，利用龙格-库塔算法对动力学模型精确积分来获得最终状态，计算出交会时B平面误差ΔQ.

2）判断是否执行修正.若B平面误差小于下限阈值，即在当前制导精度下轨道偏差在可接受范围内，则不启动本次修正；若B平面误差大于上限阈值，即轨道偏差已经超出自主制导系统修正范围，则立即向地面控制中心下传求助信号；若B平面误差处于上下限阈值之间，则执行下一步.

3）计算修正量.首先由式（20）所示的中心差分公式计算终端状态变量对控制参数的敏感矩阵K，之后利用式（16）或式（18）计算修正量，用龙格-库塔算法和精确的动力学模型对修正后的轨道进行数值积分，再次求出ΔQ和K.这样反复迭代到末端状态满足一定的精度.用迭代后状态减去迭代前状态就是实际要执行的速度增量Δv.

4）执行修正机动.姿态控制系统调整探测器姿态使发动机指向需要方向，接着发动机点火产生指定大小的速度增量，最后探测器恢复正常姿态运行其他任务，等待下一个轨道修正周期的到来.

6 数学仿真

以“凤凰号”火星探测器转移轨道为例进行中途轨道修正的蒙特卡罗仿真.相关轨道数据从NASA网站获得.动力学模型以太阳为中心天体，摄动项考虑8大行星引力及太阳光压.数值积分采用4阶／5阶龙格-库塔算法.轨道起止时间为2007年9月1日～2008年4月26日.

6.1 敏感矩阵分析

1）用数值差分方法计算敏感矩阵.首先分析敏感矩阵中偏导与摄动量的关系，结果见图1.摄动量的变化范围为 10－6～102m／s.

图1给出了B平面参数对初始速度的偏导数随着摄动增大的变化曲线，从中可以看出曲线大致可分为3个区域：噪声区、稳定区和变化区.以BR对初始速度的偏导数为例，当摄动量小于10－5m／s时，曲线形似噪声，故称此区间为噪声区；当摄动量大于100m／s时，偏导随着摄动量增加而大幅变化，故称此区间为变化区；当摄动量大于10－5m／s小于100m／s时，曲线幅值非常稳定，故称此区间为稳定区.实际计算敏感矩阵中的偏导时显然ε应该取在稳定区的中间位置.

图1 B平面参数对初始速度的偏导与摄动的关系

其次分析敏感矩阵中各项偏导数随着制导时间接近终端时刻的变化情况，结果见图2.

图2 B平面参数对初始速度的偏导与制导时间的关系（数值差分方法）

图2 给出了随着制导时间接近终端时刻B平面参数对初始速度的偏导数的变化曲线.从图中可以看出曲线的幅值随着修正时刻逐渐接近终端时刻而减小并趋于0.这与直观分析结果一致，因为探测器已经与B平面相交，所以无论在交点处速度如何变化都不可能改变3个目标参数的数值.

2）用状态转移矩阵方法计算敏感矩阵.分析敏感矩阵中偏导与制导时间的关系，结果见图3.

图3给出了随着制导时间接近终端时刻B平面参数对初始速度的偏导数的变化曲线.从图中可以看出曲线总体而言幅值随着修正时刻逐渐接近终端时刻而减小，但是tTOF对初始速度的偏导数没有收敛于0.这与直观分析结果不一致，也就是说此时敏感矩阵有较大误差.

经过比较，利用数值差分方法和利用状态转移矩阵计算得到敏感矩阵在数值上存在一定差异.

图3 B平面参数对初始速度的偏导与制导时间的关系（状态转移矩阵方法）

6.2 中途修正分析

1）无制导时的 B平面打靶误差.表1给出了在3种情况下的B平面打靶误差.初始时刻位置各分量随机误差为289 km（1σ），速度各分量随机误差为 0.577 m／s（1σ），仿真中随机抽样 400次.从表1中可以看出引起打靶误差的主要因素是初始速度误差.

2）单脉冲中途修正.设初始时刻位置各分量随机误差为 289 km（1σ），速度各分量随机误差为0.577 m／s（1σ）；制导目标取为 B平面靶点距离误差小于10 km，到达时间误差小于60 s；轨道修正执行时间为交会前238 d.制导方法采用以下3种：①利用状态转移矩阵方法计算敏感矩阵且不限到达时间；②利用数值差分方法计算敏感矩阵且不限到达时间；③利用数值差分方法计算敏感矩阵且限定到达时间.表2给出了随机抽样100次的统计结果，其中 ΔBR、ΔBT和 ΔtTOF给出的是 1σ值，Δv和迭代次数给出的是平均值.

表1 无制导时B平面的打靶误差

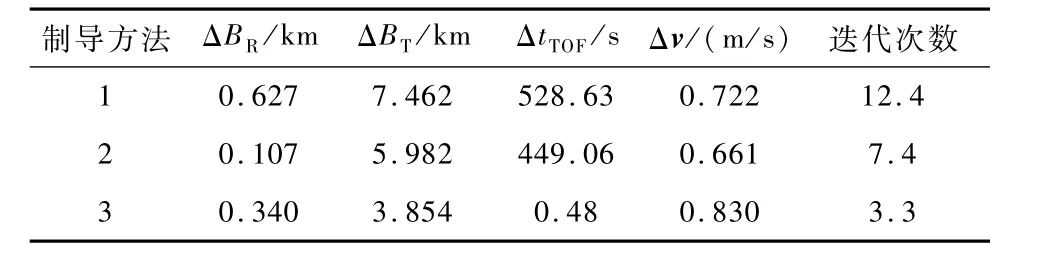
表2 单脉冲中途修正的仿真结果

从表2中可以看出，这3种制导方法均有效，能满足制导目标，且第3种制导方法的修正效果最好，迭代次数最少，但代价是所需的速度增量比其他两种方法大.总体来看，利用数值差分方法计算敏感矩阵的制导方法，无论制导效果、所需速度增量大小和迭代次数都优于利用状态转移矩阵方法计算敏感矩阵的制导方法.

在本算例中，利用状态转移矩阵方法计算得到敏感矩阵的精度较低，可能的原因有以下3种：①由于动力学模型的非线性导致状态转移矩阵存在较大线性化误差；②敏感矩阵对应的摄动量不同，状态转移矩阵方法计算得到的是无穷小速度增量对应的敏感矩阵，而数值差分方法计算得到的是接近实际值的速度增量对应的敏感矩阵；③tTOF的近似表达式存在误差.

3）考虑执行误差的中途修正.实际中推进系统不可避免存在执行误差，下面对这种情况进行仿真.推进执行误差先后取为3%和5%；自主中途修正周期取为7 d；制导目标同前；利用数值差分计算敏感矩阵且限定到达时间；初始误差为x轴方向500 km的位置误差和1 m／s的速度误差.表3给出了仿真结果.

从表3中可知，两种执行误差情况下，修正次数都为3次.后面修正的脉冲都小于其前次修正至少一个数量级.执行误差越大所需总的速度增量也越大.3%执行误差引起的速度增量增幅为6.5%；5%执行误差引起的速度增量增幅为11.1%.

表3 有执行误差时的中途修正结果

4）考虑导航误差的中途修正.实际中导航系统给出的探测器位置和速度信息与真实值存在差异，下面对这种情况进行仿真.导航误差取为x轴方向0.3 m／s；自主中途修正周期取为7 d；制导目标同前；初始误差为 x轴方向500 km的位置误差和1 m／s的速度误差.图4和表4给出了仿真结果.

图4 有导航误差时中途修正所需的速度增量

表4 有导航误差时中途修正结果

由图4可知，有0.3 m／s的导航误差时，每个周期都需要进行修正.其中，第1个脉冲主要用于消除入轨误差，量级最大，达到1.4 m／s.后续的速度增量用于消除导航误差，不过数量级很小，绝大多数小于0.2 m／s，在临近交会时幅值有所上升.总的速度增量相比无导航误差情况增大了145%.最终的B平面误差没有达到制导目标.

将最后一次修正时刻的导航误差减小为0.01 m／s，其余时刻的导航误差仍然为 0.3 m／s，再进行上述仿真，结果残余误差达到了制导目标，见表4.这个仿真结果的启示是：在转移轨道阶段当导航误差较大时，目标参数误差阈值不必取得太小，否则需要频繁施加速度增量进行修正，造成大量燃料浪费；在交会阶段随着相对测量信息的获得，导航精度有了显著提高，此时再减小目标参数误差阈值能实现高精度制导.

7 结论

本文研究了深空探测转移轨道段的自主中途修正问题，提出了以B平面参数为终端参数采用脉冲控制并结合线性制导的自主中途修正方法，其算法相对简单能够在星上实现.蒙特卡罗仿真结果表明，在实际飞行轨道与标称轨道存在小偏差的前提下，不考虑执行误差和导航误差时，利用该方法只需进行一次修正即可使探测器的终端状态达到制导目标；考虑执行误差和导航误差后，利用该方法仍然能够达到制导目标，只是修正次数和总速度增量明显增加，尤其是导航误差对制导性能影响显著；在每个修正时刻，制导目标阈值应根据执行误差和导航误差来设定，如果阈值设定太低，则既无法达到制导目标又需要频繁施加修正脉冲造成的大量燃料浪费.

［1］Raofi B，Bhat R S，Helfrich C.Propulsive maneuver design for the 2007 Mars Phoenix Lander mission［C］.AIAA／AAS Astrodynamics Specialist Conference and Exhibit，Honolulu，Hawaii，August 18-21，2008

［2］Hintz G R， Chadwick C.Design and analysis techniques for trajectory correction maneuvers［C］.AIAA／AAS Astrodynamics Conference， Seattle，Washington，August 20-22，1984

［3］周文艳，杨维廉.月球探测器转移轨道的中途修正［J］.宇航学报，2004，25（1）：89－92

［4］杨嘉樨，吕振铎，孙承启，等.航天器轨道动力学与控制［M］.北京：宇航出版社，2002

［5］Desai S D，Bhaskaran S，Bollman W E，et al.The DS-1 autonomous navigation system：autonomous control of low thrust propulsion system ［C］.AIAA Guidance，Navigation and Control Conference， New Orleans，USA，August 1997

［6］Kizner W.A method of describing miss distances for lunar and interplanetary trajectories［J］.Planetary and Space Science，1961，7：125-131

［7］谷立祥，刘竹生.使用遗传算法和B平面参数进行月球探测器地月转移轨道设计［J］.导航与航天运载技术，2003（3）：1-5

Study on the Autonomous Midcourse Correction during Cruise Phase of Interplanetary Exploration

ZHANG Xiaowen1，2，WANG Dayi1，2，HUANG Xiangyu1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

Autonomous midcourse correction is a key technique to facilitate autonomy of an interplanetary spacecraft.Using B-plane parameters as target parameters and impulse control method combined with linear guidance，an autonomous orbit correction method used during cruise phase of interplanetary orbit is proposed.First，the navigation system periodically determines positions and velocities of the spacecraft.The states are then mapped onto the B-plane by integrating the dynamics model accurately.If deviation from the desired encounter condition is large enough and is not out of the capability of autonomous midcourse correction system，the velocity increment for correction maneuver is computed by using linear guidance formula combined with Newton iteration method.The sensitivity matrix of target parameters relative to control parameters is numerically computed using finite central difference formula.Monte Carlo Simulation shows that this method is capable of guiding the spacecraft to a successful encounter.

midcourse correction；B-plane；transfer orbit；deep space exploration

V448.2

1674-1579（2009）04-0027-07