绕飞慢旋目标参数自适应积分滑模控制*

刘智勇，何英姿

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

式中，

绕飞慢旋目标参数自适应积分滑模控制*

刘智勇1，2，何英姿1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

针对满足一定条件的一类不确定部分上界不确知的系统，提出了一种参数自适应积分滑模控制策略.通过在切换函数中引入跟踪误差积分项，消除了传统滑模变结构控制需要被跟踪信号导数已知的假设.同时基于Lyapunov方法引入参数自适应律，使系统能够抑制干扰.采用该控制方法，进行大椭圆轨道慢旋目标同步绕飞跟踪控制器设计.仿真结果表明，该方法具有较强的鲁棒性以及良好的跟踪性能.

慢旋目标；椭圆轨道；积分滑模控制；自适应控制

大部分失控和被废弃卫星往往首先处于缓慢翻滚状态，并且随着能量的耗散最终将绕最大惯量轴慢旋.航天器利用机械臂抓捕旋转目标非常困难，如1997年11月的STS-87任务中，航天飞机遥操作系统抓捕 2（°）／s自旋的斯巴达卫星失败［1］.同步绕飞方式抓捕慢旋稳定非合作目标，追踪航天器超近距离绕飞需较高跟踪控制精度.有很多学者对两个航天器之间的相对位置控制问题进行了研究［2-3］，但文中大都假定目标运行在圆轨道上，且采用的模型为CW方程.为了完成某些空间科学和军事任务，航天器需要运行在椭圆轨道上.由于描述椭圆参考轨道相对位置运动的Lawden方程中的参数为时变量，且变化幅度较大，使得控制器设计难度大.文献［4］利用Lawden方程设计的二次线性最优控制为时变反馈控制，计算量大.并且目标是非合作的，期望相对速度、加速度信息难以获取，从而加大了跟踪控制器设计难度.

变结构控制作为一种先进的控制策略，可以使系统对包括外部干扰及内部参数扰动在内的不确定因素产生强鲁棒性.文献［5-7］对参数自适应变结构进行了研究，其中文献［5］针对满足匹配条件而不确定部分上界不确知的动态系统设计了自适应变结构控制器.在此基础上，本文对该方法作进一步改进，从调节系统拓展到多输入多输出跟踪系统，并实现了系统解耦.然后通过在滑模变结构控制中引入积分控制项，消除了传统滑模变结构控制要求被跟踪信号导数已知的条件.本文采用该方法，设计了大椭圆轨道慢旋目标同步绕飞跟踪控制器.仿真结果验证了该方法的合理性.

1 自适应积分滑模控制律设计

考虑如下系统：

假设系统满足以下条件：

假设1.系统满足如下匹配条件：

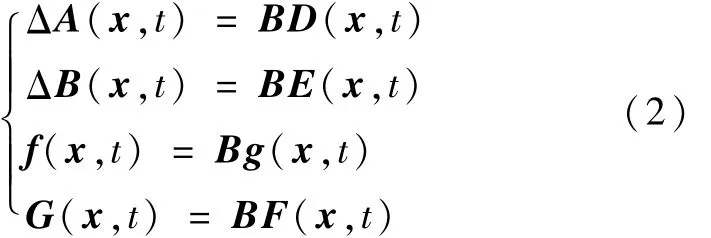
使得系统能够转化为如下形式：

式中，

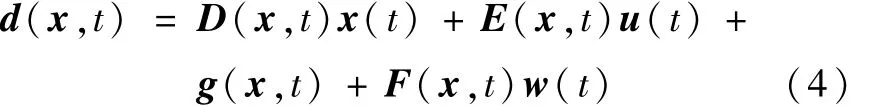
表示多种不确定性的总和.

假设 2.不确定性 d（x，t）满足

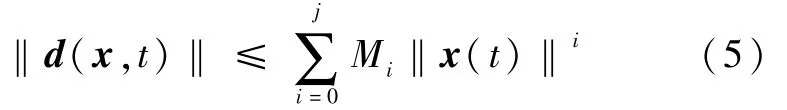
式中Μi是未知有界常数.

针对满足以上假设的系统，为了消除控制器中需要被跟踪信号的各阶导数项，在切换函数中引入跟踪误差的积分项［8］，并用各状态变量代替各误差项，定义切换面为

式中，K I＝diag｛kI1，…，kIm｝，C∈Rm×n满足CB可逆且在系统状态到达切换面s＝0后系统稳定，关于矩阵C的给定将在下面进一步讨论.设计控制律为

式中，

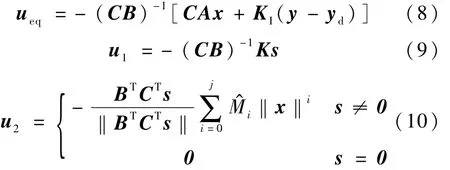
式中，K为正定矩阵；为假设2中未知有界常数Mi的自适应参数，并且自适应律为

定理1.对于给定的系统式（1），在满足假设1、2的情况下，使用控制律式（7）～式（10）和自适应律式（11），可以使得系统从任意初始状态到达切换面.证明.预选Lyapunov函数

对上式求导

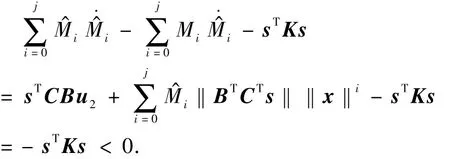
可见，切换动态是渐近稳定的.系统从任意初始状态出发，均能收敛到切换面.

控制律中u2存在跳变，引起了抖振.为了消除抖振，一种简单的处理方法是将开关函数连续化，在切换边界附近增加小的边界层，使得跳变转化为缓变.取

Δ为常数（Δ＞0），Δ越小，连续化后的函数越接近开关函数，控制效果越好，但消除抖振效果越弱.故应在控制效果和消除抖振之间权衡，合理选择Δ的值.

下面讨论如何选择参数使得系统在切换面s＝0上能有效跟踪.定义矩阵C为

式中，

到达切换面s＝0后，由˙s＝0可得

系统的特征方程为

由于特征方程不受系统参数变化以及外部干扰的影响，并在保证CB可逆的情况下可以任意选择参数.所以合理的选择参数，可以达到较理想的控制效果，使跟踪误差稳定在较小的值上.

2 超近距离绕飞模型分析

在惯性坐标系下，慢旋目标和追踪航天器的轨道动力学方程分别为

式中，μ为地球引力常数，rti和rci为慢旋目标和追踪航天器距地心的位置矢量，ati和aci为目标和追踪航天器除地球中心引力以外的其他作用力的合力加速度矢量，即推力和摄动力（包括地球形状摄动、大气阻力摄动和光压摄动等）的加速度矢量.

定义目标轨道坐标系：x轴和z轴在目标轨道平面，z轴由目标质心指向地心，x轴垂直 z轴并指向飞行方向，y轴与x轴、z轴右手正交.在目标轨道坐标系下，目标轨道角速度为ωto，追踪航天器和目标之间的相对位置矢量为 ρto＝rcto－rtto.

目标轨道坐标系下相对运动动力学方程为

其中，

式中，exto，eyto，ezto为目标轨道坐标系中各坐标轴单位矢量，ωto为目标角速度的大小.在ρ很小的情况下，在上式中可以略去及其更高幂次项，则有以下近似式：

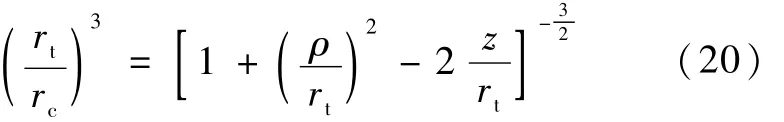
从而有

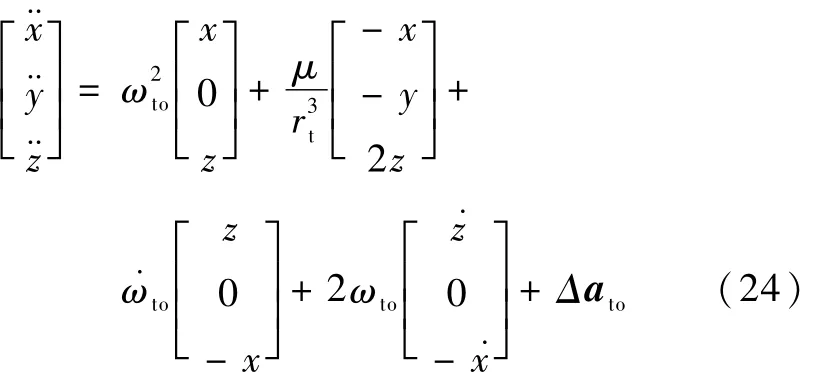
式中，Δato＝aconto＋adto包含追踪航天器控制推力加速度aconto和两航天器摄动加速度之差 adto.系统参数为

由于大椭圆轨道偏心率et较大且真近点角ft为时变量，使得系统参数在较大范围内变化，增加了控制难度.记

可以将系统状态方程写成如下简明形式：

式中，x＝［x˙x y˙y z˙z］T，u＝aconto，

系统具有形如式（3）的形式，满足假设条件1.

对于轨道高度120 km以下，大气阻力过大，轨道已无环绕意义.不失一般性，假定 rt＞6 498 km，0≤et＜1，经过演算可得：

从而不确定项

满足假设条件2.

3 仿真算例与分析

非合作目标绕最大惯量轴稳定慢旋，要求追踪航天器保持同步绕飞，绕飞面垂直于最大惯量轴.利用下面的姿态动力学方程和运动学方程［9］近似模拟慢旋目标的运动

转动角速度初值

姿态四元数初值

从描述目标姿态动力学方程可以看出，目标绕本体z轴慢旋.假定期望的相对位置在目标本体坐标系中表示为［5 0 0］Tm，垂直于自旋轴.

慢旋目标的轨道参数为：半长轴at＝13800 km，偏心率 et＝0.5，轨道倾角 it＝97.4°，近地点幅角 ωt＝90°，升交点赤经 Ωt＝0，且卫星经过近地点的时刻 tp＝0.设计切换面

可得 CB＝diag｛1，1，1｝可逆，各方向的传递函数为

系统渐近收敛.

在目标轨道坐标系中，相对位置和速度初值为：［－4 3 2］Tm，［0.2 0.4 0］Tm／s，干 扰 为0.0001［1＋sin（0.0011t）］m／s2.选择自适应参数初值 M＾00＝M＾10＝0，在不考虑测量噪声的情况下，仿真结果见图1～图2.

从仿真结果可以看出：绕飞面垂直于慢旋目标的自旋轴，轨道坐标系中表示的期望相对位置信号为较大幅值和频率的正弦曲线（如x轴方向期望轨线为幅值约5 m，周期约65 s的正弦曲线），系统成为跟踪控制系统；针对慢旋目标轨道为大椭圆轨道，系统参数较大范围变化的特点，设计的自适应积分滑模控制律能够使得追踪航天器有效跟踪期望相对位置信号；自适应参数，收敛到常数，从而估计出了系统不确定性范数‖d‖的上界，并且通过u2的作用，有效地抑制了系统的不确定部分造成的扰动.

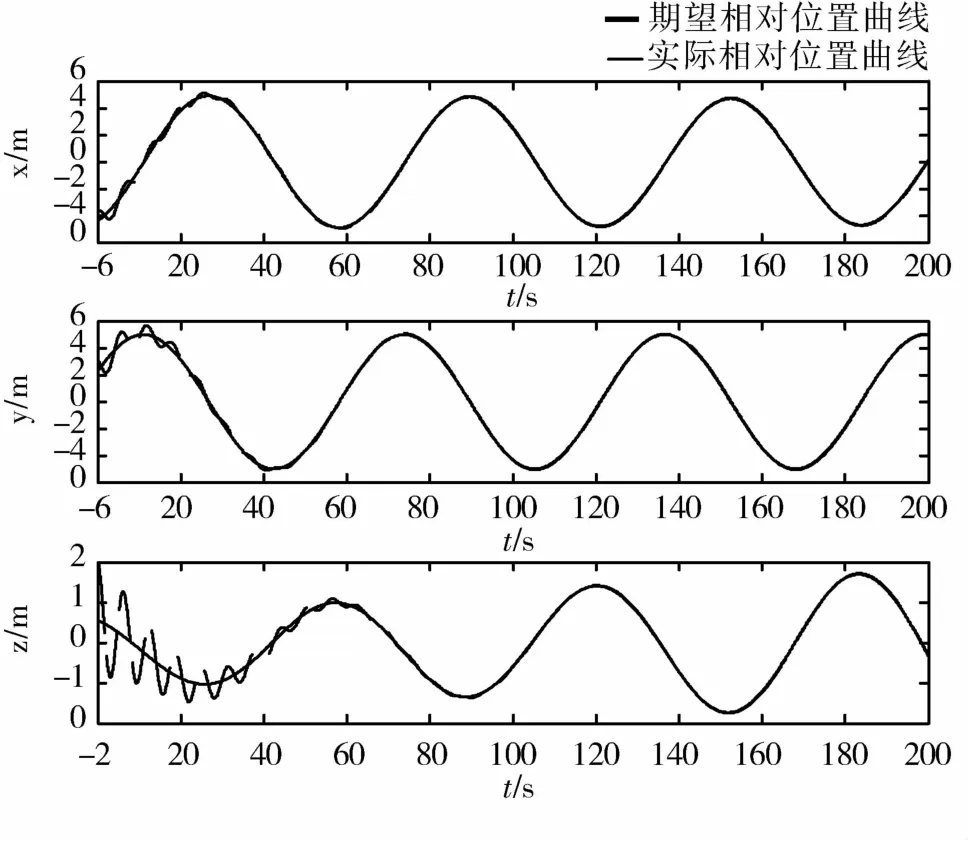
图1 期望和实际相对位置的仿真曲线

4 结 论

针对大椭圆轨道慢旋非合作目标绕飞跟踪控制问题，本文提出了一种参数自适应积分滑模控制策略.对于这类不确定部分上界不确知的系统有很好的跟踪控制效果，并且在切换函数中引入跟踪误差的积分项消除了传统滑模变结构控制所需的被跟踪信号一阶及高阶导数己知的假设，控制算法和自适应律也都较为简单.仿真结果显示，该控制方法具有很好的跟踪控制性能及较强的鲁棒性，可用于慢旋目标绕飞控制.

［1］Masumoto S，Ohkami Y，Wakabayashi Y，et al.Satellite capturing strategy using agile orbital servicing vehicle，Hyper-OSV ［C］.The 2002 IEEE International Conference on Robotics＆Automation，Washington DC，USA，May 2002

［2］卢山，徐世杰.卫星远距离伴飞的变结构控制［J］.航天控制，2007，25（6）：56-61

［3］Souza C.An optimal guidance law for formation flying and station-keeping［C］.AIAA Guidance，Navigation and Control Conference and Exhibit， Monterey，California，Aug 2002

［4］崔海英，李俊峰，高云峰.椭圆参考轨道的卫星编队队形保持控制设计［J］.工程力学，2007，24（4）：147-151

［5］李辉，谢剑英.不确定系统的参数自适应变结构控制［J］.上海交通大学学报，2000，34（5）：715-718

［6］Yoo D S，Chung M J.A variable structure control with simple adaptive laws for upper bounds on norm of uncertainties［J］.IEEE Transactions on Automatic Control，1992，37（6）：860-864

［7］Ahn C，Kim Y，Kim H.Adaptive sliding mode control for non-affine nonlinear vehicle systems［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Hilton Head，South Caroline，Aug 2007

［8］Lee J H，Allaire P E，Tao G，et al.Integral slidingmode control of a magnetically suspended balance beam：analysis，simulation and experiment［J］.IEEE／ASME Transactions on Mechanics，2001，6（3）：338-346

［9］Masumoto S，Dubowsky S.Fly-by approach and guidance for uncontrolled rotating satellite capture［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Texas，Aug 2003

Integral Sliding Mode Control with Adaptive Parameters for Flying around Slowly Rotating Target

LIU Zhiyong1，2，HE Yingzi1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

This paper presents an integral sliding mode control with adaptive parameters for a class of systems satisfying some conditions when the upper bounds of uncertainties are unknown.The switching function includes the integral of tracking error to avoid assuming that the derivative of desired signal must be known in conventional sliding mode variable structure control.This control approach uses the parameter adaptive algorithm based on the Lyapunov method to make the system reject disturbances.The proposed method is applied to slowly rotating non-cooperative target in an arbitrary elliptical orbit synchronous fly-around position tracking control.Simulation results indicate that the control approach is robust and improves the tracking accuracy considerably.

slowly rotating target；elliptical orbit；integral sliding mode control；adaptive control

V448.2

A

1674-1579（2009）04-0022-05

*863计划（2007AA704037）资助项目.

2008-11-29

刘智勇（1984—），男，江西人，硕士研究生，研究方向为航天器姿态轨道控制 （e-mail：liuzy502＠163.com）.