基于指数趋近律的高超声速飞行器滑模控制器设计

李惠峰，孙文冲

（北京航空航天大学，北京 100191）

令：

则方程式（10）和（11）可以写成向量形式

基于指数趋近律的高超声速飞行器滑模控制器设计

李惠峰，孙文冲

（北京航空航天大学，北京 100191）

采用NASA兰利实验室开发的一种通用高超声速飞行器的改良非线性纵向模型，针对输入／输出线性化模型，以指数趋近律作为到达条件设计滑模变结构控制器，该方法能够较好地处理不确定性问题，而且对外界干扰不敏感.仿真在高超声速巡航条件下进行，通过对跟踪高度和速度阶跃指令的仿真验证，并与符号函数作为到达条件设计的滑模控制器进行对比，发现前者在速度阶跃和高度阶跃响应速度上较后者分别提高了50%和70%左右，并且以符号函数设计的滑模控制器存在稳态误差，而以指数趋近律作为到达条件设计的滑模控制器可以达到0误差的跟踪精度.

高超声速飞行器；滑模控制；趋近律；鲁棒性

高超声速飞行器的控制问题是近年研究的一个热点，由于高超声速飞行器飞行包线大，飞行环境复杂多变，以及飞行器机身与推进系统严重耦合［1］，其动力学模型具有高度的非线性和不确定性，经典控制理论已经很难保证高超声速飞行器的控制系统既满足鲁棒性［2］又满足性能指标的要求.

目前用于飞行器的控制方法主要有动态逆控制、最优控制、基于遗传算法的模糊控制、滑模变结构控制等.动态逆控制方法［3］需要精确的数学模型，但高超声速飞行器模型具有较大的不确定性，随着模型不确定性的加大，动态逆的控制效果会下降.最优控制对于低阶的系统可以取得较好的控制效果，但对于高维系统，求解 Riccati方程需要花费大量的计算时间，计算花费时间随着维数的增加而迅速增长，这是这种方法的致命弱点，也是这种方法在被提出后的几年来应用较少的原因，高性能的计算机有助于解决这个计算问题.基于遗传算法的模糊控制优点在于不需要精确的数学模型［4］，能够较好地处理非线性问题，但这种控制方法需要大量的专家经验，而且遗传算法的寻优计算量大，比较耗时.滑模控制方法能够较好地解决模型不确定问题［5］，并且这种方法对系统的外界干扰不敏感［6］，是解决高超声速飞行器控制器设计的一个较好的方法.

1 高超声速飞行器纵向动力学模型

本文采用通用高超声速飞行器六自由度动力学模型［7］，即

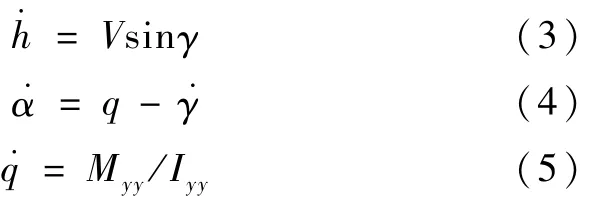
CM（δe）＋CM（q）］，r＝Re＋h，升力系数 CL＝0.620 3α，阻力系数 CD＝0.645α2＋0.004 337 8α＋0.003 772，推力系数

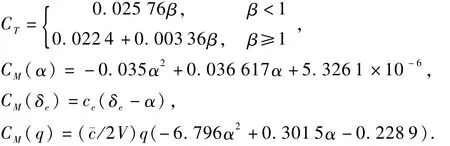
发动机动态方程采用二阶系统模型

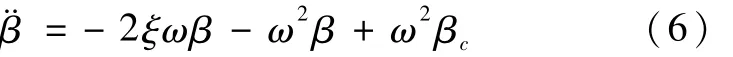
在假定的参数额定值中加入随机变化量来表示参数的不确定性，表示如下：

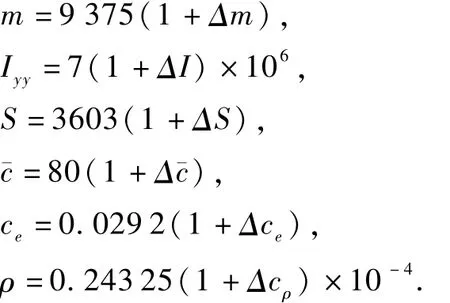
模型分析：

由模型方程可见，此模型具有高度非线性，而且气动参数和状态相互耦合，并且一部分系统参数存在不确定性，故此系统为非线性时变不确定系统，其控制器的设计十分困难，目前还没有一种系统化的方法为此类系统设计控制器，本文的设计思路为先将模型进行全状态反馈线性化，然后采用滑模变结构控制方法进行控制器的设计.

本文以控制飞行器的速度和高度为目的，控制输入为节流阀设置βc和升降舵偏角 δe，通过设计 βc和δe的值来控制速度V和高度h，以跟踪速度阶跃指令和高度阶跃指令.在精确模型和不确定模型的情况下进行仿真，以验证控制器的可靠性和鲁棒性.

2 模型线性化

选择状态向量 x＝［V γ α β h］T，控制向量为u＝[βcδ]e，由于本文研究的是速度阶跃跟踪和高度阶跃跟踪，故对速度和高度方程进行线性化.根据完全反馈输入／输出线性化理论，对速度和高度进行微分，直到出现不为0的控制输入分量系数，通过对V三次微分和对h四次微分得

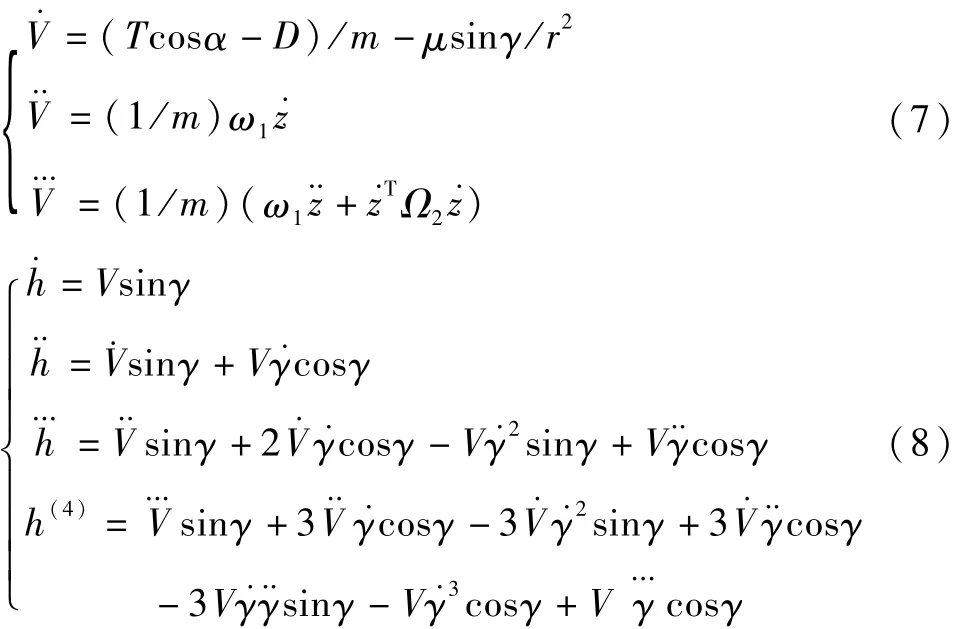
并且，

式中，

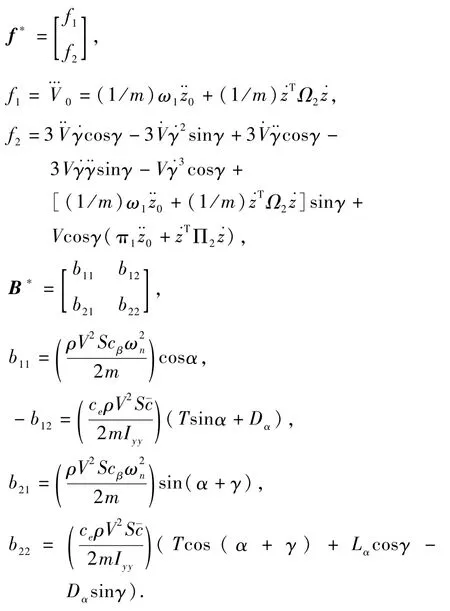
可见，经过通过对V三次微分和对h四次微分可以出现控制输入量，进而可以对模型的速度通道和高度通道进行线性化，并以此设计滑模控制器.

3 滑模控制器的设计

3.1 滑模控制简介

滑模控制是近年来发展较快的一种控制方法，滑模控制器的设计包括设计滑模面和到达条件.滑模面一般是根据性能指标的要求定义的，滑模面的定义要保证当系统滑动模态（一般为待控状态量）收敛到滑模面上时，系统的性能指标达到要求.所以滑模控制的任务是设计控制器使系统滑动模态最终收敛到滑模面上并且保持在滑模面上运动.

3.2 定义滑模面

控制器的设计主要是完成速度和高度的跟踪，因此定义两个滑模面分别进行速度通道和高度通道的控制.结合速度高度线性化过程可将滑模面定义如下：

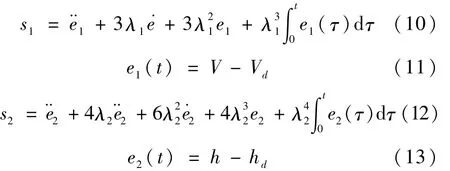
其中λ1，λ2是定义误差动态带宽的两个严格正常数.滑动面si＝0，i＝1，2表示一个线性微分方程，其解意味着分别以时间常数 2／λ1，3／λ2指数的衰减到接近于0，跟踪误差的积分项用来消除稳态误差.

1

2

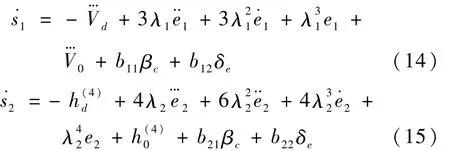
3.3 到达条件

到达条件的设计必须保证滑动模态在有限时间内收敛到滑模面上并保持在滑模面上运动.即需要满足s·˙s＜－a，其中a是一个正常数.目前研究较多的是符号函数到达条件，文献［10］就是用的这种方法设计的滑模控制器，为消除抖振，这种方法还需定义一个边界层，但边界层的存在会降低系统的响应速度，并且导致稳态误差的产生.针对符号函数到达条件的上述缺点，本文采用指数趋近律作为到达条件设计滑模控制器，有效解决了跟踪速度慢和存在稳态误差的问题，并且具有较强的鲁棒性.

指数趋近律设计如下：

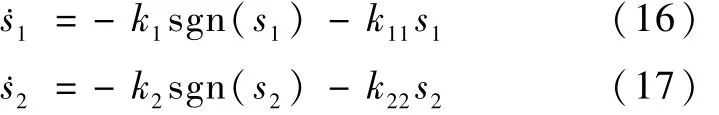
上式中k1、k2可以保证系统在有限的时间内到达滑模面，但过大的 k1、k2又会引起抖振，故 k1、k2的值要小一些，其作用相当薄边界层.k11、k22可以选择的大一些，可以加快系统的响应速度.通过调节 k1、k11、k2、k22既可以保证滑动模态到达过程的动态品质，又可以减弱控制信号的高频抖振.

3.4 滑模控制器

将方程（10）～（15）代入式（16）和（17），考虑到 －和 －项均为0得

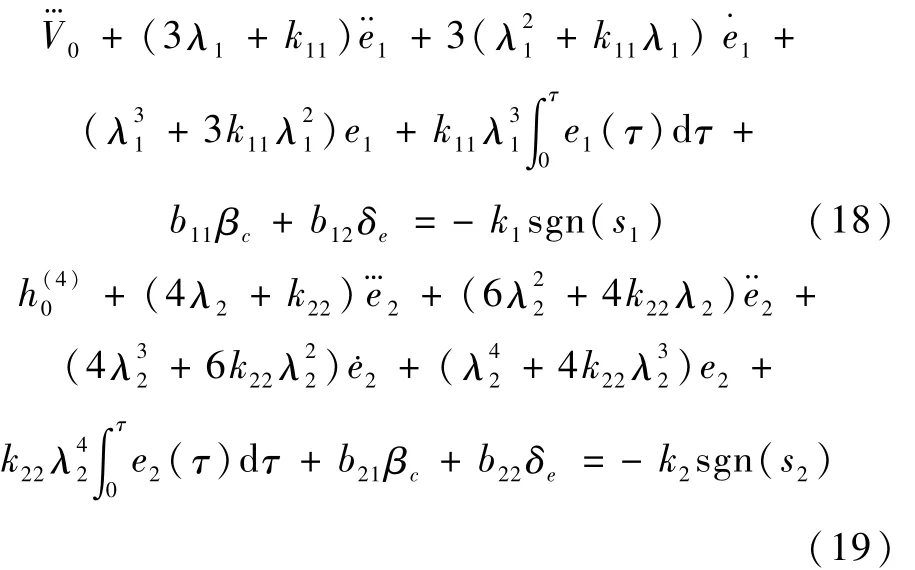
令：

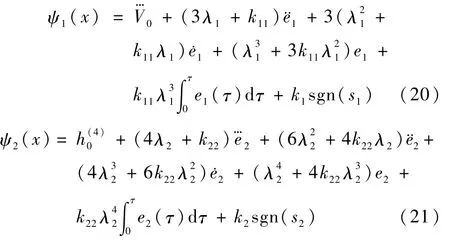
则方程式（10）和（11）可以写成向量形式

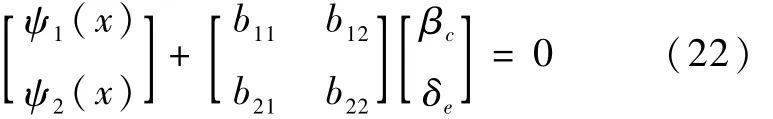
因为飞行器飞行轨迹不可能是垂直的，即航迹角不可能为90°，容易证明：

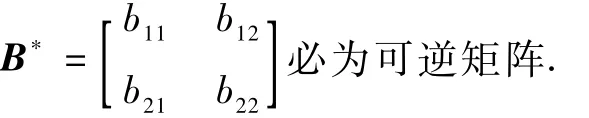
故可以求得控制向量为

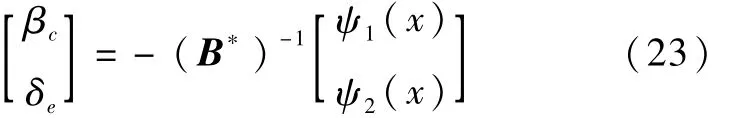
4 仿真分析

反复调节控制器中 λ1，λ2、k1、k11、k2、k226个可调参数，直至仿真结果收敛，初始巡航条件为：V＝4 590.3 m／s，h＝33 528 m.

仿真结果如图1～图3.

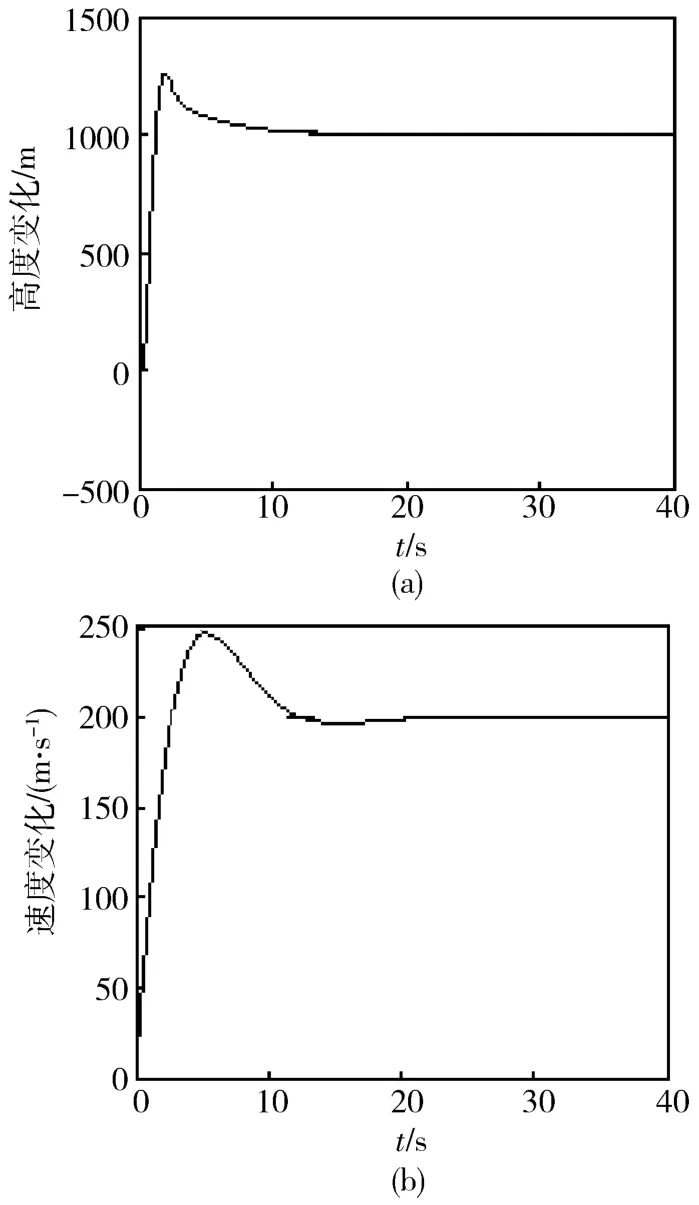
图1 标称模型对1 000 m高度阶跃指令和200 m／s速度阶跃指令的响应（采用指数趋近律到达条件）

不确定性仿真：

为了检验控制器的鲁棒性，在标准模型中加入不确定性进行仿真，不确定性的加入通过在6个不确定参数中加入一项随机函数来实现，随机函数取值范围为0～1，系数为0.2，加20%不确定性时的仿真结果如图3.

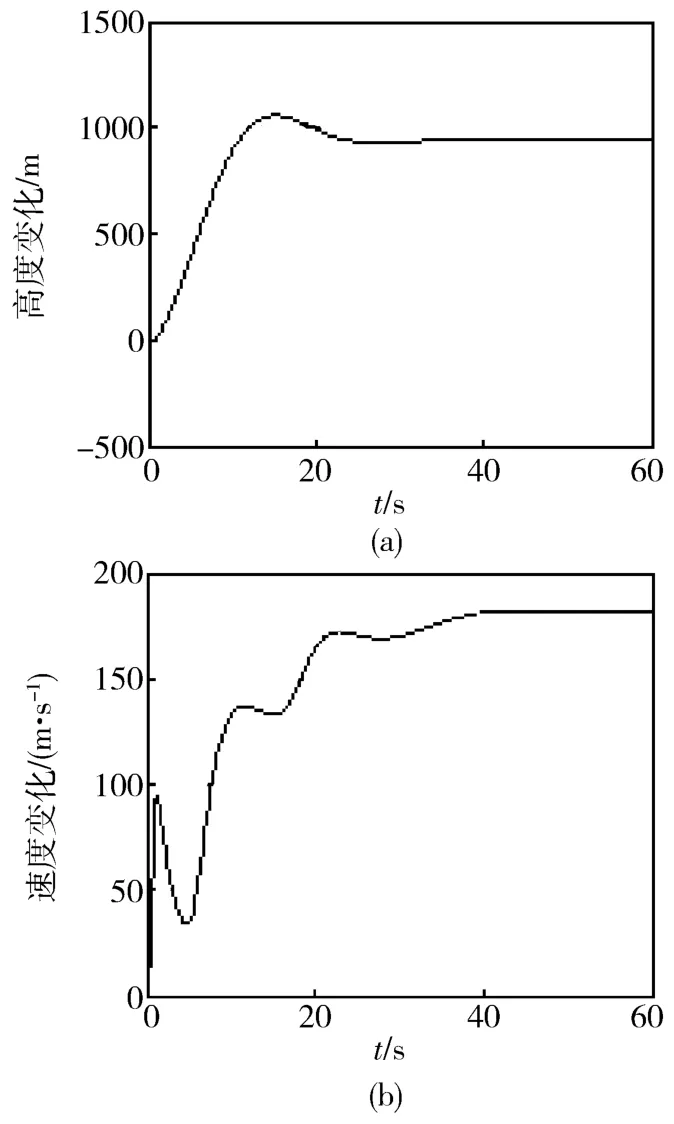
图2 标称模型对1 000 m高度阶跃指令和200 m／s速度阶跃指令的响应（采用符号函数到达条件）

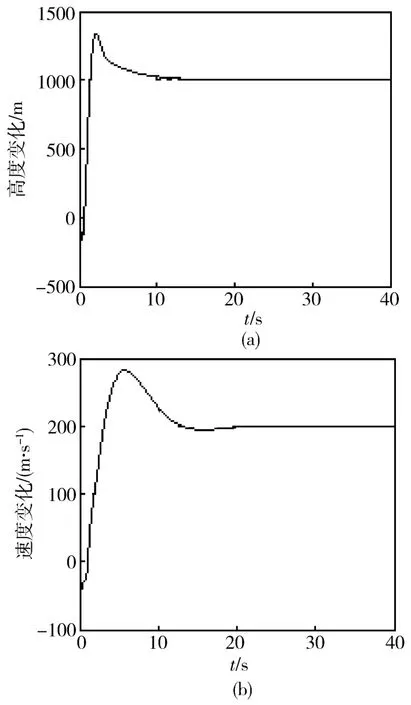
图3 不确定性模型同时对1 000 m高度阶跃指令和200 m／s速度阶跃指令的响应

图1 为采用指数趋近律时标称模型对1 000 m高度阶跃指令和200 m／s速度阶跃指令的仿真图，图2为采用符号函数到达条件时标称模型对1 000 m高度阶跃指令和200 m／s速度阶跃指令的仿真图，两组图对比可以发现，采用两种到达条件都能达到较好的控制效果，但采用指数趋近律设计的滑模控制器在跟踪速度和跟踪精度上都要优于采用符号函数作为到达条件设计的滑模控制器.图3为加20%不确定性后采用指数趋近律作为到达条件的仿真图，由图可以看出，在较大的不确定性情况下，控制器仍能实现较好的跟踪，验证了控制器具有良好的鲁棒性.

5 结 论

本文针对通用高超声速飞行器纵向模型，采用指数趋近律作为到达条件，设计了滑模控制器，滑模控制器具有良好的跟踪性能和优良的鲁棒性，对高超声速飞行器高度阶跃指令和速度阶跃指令具有很快的跟踪速度和很高跟踪精度.指数趋近律作为到达条件是一种较好的消抖措施，能够提高系统的快速性、稳定性以及精确性，并且提高了系统的鲁棒性.

［1］朱云骥，史忠科.高超声速飞行器飞行特性和控制的若干问题［J］.飞行力学，2005，23（3）：1-6

［2］Wang Q，Robert F S.Robust nonlinear control of a hypersonic aircraft［R］.AIAA-99-4000，1999

［3］刘燕斌，陆宇平.非线性动态逆控制在高超飞控系统中的应用［J］.应用科学学报，2006，24（6）：127-134

［4］王美仙，李明，张子军.飞行器控制律设计方法发展综述［J］.飞行力学，2007，25（2）：324-331

［5］刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展［J］.控制理论与应用，2007，24（3）：382-388

［6］Xu H J，Mirmirani M.Robust adaptive sliding control for a class of MIMO nonlinear systems［R］.AIAA-2001-4168，2001

［7］Marrison C I，Stengel R F，Design of robust control system for a hypersonic aircraft［J］.Journal of Guidance，Control and Dynamics，1998，21（1）：58-63

［8］程代展.应用非线性控制［M］.北京：机械工业出版社，2006

［9］张晓宇，苏宏业.滑模变结构控制理论进展综述［J］.化工自动化及仪表，2006，33（2）：1-8

［10］Xu H J，Petros A I，Majdedin M.Adaptive sliding mode control design for a hypersonic aircraft vehicle［R］.CATT Technical Report，02-02-01

［11］Xu H J，Mirmirani M，Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynamics，2004，27（5）：829-838

Exponential Approach Law Based Sliding Control for a Hypersonic Vehicle

LI Huifeng，SUN Wenchong
（Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

A universal improved nonlinear longitudinal model of a hypersonic vehicle developed by the Langley lab is adopted.For its I／O linearized model，a sliding mode controller is designed.This method can solve the uncertainty problem and it is insensitive to disturbances.The exponential approach law used to drive the sliding mode to reach the sliding surface is adopted to eliminate the quiver.The simulation results for tracking the height step and velocity step order at cruise condition show that the sliding mode controller with index approach law acquires satisfying tracking ability and strong robustness.The controller can not only track the single height step order or velocity step order accurately，but track the height step order and velocity step order together fleetly with zero error.In addition，the sliding controller with exponential law is better than the one with sign function in tracking speed and precision.Another result is also proved that the index approach law can eliminate the quiver perfectly.

hypersonic vehicle；sliding mode control；approach law；robustness

V4

A

1674-1579（2009）04-0039-05

2008-12-06

李惠峰（1970—），女，陕西人，副教授，研究方向为高速飞行器制导与控制、离散事件系统理论和混合系统理论（e-mail：lihuifeng＠buaa.edu.cn）.