混凝土水化热对联络通道冻土帷幕的影响

肖朝昀

(华侨大学土木工程学院，福建 厦门 361021)

胡向东

同济大学土木工程学院地下建筑与工程系，上海200092同济(大学岩土及地下工程教育部重点实验室，上海200092)

混凝土水化热对联络通道冻土帷幕的影响

肖朝昀

(华侨大学土木工程学院，福建 厦门 361021)

胡向东

同济大学土木工程学院地下建筑与工程系，上海200092同济(大学岩土及地下工程教育部重点实验室，上海200092)

利用有限差分方法，分析隧道联络通道结构施工时混凝土水化热对人工冻结形成的冻土帷幕的影响。混凝土水化热的释放使得混凝土内温度急剧上升，之后受冻土帷幕低温和混凝土永久支护边界散热的影响，温度逐渐下降。混凝土水化热大量释放期间，冻土帷幕局部升温并融化，相界面移动迅速，并达到最大值。之后温度回落，经过几天的降温后，冻土开始回冻，冻土帷幕回冻速度比较缓慢。分析结果表明，常见的盾构隧道联络通道结构浇注的混凝土始终不会进入负温状态，混凝土不会因为冻土帷幕低温影响遭受冻害。

有限差分法; 混凝土水化热; 冻土帷幕; 人工冻结; 冻害

运用人工冻结法施工的隧道联络通道工程中，浇注永久支护时，混凝土将产生大量的水化热，会影响已经达到稳定状态的冻土帷幕，冻土帷幕内温度会在一定范围内升高。同时，冻土帷幕回冻后又会导致混凝土内温度降低。工程界关注的有2方面，一方面，混凝土水化热削弱冻土帷幕程度大小；另一方面，冻土回冻是否会导致混凝土处于低温状态，进而影响混凝土性能。

要回答上述问题，必须对冻土帷幕温度场进行分析。冻土帷幕温度场是一个含相变的瞬态导热问题，属于移动边界问题(Stefan问题)[1]。这类问题的基本特点是边界未知且移动，即固相和液相被一个两相的移动区域所分离。求解这类问题主要有解析法、近似法和数值方法。解析法得出问题的精确解只限于一些半无限大或无限大区域，且具有简单的边界条件与初始条件的一些理想化情形。对于复杂边界条件的移动边界问题，寻找适当的解析方法十分困难。而数值法则在近年来又有了新的进展，尤其表现在相变的处理技术上。文献[2,3]采用有限差分方法对人工冻结温度场进行分析；文献[4]针对土壤冻结过程的数值分析，基于显热容法用有限差分法构造出热传导方程变空间步长的半隐格式和全隐格式；文献[5]采用解析法和差分法相结合的方法，分析了立井冻结过程中冻土交圈前和交圈后温度场分布；文献[6]应用二维有限元方法分析、计算地层人工冻结过程，对传热过程中相变潜热的处理提出了简便，有效的方法，这些方法普遍适用于含有潜热的非线性二维热传导问题；刘中良[7]介绍了求解一维常物性移动边界问题的MVTS方法，对其迭代方法作了较彻底的改进，大大减少了计算时间。

鉴于计算冻土帷幕非线性、非稳定性温度场分布的复杂性，笔者就上述2方面问题，利用前人的研究成果，把具有相变的冻土帷幕温度变化问题简化为一维数学问题，利用差分法建立了数值模型，对混凝土水化热致使冻土帷幕温度场分布变化的规律进行研究。

1 数学模型

1.1控制方程

图1为混凝土水化热对冻土帷幕温度场影响计算模型示意图。记冻土帷幕单侧厚度为H，混凝土永久支护厚度为D。

将冻土帷幕划分为固相和液相2个区域，相界面两侧固相和液相的数学描述为[1]：

式中，Ts、Tl为固相和液相的温度；αs、αl为固相和液相的导温系数；X(τ)为相界面位置。

界面x=X(τ)处的耦合条件为：

Ts(x,τ)=Tl(x,τ)=Tf

(3)

(4)

式中，Tf为相变温度；L为相变潜热；ks、kl为固相和液相的导热系数；ρ为密度。

混凝土永久支护区为具有内热源的一维非稳态导热问题，其控制方程为：

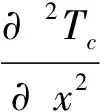
(5)

式中，Tc为混凝土内温度；αc为混凝土导温系数；qc为单位时间内单位长度的混凝土释放的热量。

1.2初始条件和边界条件

初始时刻τ，冻土帷幕具有特定的温度分布f(x)，并且初始相界面位置在x=H处，初始条件为：

Ts(x,τ)=f(x) 0≤x≤H

(6)

X(τ)=H

(7)

τgt;0时，边界条件为：

式中，T0为冻结管附近冻土帷幕温度。

在x=H+D处，对流边界条件为：

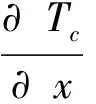
(10)

式中，kc为混凝土导热系数；h为散热系数；Ta为空气温度。

1.3混凝土水化热

描述混凝土水化放热有双曲函数和指数函数[8,9]，其中指数形式为：

Q(τ)=Q01-e-a(τ/24)bτgt;0

(11)

式中，Q(τ)为龄期τ时的累积水化热；Q0为τ趋近无穷大时的最终水化热；τ为龄期；a、b是常数，与水泥品种、比表面积及入模温度有关。

在Δτ时间内混凝土水化放热的函数关系式为：

q(τ)=WQ1{e-a(τ/24)b-e-a[(τ-Δτ)/24]b}

(12)

式中，q(τ)为单位时间内每立方米混凝土水化放热量；W为水泥用量。

2 数值实现

采用克拉克-尼科尔松(Crank-Nicolson)格式[10]，式(1)、(2)可离散为：

(13)

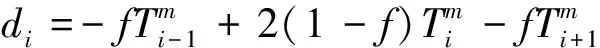
对于含内热源的一维非稳态导热方程式(5)，将式(12)代入，同样可离散为式(13)，但:

再将边界进行离散，其中对流边界条件式(10)可离散为：

(14)

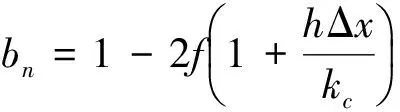
目前相变处理主要有显热容法和焓法[10]，笔者采用焓法进行处理，简述如下：

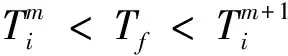
(15)

式中，Ti应为冻结温度Tf；ΔQm为时间Δτ内相变节点释放的热量；k值的选取将分别由节点i的邻近节点处于固态相还是液态相而定。运用式(15)的目的是计算ΔQm值。一个Δτ对应一个ΔQm。对式(15)经过若干次运算后，可达到下式所述条件：

(16)

式中，Q*为单元体的物质所具有的相变潜热，其值为LΔx；m′表示冻结过程进入相变阶段所对应的时刻τ。式(16)所示条件表明i节点相变完成。

离散后的差分方程如式(13)、(14)等可写成一封闭的代数方程组，利用追赶法求得各节点温度，进而求得各个区域温度分布，相界面X(τ)的位置也随之确定。

3 计算与分析

针对复兴东路越江隧道联络通道，其结构尺寸见图1，H=1m，D=0.55m，以冻结管中心线位置为坐标原点，指向永久支护为x轴正方向。土体的热性能参数见表1，混凝土热性能参数和水泥水化热常数见表2和表3，表中数值参照文献[8]。冻结管附近的冻土温度为-25℃，联络通道内由于作业密集，空气散热系数取h=15W/(m2·℃)，空气温度按15℃计算，相变温度Tf=-1℃。冻土内初始温度分布假定为直线分布，即x=0时，T=-25℃；x=1时，T=-1℃。计算过程中不考虑混凝土永久支护与冻土帷幕之间木背板的影响。木背板实际上起着削弱混凝土水化热对冻土帷幕的作用，因此，笔者对混凝土水化热对冻土帷幕影响的计算结果比实际值要大。

表1 土体热性能参数

表2 混凝土热性能参数

表3水泥水化热常数[8]

3.1混凝土内温度分析

图2为28d龄期内，每立方米混凝土每天水化放热量q(τ)。图中显示，混凝土前3d总释放的水化热占总水化热的73%，7d达到90%。混凝土前期释放大量的水化热致使混凝土内温度急剧上升。图3为计算出的混凝土3个不同位置温度随时间的变化曲线，分别为靠近冻土帷幕一侧、中心位置和表面散热一侧。混凝土入模温度取25℃。从图上可以看出，混凝土内最高温度接近40℃，之后由于混凝土内水化热强度减弱，以及空气散热的影响，混凝土内温度逐渐下降，3d内温度回落到20℃左右。由于边界散热以及受冻土帷幕回冻的影响，混凝土中心温度最终稳定在10℃左右。混凝土与冻土帷幕交界面处(见图3靠近冻土帷幕一侧曲线)，混凝土温度始终维持在0℃以上，表明混凝土不会进入负温状态。

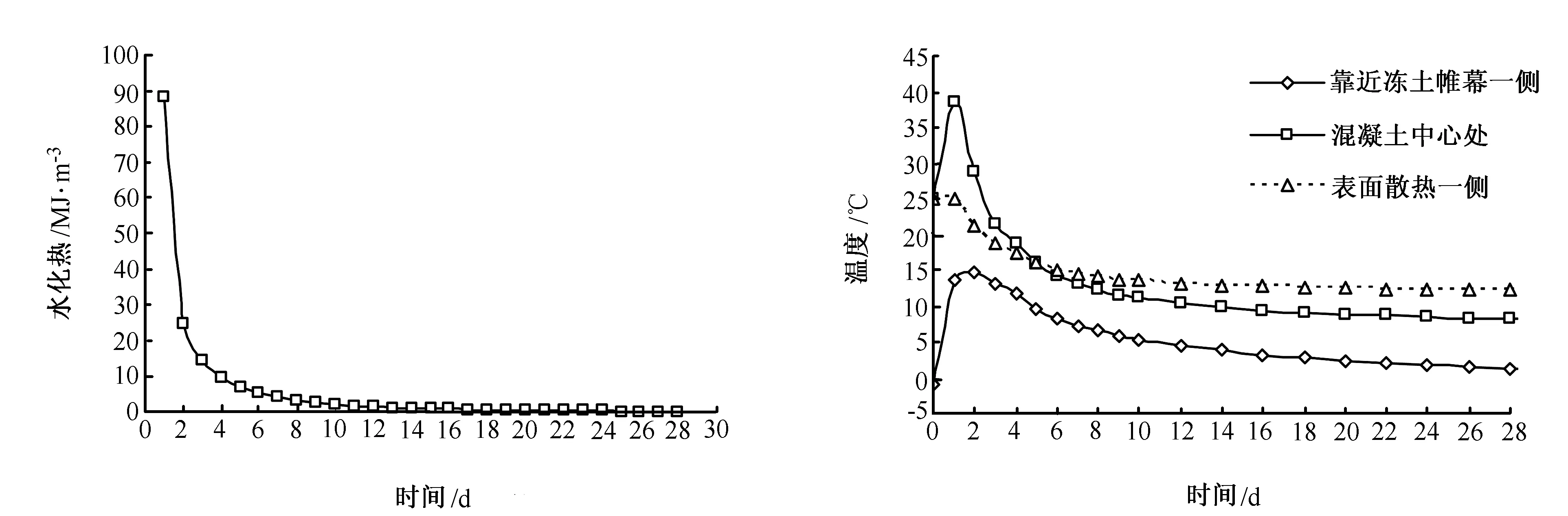
图2 混凝土水化热随时间变化曲线 图3 混凝土内不同位置温度变化曲线

3.2冻土帷幕内温度分析

由于受混凝土水化热的影响，越靠近混凝土表面的冻土帷幕受水化热影响越大。图4为1m厚冻土帷幕内不同位置温度随时间的关系曲线。最初3天，距离混凝土永久支护0.2m范围内冻土帷幕温度急剧上升，其最高温度可达15℃(见0.9、1m曲线)，之后温度开始回落。0.6～0.8m范围内冻土帷幕温度由前4d温度上升，经过几天的平台后，温度开始回落(见0.7、0.8m曲线)。从图0～0.6m范围内冻土帷幕受混凝土水化热影响很小，最高上升温度不超过2℃(见0.25、0.45m曲线)。

图5为相界面X(t)随时间的关系曲线。受混凝土水化热的影响，前3d相界面移动迅速，6d后达到最大值0.79m，之后冻土帷幕开始回冻，冻土帷幕回冻速度比较缓慢，一直到51d，相界面位置才接近最初位置。

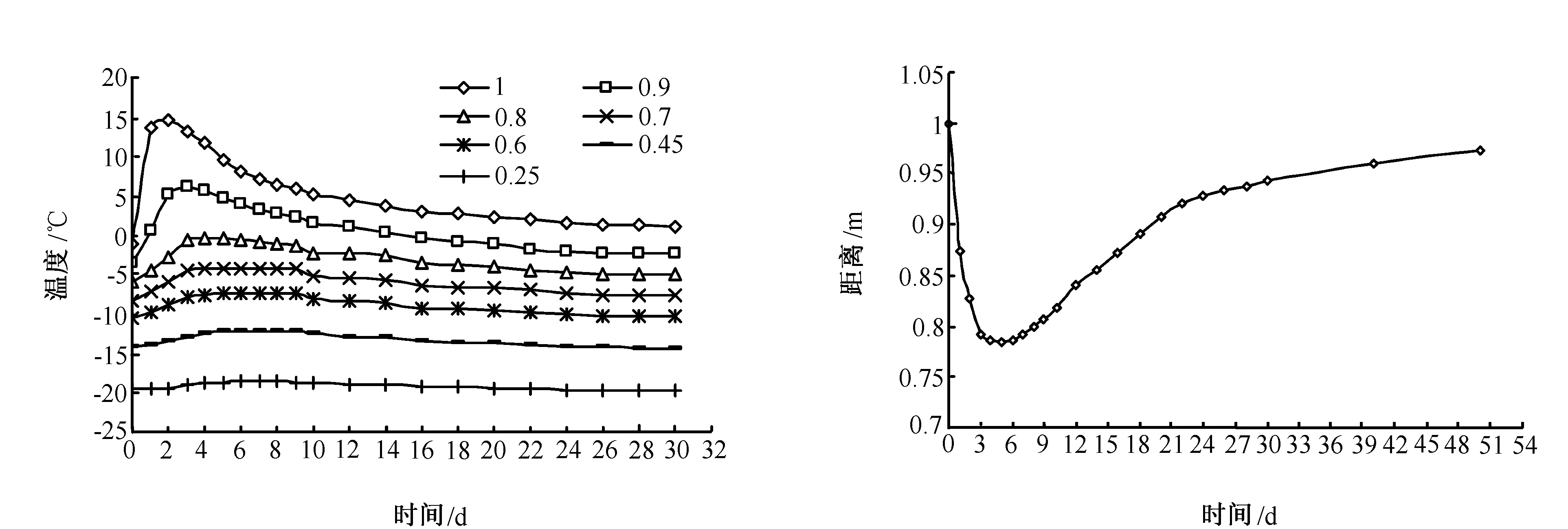
图4 冻土帷幕内不同位置温度变化曲线 图5 相界面位置随时间变化曲线

冻土帷幕受混凝土水化热影响程度主要由冻土帷幕有效厚度及平均温度决定。由以上分析可知，在整个混凝土水化热释放期间，冻土帷幕有效厚度均不低于0.79m。根据冻土帷幕有效厚度内各点温度，可计算出冻土帷幕平均温度。计算结果表明，在整个混凝土水化热释放期间，冻土帷幕平均温度在-15.5℃左右，上下变化幅度不超过0.5℃。计算过程中没考虑木背板的影响，木背板起着阻隔混凝土水化热向冻土帷幕传递的作用，实际工程中，混凝土水化热对冻土帷幕有效厚度削弱作用会更小。

4 结 论

笔者利用有限差分法分析混凝土水化热对冻土帷幕温度场的影响。分析了混凝土内、冻土帷幕内温度变化及其相界面移动与时间的关系，主要结论有：

1) 混凝土水化热的释放使得混凝土内温度急剧上升，之后受冻土帷幕低温和混凝土永久支护边界散热的影响，温度逐渐下降；

2) 混凝土水化热大量释放期间，冻土帷幕相界面移动迅速，并且达到最大值。经过几天的稳定后，冻土开始回冻。与解冻速度相比，冻土帷幕回冻速度比较缓慢；

3) 浇注的混凝土始终不会进入负温状态，混凝土不会因为冻土帷幕低温影响遭受冻害。

[1]奥齐西克.热传导[M]. 俞昌铭 译.北京: 高等教育出版社, 1983.

[2] 丁德文, 傅连弟, 庞荣庆. 冻结壁变化的数学模型及其计算[J]. 科学通报, 1982, (14): 875～879.

[3] 任松保, 郑正泉. 冻结过程中相变界面移动及传热的计算机模拟[J]. 华中科技大学学报, 2003, 31(2): 61～63.

[4] 商翔宇, 周国庆, 别小勇. 冻结土壤温度场数值模拟的改进[J]. 中国矿业大学学报, 2005, 34(2):179～183.

[5] Holden J T. Improved thermal computations for artificially frozen shaft excavations[J]. Journal of geotechnical and geoenvironmental engineering, 1997, 123(8): 696～701.

[6] 张燕, 干松水. 人工冻结壁形成及温度分布有限元分析[J]. 工程热物理学报, 1984, 5(2): 175～181.

[7] 刘中良, 潘延龄. 一维动边界问题的变时间步长方法[J]. 华东石油学院学报, 1986, 10(3): 28～39.

[8] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1991.

[9] 李东. 大体积混凝土裂缝控制 [D]. 西安: 西安建筑科技大学，1995.

[10] 张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社, 2006.

[编辑] 易国华

2009-08-16

国家自然科学基金项目(50578120)。

肖朝昀(1979-)，男，2000年大学毕业，博士，讲师，现主要从事岩土工程方面的研究。

TU472.9

A

1673-1409(2009)04-N086-05