基于CFBG的SSB调制系统研究

罗江华，陈海燕

(长江大学物理科学与技术学院，湖北 荆州 434023)

基于CFBG的SSB调制系统研究

罗江华，陈海燕

(长江大学物理科学与技术学院，湖北 荆州 434023)

研究了啁啾光纤光栅 (CFBG，Chirped Fiber Bragg Grating)的SSB调制系统。对光信号给予一定的色散补偿，能有效的实现单边带调制(SSB,Single Sideband)。并以高斯形载波光谱为例，对基于60GHz的副载波调制光信号进行了数值计算。结果显示，该滤波系统能够实现22dB边带抑制比和88km的色散预补偿。

啁啾光纤光栅；单边带调制；带通滤波器；色散补偿

ROF(radio over fiber)系统中传统的副载波双边带调制(SCM-DSB,Subcarrier Multiplexing-Double Sideband)中会产生2个边带的拍信号。具有相差的2个边带在接收机产生拍频后，2个射频信号将相互干涉，导致射频信号的衰减。当色散使得2个边带的微波信号产生了π的相差时，射频信号将完全抵消，而无法还原微波信息。单边带调制可以完全消除色散导致的载波抑制效应，使得接收端只产生一个射频信号。

诸多针对ROF系统中的单边带调制的实现方案被陆续提出,如利用双电极Mach-Zehnder调制器[1];利用窄带光纤光栅滤波法[2]；基于受激布里渊散射[3]等等。相比较，光纤布拉格光栅(FBG,Fiber Bragg Grating)拥有全光纤结构、良好光纤兼容性，低的插入损耗和潜在的低成本。因此，光纤布拉格光栅作为色散补偿元件有其无可比拟的优势。

考虑到引入啁啾后的FBG具有较大的反射带宽，在40G及以上副载波复用的ROF系统，利用其作为带通滤波器是合理的。为此，笔者研究了CFBG的SSB调制系统。

1 负载波DSB调制信号传输的理论分析

图1 光纤色散系统

光纤色散系统如图1所示。其中，LD表示载波光源，Xin(t)表示输入的副载波射频信号，经Mach-Zehnder调制器调制到光波上，经过光纤传输后，在接受端通过光电二极管直接探测出输出信号Xout(t)。如果忽略系统中的色散、非线性和损耗，则Xout(t)=Xin(t)。但是，在实际系统中必须考虑这些因素的影响，因此对光纤系统引入传输函数H(f)。

将光纤看成具有平坦振幅响应和线性的群时延响应的带通滤波器，不考虑光纤的损耗和高阶色散的影响，光纤传输函数[4]可以表示为:

H(f)=exp-jφ(f)=exp-jαf2

(1)

光纤系统中传递的信号在频域内可以表示为：

Yout(f)=Yin(f)H(f)

(2)

Yout(t)=F-1[Yout(f)]

(3)

其中，Yin(f)=F[Yin(t)]；Yout(f)=F[Yout(t)]；F[]和F-1[]分别表示傅立叶变换和反变换。在光纤系统中传输后的光信号最后经由光电检测器，由平方率定律最后输出信号可以表示为:

Xout(t)=|Yout(t)|2

(4)

下面，笔者对图1的系统进行定量的分析。

输入电信号Xin(t)经过Mach-Zehnder调制器[5]后输出光信号可以表示为:

Yin(t)∝J0(m)cos(ωct)-J1(m)[cos(ωc-ωrf)t+cos(ωc+ωrf)t]

(5)

代入式(2)和式(3)，经傅立叶变换和反变换后，由平方率定律(4)可得：

(6)

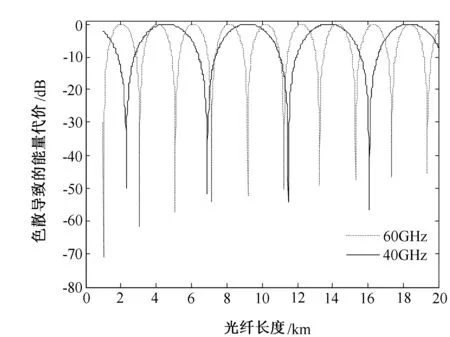
图2 色散导致的载波抑制现象

由于检测到的光电流正比于光功率，忽略直流成分，检测到的射频(RF,radio frequency)电信号功率Prf可以表示为：

(7)

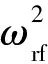
光电接收机检测到的信号功率随光纤长度以及调制频率变化规律见图2。由图2可以看出，接收机检测到的信号能量沿着光纤长度方向做周期性变化，射频信号的频率不同时，变化周期也不同。

2 CFBG反射谱和时延特性

光纤光栅折射率变化[6]可以表示为：

(8)

图3 啁啾光纤光栅的反射谱和时延曲线

对于CFBG，其反射率无解析解，笔者利用传输矩阵算法绘制CFBG的反射谱和时延曲线，如图3所示。图3中啁啾光纤光栅反射谱和时延曲线存在明显的旁瓣纹，这源于光栅2端的Fabry-perot效应。对光纤光栅来说，如果谐振峰2边出现明显的波动，是不能用于通讯系统中进行色散补偿和滤波的，必须利用切趾技术来抑制光栅2端的Fabry-perot效应。

CFBG作为光信号的传输元件，其反射响应函数可以表示为：

R(ω)=r(ω)exp[iθ(ω)]

(9)

式中，R(ω)表示幅频响应； exp[iθ(ω)]表示相频响应。

将CFBG的响应函数相位θ(ω)展开为泰勒级数：

(10)

忽略更高阶色散，CFBG响应函数可以表示为：

(11)

3 基于CFBG的单边带调制

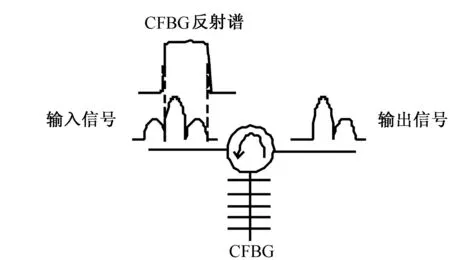
图4 啁啾光纤布拉格光栅滤波示意图

和常见的陷波滤波不同，对啁啾光栅，笔者在通带内选择一个边带和光载波，而滤掉另一个边带(见图4)。该方案正是利用了啁啾光栅大的反射带宽，它将光载波和一个边带反射并经光循环器进入光纤。另外，它还给光信号提供了色散预补偿，对传输中的光脉冲展宽有一定的抑制作用。

对于60G的调制系统，CFBG作为带通滤波器，反射带宽应该取0.96nm,光栅中心耦合波长应选择在1550.24nm或者1549.76nm附近，这样正好可以滤去一个边带而保留光载波和另外一个边带。光栅长度取8.5cm,有效折射率取1.46，啁啾系数取6×10-11nm/cm，有效折射率改变为0.00015，选择高斯切趾函数：

υ=e-16z2/L2

中心耦合波长设置在1550.24nm附近，ROF中高斯形载波光谱负载波调制的双边带谱见图5。

经过CFBG滤波调制后边带抑制比为22dB,载波衰减了2.3dB，信息边带几乎无衰减。单边带(SSB,Single Sideband)调制后的光谱结构见图6所示。

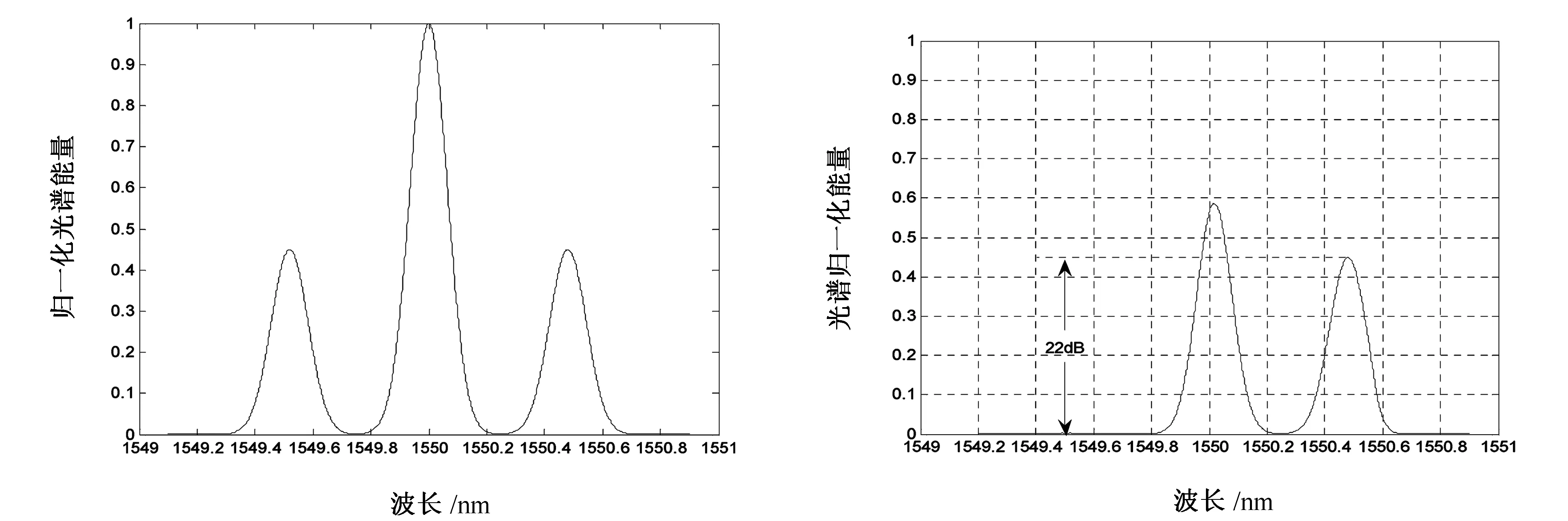
图5 高斯形负载波调制的双边带谱 图6 SSB调制谱结构

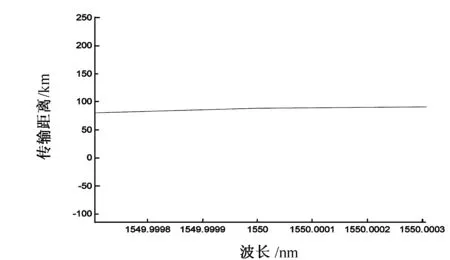
图7 CFBG色散补偿特性

对上述CFBG色散补偿作数值分析。在1550nm 窗口低阶色散|β2|约20ps2/km，可以求出1550nm附近CFBG补偿距离和波长的关系曲线(图7)，该曲线并非水平线，说明高阶色散的存在，计算得到该滤波光栅提供了88km的色散补偿。

4 结 语

利用CFBG带通滤波器，有效的抑制掉一个边带，实现光信息的单边带调制。同时CFBG带通滤波器对通带内传输的光脉冲给予色散补偿。另外，根据需要，适当的调整CFBG的参数，在满足较理想的边带抑制比的情况下，减少啁啾参数值可以实现更远的色散补偿距离。

[1]Graham H S, Dalma N, Zaheer A.Overcoming Chromatic-Dispersion Effects in Fiber-Wireless Systems Incorporating External Modulators[J]. Transactions On MicrowaveTheory And Chniques, 1997，45( 8)： 1410～1415.

[2]Park J, Sorin W V， Lau K Y. Elimination of the fibre chromatic dispersion penalty on 1550nm millimetre-wave optical transmission[J].Electron Lett, 1997,33(6),512～513.

[3]Shen Yichun, Zhang Xianmin, Chen Kangsheng. Optical Single Sideband Modulation of 11-GHz RoF System Using Stimulated Brillouin Scattering[J]. Photonics Technology Letters, 2005, 17(6),1277～1279.

[4]Elrefaie A F, Wagner R E, Atlas D A,etal.Chromatic dispersion limitations in coherent lightwave transmission systems[].IEEE J Lightwave Technol, 1988,6(5):704～709.

[5]Schmuck H.Comparison of optical millimetre-wave concepts with regard to chromatic dispersion[J].Electronics Letters, 1995,31(21):1848～1849.

[6]Erdogan Turan.Fiber Grating Spectr a[J].Journal of lightwave technology,1997,15(8):1277～1294.

[编辑] 洪云飞

O431.4

[MR(2000)主题分类号]78A50；78A55

A

1673-1409(2009)04-N015-03