探析数学例题教学的规律

沈　威　涂荣豹

数学是一门高度抽象的学科，为了让学生更好地建构数学概念的抽象意义，有的学者提出了“淡化形式，注重实质，的建议。由于数学自身的高度抽象性，即便是“淡化形式”之后的数学概念还是比较抽象，不容易理解。著名数学家G·波利亚说过“一个恰当的例题胜过一打理论。”表明教师在引导学生建构数学概念的时候，如果能够举出一个既揭示数学概念本质，又通俗易懂的例题，那么这个例题则胜过教师对概念“空对空”的很多遍重复解释。教师使用恰当的例题，能够降低其概念的抽象程度，突出概念的实质，有助于学生建构数学概念的意义。

数学教学的最重要任务，就是让学生以学习数学知识为载体，学习并掌握科学研究的一般方法。数学知识的学习不是对概念形式的空洞学习，而要以具体而浅显的实例来体现。学生在例题学习中不断地经历和感悟科学研究的一般方法，通过长时间的潜移默化，逐步成为学生自己的思考方式。然而，我们在研课过程中发现。教师向学生呈现以帮助他们建构数学概念的意义、掌握科学研究一般方法的例题中。还存在值得关注的问题。数学自身的特点和学生发展的需要决定了数学教学中，例题的选择和运用有其自身的特点和规律。本文正是遵循了“教与学对应”和“教与数学对应”二重原理的主旨，结合具体教学案例，探索在数学教学的不同情况下进行例题教学的一些规律。

一、复习旧知，引出新知

每节数学课的开始，教师让学生通过解决例题复习上一节课的相应知识，已经是我国数学课堂教学的主要方法。教师设计一个或几个具有代表性的例题，用于评价学生对上一节课知识的理解程度，并且通过例题，学生可以加深对相关知识的理解。同时，这些例题还有一个非常重要的作用：引出将要研究的新课题，或者引入某一个概念，或者为了推导一个公式。这基本符合人的认知规律，也与现代认知主义理论、建构主义思想一致。

案例1在正弦余弦函数的诱导公式上使用的例题。

师：今天的课题是正弦余弦的诱导公式，在前面学习中，我们学习了任意角三角函数的定义，就是说怎么求0°到90°的任意角的三角函数值，我们来看这个例题，这些角都不在0°到90°之间，那怎么去求它?大家自己求一下。

例1、求下列各三角函数的值：

(1)sin960°

(2)cos(-315°)

(3)sin(-30°)

(4)cos225°

(5)sin300°

(6)cos120°

教师和学生不停地讨论如何求这六个三角函数的值，此后才进入推导诱导公式的过程。

为研究新知，先复习旧知，不是让学生复述背诵纯记忆性的旧知，而是采用做例题的形式，对前一节课或几节课的学习内容进行复习、运用。用题目代替让学生单纯说出相关知识要有效得多，考察学生对“旧知”任意角的三角函数定义的理解程度，只需要选取具有代表性的例题为宜，难度不应过大。学生的回答可以反映出理解和迁移的具体情况，不需要选取很多的例题，因为在选取多个例题的情况下，学生需要时间把所有问题都解决，并且教师也需要时间作出评价，这就样消耗掉许多时间，不但占用了用于下面探究新知的时间，而且冲淡了本节课的主题，更影响了通过这些例题引出“新知”的功能。

本节课主要探究的内容是“正弦余弦函数的诱导公式”，但是为什么要探究“正弦余弦函数的诱导公式”?引导学生认识到探究“正弦余弦函数的诱导公式”的必要是这节课教学的主要任务之一。那么，如何启发学生认识到探究“正弦余弦的诱导公式”的必要性呢?我们认为使用“启发性提示语”可以达到这个目的，简单地说，“启发性提示语”不涉及具体认知的提问。而是关于元认知和方法论方面的提示语。例如“根据刚才例题，我们今天要研究什么内容?”“你打算怎么研究?”“你想从哪几个方面人手研究?”“接下来该怎么办?”“能不能向已知的转化?”“你的解题思路是什么?注意你的解题思路，”等等都是。这些问题提出后，不是教师来回答，而是仍然要由学生来解决，因此，教师又把问题交给学生去探索。这样就能够形成学生探究动机，启发学生驱动思维，在教师的引导下自然而然地引出新课的课题。

比如，可以让学生求sin960°和cos(-315°)的值对诱导公式一进行复习。通过对诱导公式一的复习，为新知“正弦余弦函数的诱导公式”的引出种下已有的“生长点”。由于上节课刚学习诱导公式一，所以学生很容易能够得到sin960°=sin(360°×2+240°)＝sin240°，在这个时候，可以用启发性提示语“接下来该怎么办?”“能不能向已知的转化?”提示学生，引导学生探究解决sin240°的方法“正弦余弦函数的诱导公式”。

学生不仅认识到研究“正弦余弦的诱导公式”的必要，体会“转化”是出于问题中刻画新数学对象的需要，而且还要经历“如何转化”的锻炼，有方法论意义，这样就在不知不觉中探究出了“正弦余弦的诱导公式”。不但经历了“研究目标”，而且经历了“研究方法”。这是一个“从无到有”的探究过程，对学生来说是一种挑战。因为这里所涉及的问题几乎都是原始的，“无限”开放的，这就充分体现“从无到有”的科学研究的一般方法、数学思维的本质以及数学理性精神。

二、巩固新知，深化认识

在数学课堂上，教师引导学生刚建构完一个新概念、新命题的意义之后，基本上都要向学生呈现相应的例题。通过例题教学达到对新概念、新命题吸收同化，简单运用，加深理解，把握要领的目的。

案例2在“平面与平面垂直”课上使用的例题

师：我们现在要判定两个面垂直有几种方法?

生：两种。

师：两种，一种是定义，最基本的。还有一个可以用它的判定定理。好，我们来做一个题。(演示题目)

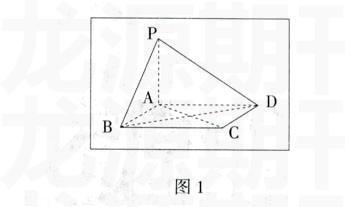
例2，如图l所示，四棱锥底面ABCD是正方形，PA上面ABCD。你能找到图中哪些面面垂直的位置关系?

在“平面与平面垂直”这节课中，重点之一是学生能够运用“平面与平面垂直的判定定理”解决简单问题。学生刚刚建构“平面与平面垂直的判定定理”的意义，在学生的认知结构中，“平面与平面垂直的判定定理”的意义还在进一步深化，在运用“平面与平面垂直的判定定理”的技能上，还不熟练，在选择例题的时候，应该选择简单的，容易理解的。

学生建构新概念、新命题意义的过程，并不是一次性完成的，而是持续不断地、逐渐地内化到其认知结构中。因此，学生在运用新概念、新命题的技能上的熟练程度也是逐步提高的，同样需要在不周的问题中不断地使用这些新概念、新命题逐渐达到自动化。新知学习后。例题的作用是帮助学生吸收同化，简单运用，加深理解，把握要领。那么解此题的要领是什么?一是直线垂直于平面，二是另一平面经过这条直线。只需数有几组线面垂直，再数每条垂线有几个平面经过，加起来除去重复的即可。所以

本题的答案是：1面PAD⊥面ABCD 2面PAB⊥面ABCD3面PAC⊥面ABCD 4面PAD⊥面PCD 5面PDB⊥面PAC 6面PAB⊥面PBC7面PCD⊥面PAD 8面PAB⊥面PAD。但是从后面对解题的分析来看，连教师都没达到相应的能力。很多问题与这个题类似，表面上例题涉及的知识学生已经具备，其实对知识的理解还差得远呢，而其所要求的能力，学生更是没有达到。因此对学生能力的要求不能过高，在巩固新概念的过程中呈现的例题，应该选择简单的，能够反映概念本质为宜，而不能选择像上述复杂程度和难度很高的例题。比如，另一位教师在这个位置为学生呈现的例题就比较合适：

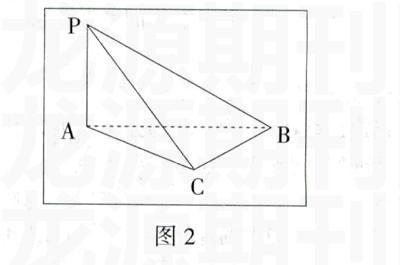
例3，已知：PA⊥平面ABC，AC⊥BC

求证：平面PAC⊥平面PBC。

三、探究未知，创造新知

新课程改革以来，对挖掘数学课堂例题潜能的尝试逐渐增加。对数学例题深层次问题的探究有利于巩固已学习的知识，加深对知识的理解，熟练解题技能，进而让学生经历创造的体验，养成创造的态度，培养创造的能力。

案例3人教版高中数学第二册(上)第七章“圆的一般方程”的例5

例4，已知一曲线是与两定点0(0，0)，A(3，0)距离的比为1/2的点的轨迹，求此曲线的方程，并画出曲线。

答案：(x+1)2+y2=4。方程的曲线是以C(-1，0)为圆心，2为半径的圆。

某老师利用人教版高中数学第二册(上)第七章“圆的一般方程”的例5，引导学生提出并探究了隐藏在该例题背后的4个深层次问题：

(1)将例题中的比值改为λ(λ＞0)，轨迹又是什么呢?

(2)将例题中的距离之比改为距离之积，轨迹又会是什么呢?

(3)若已知一圆，是否一定存在这样的两点，使圆上任一点到这两点的距离之比为同一个数呢?

(4)比值与圆的大小有什么必然的联系吗?

引导学生探究例题的未知，创造新知并不是一件容易的事，除对教师自身的要求较高外，对学生的要求也较高。由于探究未知对培养学生的可持续发展能力具有非常大的潜在价值，因此，引导学生对未知的探究还是非常必要的。即便在探究例题之后没有获得让人振奋的结论，但重要的是学生体验了创造。

探究例题背后隐藏未知问题之前，要解决这个例题。那么如何解决这个例题?首先要引导理解题意。清楚这是一个什么问题，即“它是什么?”然后进一步弄清“它有什么性质?”最后明白“它们有什么关系?这些关系怎么表示?”这些问题解决了，并且具有相应解题的技能和技巧把这些关系表达出来，才算解决了上述例题。首先要有解决这个例题的能力，才具备探究隐藏在例题背后未知问題的思考方式、策略和能力。

具备上述基础之后才能探究这个例题的未知部分。如何探究?是否有规律可寻?按照什么规律探究?还是按照科学研究的一般方法进行探究。就是启发学生以这个例题为背景，提出未知问题，也就是对问题进行猜想，形成新的问题，再进行解决。可以按照这样的启发性提示语引导学生探究例题：“条件一般化，能不能找到一个规律?”——即将例题中的比值改为λ(λ＞0)，轨迹又是什么呢?“修改例题中的某个条件，能不能找到一个规律?”——即把例题中的距离之比改为距离之积。轨迹又会是什么呢?“把已知的内容重新组织一下，能不能找出一个规律?”——即若已知一圆。是否一定存在这样的两点，使圆上任一点到这两点的距离之比为同一个数呢?和比值与圆的大小有什么必然的联系吗?“结论一般化，需要什么条件呢?”等等。当这些问题提出之后，又回到了解决问题的环节了，再次锻炼了学生的解题技巧和技能。从“理解题意”到“拟定计划”再到“解决问题”都是利用启发性提示语，在这个过程中，学生又一次受到科学研究的一般方法的训练和熏陶。重要的在于，这是一种解决新问题能力的培养和训练，实际上就是要从解决新问題的过程中学习如何解决新问题，培养和提高学生解决新问题的能力。引导学生探究新问题，是数学研究中的基本思想，也是数学学习的基本思考方式或策略。

数学教学一定要坚持科学研究的一般方法，例题教学是数学教学中的重要环节，例题教学应该是教学生获得一般科学方法的载体，而不是最终的目标。数学教学真正的最终目标应该是学生通过运用一般科学方法对数学知识的学习和探究，提高和发展他们的认识力。它的一个重要标志就是，学生能够不断地运用一般科学方法发现和提出各种新问题，并尝试用科学研究的一般方法解决这些新问题。发挥例题应有的价值是每一位数学教师的期待，只有充分把握例题教学的规律，才能完成数学例题教学的最终目标。

参考文献

[1]陈重穆，宋乃庆，淡化形式，注重实质，教学教育学报，1993(2).

[2]涂荣豹，数学教学认识论，南京：南京师范大学出版社，2004.

[3]涂荥豹，论数学教育研究的规范性，数学教育学报，2003(4).

[4]朱胜强，对一道解析几何例题的探究教学众学通报，2007(6).

(责任编辑付一静)