使用好初中数学新教材的两板斧

李志云

【摘 要】新的人教版初中数学教材在知识结构的编排上,是以螺旋上升的方式递进,在教材的处理上留给了教师很大的发展空间。经过两轮新课程的教学实践,对于如何使用新的数学教材,笔者从使用好初中数学新教材的两板斧谈谈心得体会。

【关键词】初中数学新教材 教材资源 思维能力

第一板斧:整合课本教材资源,创设认知与技能的最近发展区,促进学生数学学力的发展

新的教育理念要求教师不仅仅只是教材的使用者,更是教材的开发者。从教学实践效果来看,新版的人教版初中数学教材在编排上存在着一些不合理性,比如,教材编排上的缺陷问题、前后知识的顺序颠倒问题,等等。这些就需要我们教师在熟悉初中三年教材的基础上,认真研究,把一些教材资源重新整合,加以适当的补充,不断创造出一些知识上的最近发展区,从而有利于学生数学学力的形成与发展。

1.调整部分内容的顺序,符合学生的认知规律,扫除教学中的障碍

教材中有的内容在先后顺序上,存在着一定的不合理性,给教学带来某些障碍。比如,八年级下册的勾股定理与九年级上册的二次根式问题。因为二次根式的化简和运算都没有学过,因此,勾股定理的计算就不可能进行。现代认知心理学研究表明,要真正掌握、牢固记住某个新的知识点,不同的学生需要1次～20次不等的反复练习,才能贮存运用。可见,要掌握某个知识点离不开一定量的练习。要想真正掌握勾股定理的内容,离不开勾股定理的计算。

笔者在教学中是这样处理的,在八年级上册讲授开平方时,就把二次根式的运算提前在这里讲解,效果比较好。一来学生对开平方理解的更加透彻,简单的开方运算不会出差错;二来在学习勾股定理时,学生就不会存在计算上的障碍,勾股定理深层次的运用能顺利进行。

2.组合教材正文与课后阅读观察,激发学生的思维能力,促进学生的可持续发展能力的形成

笔者根据后继学习内容的需要,考虑到学生在学习上的可持续发展,我们可以将教材后面的拓展内容(观察与阅读部分)与教材正文部分有机的联系起来进行教学。例如,在七年级下册因式分解这一节,我把教材后的观察与思考中的x2+(p+q)x+pq型的因式分解放在公式法后让学生研究。

在教学中,我通过设计问题情境组来开拓学生的思维空间。设计了这样几个步骤:①回忆因式分解的两种方法,并说说因式分解与整式乘法的区别与联系;②计算式子:(x+p)(x+q);③试试看,把式子x2+(p+q)x+pq因式分解;④因式分解下列式子:⑴x2-3x+2,⑵x2+5x+6。这样设计,是建立在学生对整式乘法与因式分解区别与联系已知的基础上进行的,既复习了前面内容,又发展了学生的思维能力,促进了学生数学学力的发展,同时通过第④问的练习,让学生又一次体验到自主获取知识的成就感。

这样处理,既给学生带来一种新的解题方法,拓广了解题思路,又便于学生在八年级下册的分式化简、九年级上册的一元二次方程的求解时能得心应手,提高解题速度和正确率。

3.根据知识内容的重要性,及时糸统的补充相关数学知识,弥补教材带来的缺陷

字母表示数是学生认识上的一个飞跃,本身就是数学教学上的一个难点。用字母表示数这一内容,新教材没有单独作为一节列出来讲授,但是在教学中又时不时的碰到它,比如,从初一年级开始练习中就有找规律,用字母表示出一般规律;教材中有合并的概念,涉及到字母合并问题;解一元一次方程,等等。很多学生存在着这样一个共同的问题,那就是对于纯数字运算的题目解答时能得心应手,而碰到含有字母的题目解答时就觉得疙里疙瘩。我认为,这是没有糸统讲授字母表示数这一内容造成的,也可以说,是新人教版教材在编写上的一大缺陷。

鉴于字母表示数在学生学习过程中的重要性,有必要拿出一定时间进行糸统地讲解,让学生知道字母表示数的意义,亲自经历字母表示数的过程,逐渐建立字母表示数的模型,从而熟练运用字母表示数。

第二板斧:从不同角度开发课本典型例题、习题,训练学生的思维能力,提高教学的有效性

新课程改革一个重要目标就是减轻学生的作业负担,提高学生的思维能力。就数学这门学科而言,减轻负担就是要杜绝题海战术。那么怎样通过适量的训练,就能达到事半功倍的效果呢?我们可以从不同的角度开发课本典型的例题、习题,提高教学的有效性。

课本上的例题、习题中的许多题目具有典型性,简明扼要,难度适当,面向大多数学生,是巩固课堂所学知识必不可少的内容。如果我们平时能有意识的加以探究与拓展,就一定能取得很大的教学效益,下面,以九年级上册P103页第14题为例加以说明。

题目:如图1,已知AB是⊙O直径,C为⊙O上

一点,AD和过C点的切线垂直,垂足为D.

求证:AC平分∠DAB.

1.从解法上进行挖掘,培养思维的发散性

从解法上进行挖掘就是进行一题多解,就是

引导学生对同一条件用各种途径、多种方法思考问题,探求不同的解答方案。这样,既可暴露学生解题的思维过程,又能够拓广学生的思路,培养思维的发散性。

本题的证法一:可以连结BC,利用直径所对圆圈角是直角,再弦切角定理和互余性质得证。证法二:可以连结OC,借助切线的性质、平行线的性质、等边对等角得以证明。

2.从结论上进行拓展,培养思维的灵活性从结论上进行拓展,就是条件不变情况下挖掘新的结论,或把原题中的条件适当增减得出原有结论或新结论,或是把原题条件与结论互换看是否还成立。这样能使学生随时根据变化了的情况积极思索,设法想出解决的办法,从而防止和消除呆板和僵化,培养思维的灵活性。

本题可以在条件不变的基础上,结论改为求证∠BAD=2∠BAC;学了三角形相似后可以改为求证AC2=AD•AB。可以将结论中AC平分∠DAB与条件中的DC是切线互换,其余不变,判断新命题是否成立(这里仍成立)。

3.从图形上进行延伸,培养思维的深刻性

从图形上进行延伸就是把原图形进行适当的变形,条件相应的进行微小变化。从表面上看与原题有区别,但实质上结构却是相同的,因而它们可用同一种思路去解答。通过这样的题组作比较,可使学生透过表面现象,自觉地从本质上看问题,从而培养思维的深刻性。

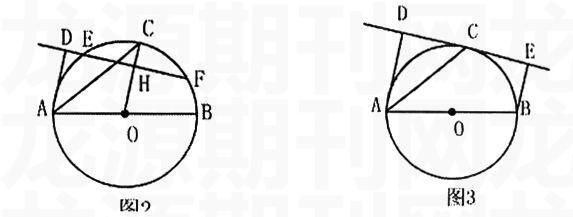
本题可以将切线DC向下平移,变为割线DEF,如图2所示,H为EF的中点,其余条件不变,求证原题结论。本题解法与原题解法2类似,多了一个证明OH⊥EF的过程。

也可以在条件中添加BE⊥CD,垂足为E,如图3,其余不变,求证:⑴AC平分∠DAB ;⑵ AD+BE=AB。

第⑴问解答与原题一样,第⑵问连接OC之后,由梯形中位线结论得到AD+BE=2OC,AB=2OC,从而结论得证。

总之,在数学教学过程中,从不同角度开发课本例题、习题,有意识地把教学过程体现为数学思维活动的过程,就能充分调动学生的积极性、主动性,可以使学生在全面、深刻的理解和掌握知识的同时,思维品质也获得良好的发展。