活动的设计促使知识“自然”产生

马翠英

平面直角坐标系的教学设计是:先确定学校的位置,通过方位图形引入平面直角坐标系,然后分析用有序数对表示位置。

教学过程:

一、提出问题——怎样确定位置

活动1:很多小学生慕名我们学校(实验中学),你能为他们描述一下我们学校的位置吗?还有实验中学分校的位置?

先让学生个别思考,再进行合作交流,然后小组代表阐述方法或不同意见。

组1:乘88路公交车到九州商厦下车,对面就是实验中学。

组2:只要到九州商厦的公交车都行。

组3:内蒙古医院往北200米路西就是。内蒙古医院十字路口往西100米,再往北200米就是实验中学分校。

组4:昭乌达路75号。

组5:我是用图形表示的。

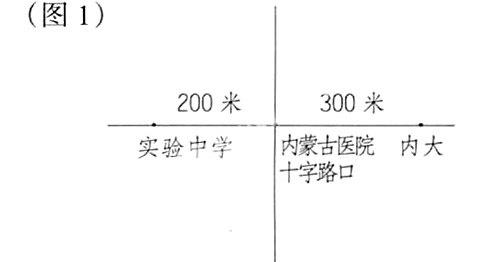
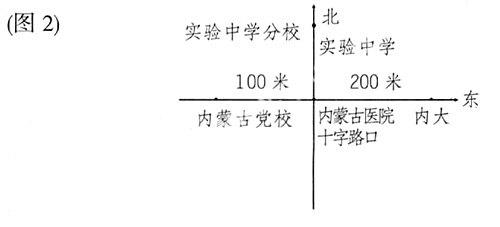
组6:我们也是用图形表示的,但比5组好。(图2)因为地图册里表示地理位置是上北下南,左西右东。

师:第6组同学的想法很好;和地图册里表示地理位置的方法一致,将实际问题的位置表示图形化了。

每组代表回答后我都没给出评价,让他们尽可能地把所有想法都说出来。

活动1的设计意图是让学生感受定位方法,明确定位方法的多样性及图形表示位置的直观性,为进一步抽象概括奠定基础。

二、解决问题——建立平面直角坐标系

活动2:同学们能否用数学的方法更简捷地表示实验中学的位置?

先让学生个别思考,然后进行合作交流。

组1:实验中学可以表示为200。

组2:不同意,内蒙古医院十字路口往南200米有其他单位。

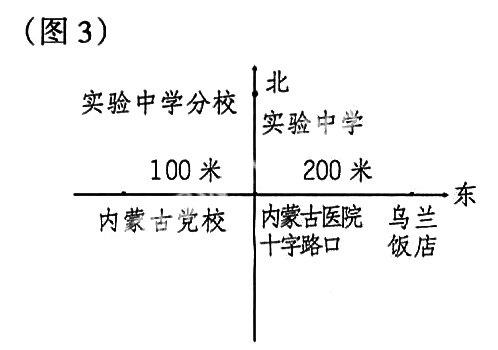
组3:把内蒙古医院十字路口定为原点O,向(图3)北为正,用+200,向南用-200。

师:非常好,正负数就是表示具有相反意义的量。那向东200米的乌兰饭店怎样表示呢?

组4:东和西又是相反的方向,我们把向东规定为正方向,那么乌兰饭店就是向东+200。

这样,规定了正方向后,一个平面直角坐标系浮在眼前。

师:大家不得了,这样表示位置的方法是当年笛卡儿发现的。说明同学们有当数学家的潜质。

(大家情绪高涨)

1.简介笛卡儿:

笛卡儿是17世纪法国杰出的哲学家、是近代生物学的奠基人、是当时世界一流的物理学家。并不是数学家,但直角坐标系的发现使他成为当之无愧的现代数学的创始人之一。

2.什么是平面直角坐标系?阅读课本41页倒数第二段,认识平面直角坐标系的相关概念,(在图3中标出X轴、Y轴、原点)

活动2的设计意图是帮助学生把生活经验上升为数学模型,让学生经历用数学符号、图形描述现实世界的过程。

三、深化问题——认识坐标(有序数对)

活动3:提出问题

(1) 能否用数表示实验中学、实验中学分校、乌兰饭店、内蒙古党校的位置?借机介绍坐标。

(2)满族小学的坐标(-100,400),你能在图中找出它的位置吗?

(3)实验中学坐标(0,200)和乌兰饭店坐标(200,0)一样吗?

(4)内蒙古医院十字路口的坐标如何表示?

活动3的设计意图是让学生掌握在平面直角坐标系中,已知点求坐标和已知坐标描点的技能,领悟平面上点与有序数对一一对应的关系。

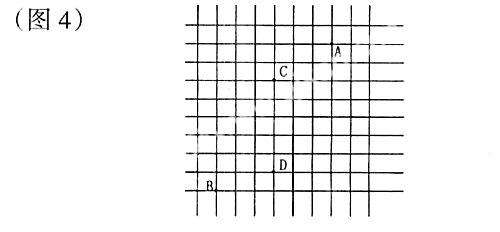
活动4:完成课本41页思考:(图4)你能不能表示图4中A、B、C、D、各点的坐标?

生:没法表示,因为没有平面直角坐标系。

建立坐标系并标出坐标后,同桌互相检查:平面直角坐标系的元素是否标齐?在自己建立平面直角坐标系下坐标是否正确?

活动4的设计意图是(1)训练学生自己建立平面直角坐标系的意识。(2)选择不同的平面直角坐标系坐标不同,但不影响总的相对位置。

四、应用问题——有序数对在生活中的实例

生活中也经常利用有序数对来表示位置。

假如我们规定列在前,行在后,你能用有序数对说出你的座位吗?今天我们换个称呼,不叫姓名,叫你的坐标。

活动5:生活中还有哪些问题利用有序数对来表示位置的?

如进电影院找座位是几排几号、棋盘中棋子的位置、课程表中某一天的课程、值日表、运动会的翻牌、电子字幕、地理中经纬度是平面直角坐标系在球面上的运用等。

活动5的设计意图是通过实例进一步认识坐标和有序数对。

五、归纳总结——深化知识

活动6:谈谈你学习本节课的收获:

生1:数学知识来源于实际生活。

生2:数学符号太简洁了。

生3:数学太神奇、笛卡儿太伟大了。

活动6的设计意图是使学生对本课所学的知识有一个清晰的认识,对本课所用的思想方法有一个明确的了解。

师强调:

1.实际问题到数学问题再到实际问题;

2.文字语言到图形语言再到符号语言;

3.数形结合的数学思想和方法

许多数学家普遍认为笛卡儿的直角坐标系不同于一般的数学理论,它是一种数学思想和方法,它的发明将代数与几何有机地结合在一起,在此之前的一千多年里数和形是分离的。

恩格斯把平面直角坐标系称为数学的转折点;华罗庚说:“数缺形时少直觉;形缺数时难入微。”这是对笛卡儿的最高评价。

教后反思:

笛卡儿躺在床上看到飞着的苍蝇,就想怎样确定它的位置?进而诞生了这个伟大的发现。然而“使世界震惊的是让笛卡儿看到,利用他的坐标系,平面上每一点都可以用两个数的有序组来表示。”所以我的教学设计就体现了知识的产生过程,学生仿佛置身于笛卡儿当年的探索情境中。从确定学校的位置的活动中,由用语言描述到用图形表示,又结合表示相反意义的量将互相垂直的两条路(乌兰察布路和昭乌达路)自然转变为两条互相垂直的数轴,平面直角坐标系孕育而生。

这样将“有序数对”、“平面直角坐标系”“用坐标表示地理位置”3节课并为1节课,节省了教学时间,提升了课堂效率。