概率与统计高考命题趋势与指导

都述利

一、设计背景

《2006年普通高等学校招生全国统一考试大纲》（理科数学新课程版）明确指出：“对数学基础知识的考查，要求全面又突出重点，对于支撑学科知识体系的重点知识，考查时要保持较高的比例，构成数学试题的主体.”由于新课程新增内容大都接近现代数学的重要基础，无论对于学生今后的进一步学习，还是对于激发学生对于数学学科的学习兴趣、增强学生的数学应用意识，都具有十分重要的意义.因此他们必然成为支撑数学学科知识体系的重点知识，从而成为保持较高比例，构成数学试题的主体知识的重要板块.

《概率与统计》是一门“研究偶然现象统计规律性”的学科.随着科学技术的发展，概率和统计这门“研究偶然现象统计规律性”的学科在社会生活实际以及科学实验和研究中都得到了越来越广泛的应用.基于以上原因，新课程增加了概率和统计基础知识的相关内容.近几年来，新课程高考试卷也把概率和统计的基础知识和方法——随机事件、等可能事件、互斥事件、相互独立事件、独立重复试验等概率及相应的计算和离散型随机变量分布列和数学期望等概念和计算列为考查的重点，作为必考内容.因此高考就利用概率与统计知识设计试题来考查学生的应用意识、实践能力；考查学生的分析问题和解决问题的能力；考查学生的分类讨论思想、等价转化思想以及对背景新奇问题的理解中所表现出来的不同思维品质、思维能力.

该专题将从概率与统计的基础知识着手，根据高考要求进行设计，既紧扣主干知识，又突出重点，同时注重数学教学实际.

二、高考考点回顾

在2004~2009年全国新课程卷高考试题中每年都有出现1~2道概率与统计试题，所占分数在12~16分之间，具体考查知识点如下表所示：

三、考点知识结构及分析

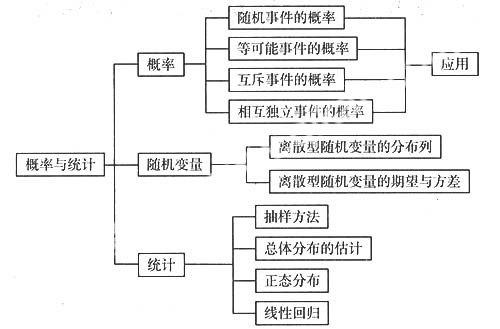
概率与统计重点考查的内容是利用等可能性事件、互斥事件和相互独立事件等概率的计算求某些简单的离散型随机变量的分布列、期望与方差，及根据分布列求事件的概率.用样本方差去估计总体方差，用样本频率分布估计总体分布，用样本频率分布求其累积频率分布等的计算问题.应用概率与统计知识要解决的题型主要分两大类，一类是应用随机变量的概念，特别是离散型随机变量分布列及期望与方差的基础知识，讨论随机变量的取值范围，取相应值得概率及期望、方差的求解计算；另一类主要是如何抽取样本及如何用样本去估计总体.

四、命题趋向预测

1.概率统计命题特点.在近五年高考中,每年都有一道概率统计解答题实施新课标考试的省份,增加到两道客观题和一道解答题．

值得一提的是，此类试题体现了考试中心提出的“突出应用能力考查”以及“突出新增加内容的教学价值和应用功能”的指导思想.在命题时,提高了分值和难度,并设置了灵活的题目情境.

就考查内容而言,用概率定义或基本事件求事件概率，常以小题形式出现，随机变量取值——取每一个值的概率——列分布列——求期望方差常以大题形式出现．

2.考点透视.

（1）了解随机事件的发生存在着规律性和随机事件概率的意义．

（2）了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率.

（3）了解互斥事件、相互独立事件的意义，会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率．

（4）会计算事件在n次独立重复试验中恰好发生k次的概率．

（5）掌握离散型随机变量的分布列.

（6）掌握离散型随机变量的期望与方差.

（7）掌握抽样方法与总体分布的估计.

（8）掌握正态分布与线性回归.